|
Exchangeable Random Variables
In statistics, an exchangeable sequence of random variables (also sometimes interchangeable) is a sequence ''X''1, ''X''2, ''X''3, ... (which may be finitely or infinitely long) whose joint probability distribution does not change when the positions in the sequence in which finitely many of them appear are altered. Thus, for example the sequences : X_1, X_2, X_3, X_4, X_5, X_6 \quad \text \quad X_3, X_6, X_1, X_5, X_2, X_4 both have the same joint probability distribution. It is closely related to the use of independent and identically distributed random variables in statistical models. Exchangeable sequences of random variables arise in cases of simple random sampling. Definition Formally, an exchangeable sequence of random variables is a finite or infinite sequence ''X''1, ''X''2, ''X''3, ... of random variables such that for any finite permutation σ of the indices 1, 2, 3, ..., (the permutation acts on only finitely many indices, with the res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Large Numbers
In probability theory, the law of large numbers (LLN) is a theorem that describes the result of performing the same experiment a large number of times. According to the law, the average of the results obtained from a large number of trials should be close to the expected value and tends to become closer to the expected value as more trials are performed. The LLN is important because it guarantees stable long-term results for the averages of some random events. For example, while a casino may lose money in a single spin of the roulette wheel, its earnings will tend towards a predictable percentage over a large number of spins. Any winning streak by a player will eventually be overcome by the parameters of the game. Importantly, the law applies (as the name indicates) only when a ''large number'' of observations are considered. There is no principle that a small number of observations will coincide with the expected value or that a streak of one value will immediately be "balanced ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC, pronounced ) ― also known as Pearson's ''r'', the Pearson product-moment correlation coefficient (PPMCC), the bivariate correlation, or colloquially simply as the correlation coefficient ― is a measure of linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of teenagers from a high school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Urn Model
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems.Dodge, Yadolah (2003) ''Oxford Dictionary of Statistical Terms'', OUP. History In ''Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the ''inverse probability'' problem, and was a topic of res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixture Distribution
In probability and statistics, a mixture distribution is the probability distribution of a random variable that is derived from a collection of other random variables as follows: first, a random variable is selected by chance from the collection according to given probabilities of selection, and then the value of the selected random variable is realized. The underlying random variables may be random real numbers, or they may be random vectors (each having the same dimension), in which case the mixture distribution is a multivariate distribution. In cases where each of the underlying random variables is continuous, the outcome variable will also be continuous and its probability density function is sometimes referred to as a mixture density. The cumulative distribution function (and the probability density function if it exists) can be expressed as a convex combination (i.e. a weighted sum, with non-negative weights that sum to 1) of other distribution functions and density function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
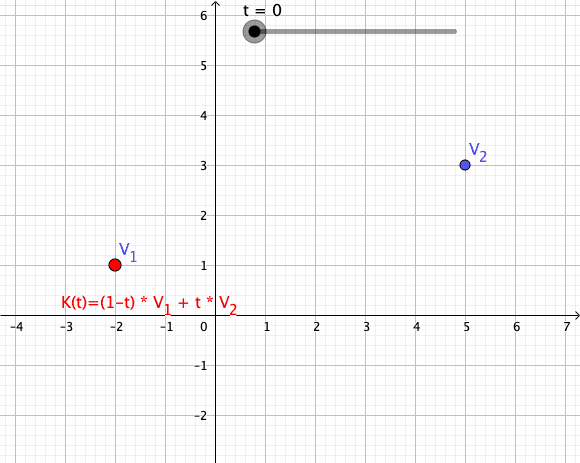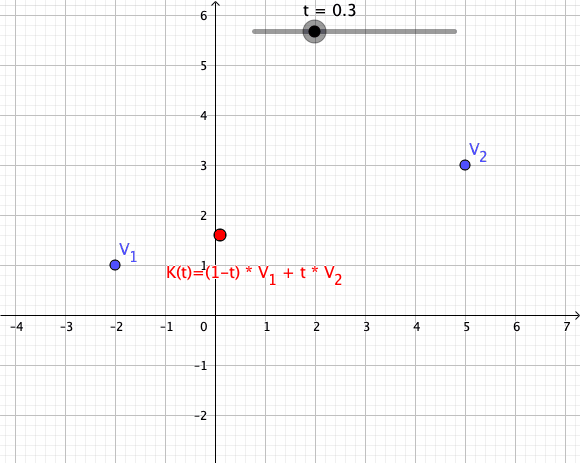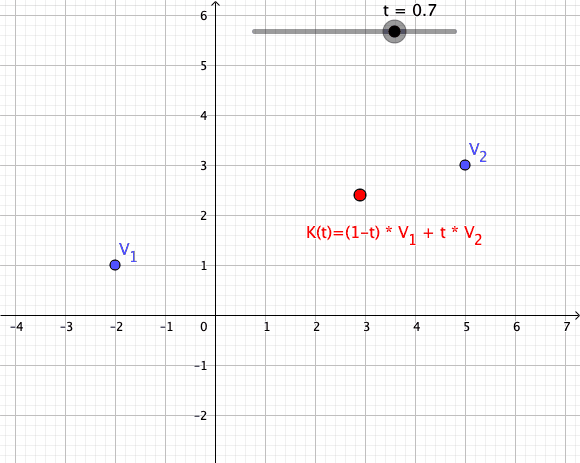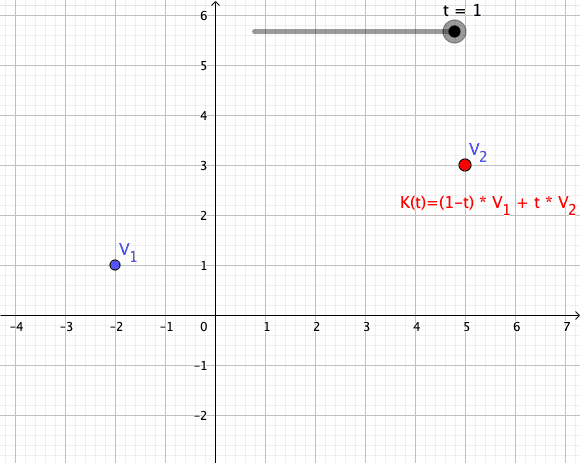
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Banach Limit
In mathematical analysis, a Banach limit is a continuous linear functional \phi: \ell^\infty \to \mathbb defined on the Banach space \ell^\infty of all bounded complex-valued sequences such that for all sequences x = (x_n), y = (y_n) in \ell^\infty, and complex numbers \alpha: # \phi(\alpha x+y) = \alpha\phi(x) + \phi(y) (linearity); # if x_n\geq 0 for all n \in \mathbb, then \phi(x) \geq 0 (positivity); # \phi(x) = \phi(Sx), where S is the shift operator defined by (Sx)_n=x_ (shift-invariance); # if x is a convergent sequence, then \phi(x) = \lim x . Hence, \phi is an extension of the continuous functional \lim: c \to \mathbb C where c \subset\ell^\infty is the complex vector space of all sequences which converge to a (usual) limit in \mathbb C. In other words, a Banach limit extends the usual limits, is linear, shift-invariant and positive. However, there exist sequences for which the values of two Banach limits do not agree. We say that the Banach limit is not uniquely determ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cesaro Summation
Cesaro may refer to: * Cesarò, a town in Italy * Cesaro (wrestler) (Claudio Castagnoli, born 1980), a Swiss wrestler * Andrea Cesaro (born 1986), an Italian footballer * Ernesto Cesàro (1859–1906), an Italian mathematician **Cesàro equation **Cesàro summation In mathematical analysis, Cesàro summation (also known as the Cesàro mean ) assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as ''n'' tends to infinity, of ... See also * {{disambiguation, surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Distribution Function
In statistics, an empirical distribution function (commonly also called an empirical Cumulative Distribution Function, eCDF) is the distribution function associated with the empirical measure of a sample. This cumulative distribution function is a step function that jumps up by at each of the data points. Its value at any specified value of the measured variable is the fraction of observations of the measured variable that are less than or equal to the specified value. The empirical distribution function is an estimate of the cumulative distribution function that generated the points in the sample. It converges with probability 1 to that underlying distribution, according to the Glivenko–Cantelli theorem. A number of results exist to quantify the rate of convergence of the empirical distribution function to the underlying cumulative distribution function. Definition Let be independent, identically distributed real random variables with the common cumulative distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequentist Statistics
Frequentist inference is a type of statistical inference based in frequentist probability, which treats “probability” in equivalent terms to “frequency” and draws conclusions from sample-data by means of emphasizing the frequency or proportion of findings in the data. Frequentist-inference underlies frequentist statistics, in which the well-established methodologies of statistical hypothesis testing and confidence intervals are founded. History of frequentist statistics The history of frequentist statistics is more recent than its prevailing philosophical rival, Bayesian statistics. Frequentist statistics were largely developed in the early 20th century and have recently developed to become the dominant paradigm in inferential statistics, while Bayesian statistics were invented in the 19th century. Despite this dominance, there is no agreement as to whether frequentism is better than Bayesian statistics, with a vocal minority of professionals studying statistical infer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |