|
Euler's Gem
''Euler's Gem: The Polyhedron Formula and the Birth of Topology'' is a book on the formula V-E+F=2 for the Euler characteristic of convex polyhedra and its connections to the history of topology. It was written by David Richeson and published in 2008 by the Princeton University Press, with a paperback edition in 2012. It won the 2010 Euler Book Prize of the Mathematical Association of America. Topics The book is organized historically, and reviewer Robert Bradley divides the topics of the book into three parts. The first part discusses the earlier history of polyhedra, including the works of Pythagoras, Thales, Euclid, and Johannes Kepler, and the discovery by René Descartes of a polyhedral version of the Gauss–Bonnet theorem (later seen to be equivalent to Euler's formula). It surveys the life of Euler, his discovery in the early 1750s that the Euler characteristic V-E+F is equal to two for all convex polyhedra, and his flawed attempts at a proof, and concludes with the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by \chi ( Greek lower-case letter chi). The Euler characteristic was originally defined for polyhedra and used to prove various theorems about them, including the classification of the Platonic solids. It was stated for Platonic solids in 1537 in an unpublished manuscript by Francesco Maurolico. Leonhard Euler, for whom the concept is named, introduced it for convex polyhedra more generally but failed to rigorously prove that it is an invariant. In modern mathematics, the Euler characteristic arises from homology and, more abstractly, homological algebra. Polyhedra The Euler characteristic \chi was classically defined for the surfaces of polyhedra, acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré–Hopf Theorem
In mathematics, the Poincaré–Hopf theorem (also known as the Poincaré–Hopf index formula, Poincaré–Hopf index theorem, or Hopf index theorem) is an important theorem that is used in differential topology. It is named after Henri Poincaré and Heinz Hopf. The Poincaré–Hopf theorem is often illustrated by the special case of the hairy ball theorem, which simply states that there is no smooth vector field on an even-dimensional n-sphere having no sources or sinks. Formal statement Let M be a differentiable manifold, of dimension n, and v a vector field on M. Suppose that x is an isolated zero of v, and fix some local coordinates near x. Pick a closed ball D centered at x, so that x is the only zero of v in D. Then the index of v at x, \operatorname_x(v), can be defined as the degree of the map u : \partial D \to \mathbb S^ from the boundary of D to the (n-1)-sphere given by u(z)=v(z)/\, v(z)\, . Theorem. Let M be a compact differentiable manifold. Let v be a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seifert Surface
In mathematics, a Seifert surface (named after German mathematician Herbert Seifert) is an orientable surface whose boundary is a given knot or link. Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface. Seifert surfaces are also interesting in their own right, and the subject of considerable research. Specifically, let ''L'' be a tame oriented knot or link in Euclidean 3-space (or in the 3-sphere). A Seifert surface is a compact, connected, oriented surface ''S'' embedded in 3-space whose boundary is ''L'' such that the orientation on ''L'' is just the induced orientation from ''S''. Note that any compact, connected, oriented surface with nonempty boundary in Euclidean 3-space is the Seifert surface associated to its boundary link. A single knot or link can have many different inequivalent Seifert surfaces. A Seifert surface must be oriented. It is possible t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In the mathematical field of topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, Unknot, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3 (in topology, a circle is not bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of descr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orientability
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classification Of Manifolds
In mathematics, specifically geometry and topology, the classification of manifolds is a basic question, about which much is known, and many open questions remain. Main themes Overview * Low-dimensional manifolds are classified by geometric structure; high-dimensional manifolds are classified algebraically, by surgery theory. : "Low dimensions" means dimensions up to 4; "high dimensions" means 5 or more dimensions. The case of dimension 4 is somehow a boundary case, as it manifests "low dimensional" behaviour smoothly (but not topologically); see discussion of "low" versus "high" dimension. * Different categories of manifolds yield different classifications; these are related by the notion of "structure", and more general categories have neater theories. * Positive curvature is constrained, negative curvature is generic. * The abstract classification of high-dimensional manifolds is ineffective: given two manifolds (presented as CW complexes, for instance), there is no algorithm t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poul Heegaard
Poul Heegaard (; November 2, 1871, Copenhagen - February 7, 1948, Oslo) was a Danish mathematician active in the field of topology. His 1898 thesis introduced a concept now called the Heegaard splitting of a 3-manifold. Heegaard's ideas allowed him to make a careful critique of work of Henri Poincaré. Poincaré had overlooked the possibility of the appearance of torsion in the homology groups of a space. He later co-authored, with Max Dehn, a foundational article on combinatorial topology, in the form of an encyclopedia entry. Heegaard studied mathematics at the University of Copenhagen, from 1889 to 1893 and following years of travelling, and teaching mathematics, he was appointed professor at University of Copenhagen in 1910. An English translation of his 1898 thesis, which laid a rigorous topological foundation for modern knot theory, may be found at https://www.maths.ed.ac.uk/~v1ranick/papers/heegaardenglish.pdf. The section on "a visually transparent representation of the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Dehn
Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Born to a Jewish family in Germany, Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States. Dehn was a student of David Hilbert, and in his habilitation in 1900 Dehn resolved Hilbert's third problem, making him the first to resolve one of Hilbert's well-known 23 problems. Dehn's students include Ott-Heinrich Keller, Ruth Moufang, Wilhelm Magnus, and the artists Dorothea Rockburne and Ruth Asawa. Biography Dehn was born to a family of Jewish origin in Hamburg, Imperial Germany. He studied the foundations of geometry with Hilbert at Göttingen in 1899, and obtained a proof of the Jordan curve theorem for polygons. In 1900 he wrote his dissertation on the role of the Legendre angle sum theorem in axiomatic geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernhard Riemann
Georg Friedrich Bernhard Riemann (; 17 September 1826 – 20 July 1866) was a German mathematician who made contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the first rigorous formulation of the integral, the Riemann integral, and his work on Fourier series. His contributions to complex analysis include most notably the introduction of Riemann surfaces, breaking new ground in a natural, geometric treatment of complex analysis. His 1859 paper on the prime-counting function, containing the original statement of the Riemann hypothesis, is regarded as a foundational paper of analytic number theory. Through his pioneering contributions to differential geometry, Riemann laid the foundations of the mathematics of general relativity. He is considered by many to be one of the greatest mathematicians of all time. Biography Early years Riemann was born on 17 September 1826 in Breselenz, a village near Dannenb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
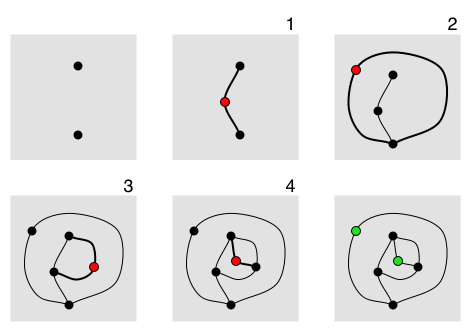
Sprouts (game)
Sprouts is a paper-and-pencil game which can be analyzed for its mathematical properties. It was invented by mathematicians John Horton Conway and Michael S. Paterson at Cambridge University in the early 1960s. The setup is even simpler than the popular Dots and Boxes game, but game-play develops much more artistically and organically. Rules The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules. * The line may be straight or curved, but must not touch or cross itself or any other line. * The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines. * No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself cou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Game Theory
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a ''position'' that the players take turns changing in defined ways or ''moves'' to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |