|
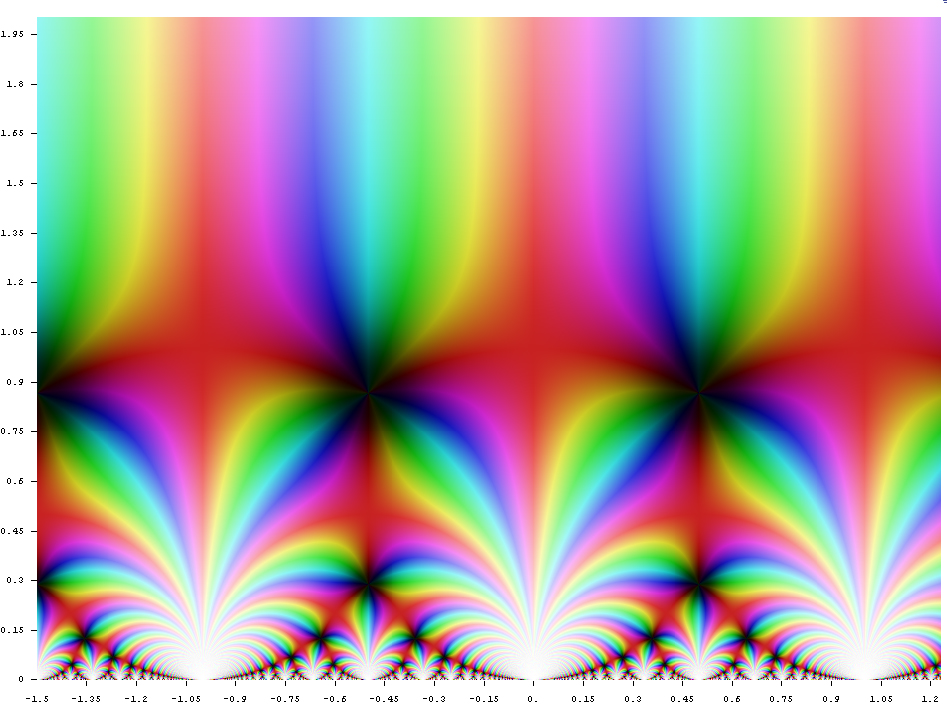
Elliptic Modular Function
In mathematics, Felix Klein's -invariant or function, regarded as a function of a complex variable , is a modular function of weight zero for defined on the upper half-plane of complex numbers. It is the unique such function which is holomorphic away from a simple pole at the cusp such that :j\left(e^\right) = 0, \quad j(i) = 1728 = 12^3. Rational functions of are modular, and in fact give all modular functions. Classically, the -invariant was studied as a parameterization of elliptic curves over , but it also has surprising connections to the symmetries of the Monster group (this connection is referred to as monstrous moonshine). Definition The -invariant can be defined as a function on the upper half-plane :j(\tau) = 1728 \frac = 1728 \frac = 1728 \frac with the third definition implying j(\tau) can be expressed as a cube, also since 1728 = 12^3. The given functions are the modular discriminant \Delta(\tau) = g_2(\tau)^3 - 27g_3(\tau)^2 = (2\pi)^\,\eta^(\tau) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1728 (number)
1728 is the natural number following 1727 and preceding 1729. 1728 is a dozen gross, one great gross (or grand gross). It is the number of cubic inches in a cubic foot. It is also the number of daily chants of the Hare Krishna mantra by a Hare Krishna devotee. The number comes from 16 rounds on a 108 japamala bead. In mathematics 1728 is the cube of 12 and, as such, is important in the duodecimal number system, in which it is represented as "1000". * 1728 = 123 * 1728 = 33 × 43 * 1728 = 23 × 63 * 1728 = 63 + 83 + 103 * 1728 = 242 + 242 + 242 * 1728 = 2893 + 2873 + (−288)3 + (−288)3 * 28 divisors: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48, 54, 64, 72, 96, 108, 144, 192, 216, 288, 432, 576, 864, 1728 1728 is the number of directed open knight's tours on a chessboard. 1728 occurs in the algebraic formula for the j-invariant of an elliptic curve, as a function over a complex variable on the upper half-plane \,\mathcal : \, :j(\tau) = 1728 \frac = 1728 \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Special Linear Group
In mathematics, especially in the group theoretic area of algebra, the projective linear group (also known as the projective general linear group or PGL) is the induced action of the general linear group of a vector space ''V'' on the associated projective space P(''V''). Explicitly, the projective linear group is the quotient group :PGL(''V'') = GL(''V'')/Z(''V'') where GL(''V'') is the general linear group of ''V'' and Z(''V'') is the subgroup of all nonzero scalar transformations of ''V''; these are quotiented out because they act trivially on the projective space and they form the kernel of the action, and the notation "Z" reflects that the scalar transformations form the center of the general linear group. The projective special linear group, PSL, is defined analogously, as the induced action of the special linear group on the associated projective space. Explicitly: :PSL(''V'') = SL(''V'')/SZ(''V'') where SL(''V'') is the special linear group over ''V'' and SZ(''V'') is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Group
In mathematics, the modular group is the projective special linear group of matrices with integer coefficients and determinant 1. The matrices and are identified. The modular group acts on the upper-half of the complex plane by fractional linear transformations, and the name "modular group" comes from the relation to moduli spaces and not from modular arithmetic. Definition The modular group is the group of linear fractional transformations of the upper half of the complex plane, which have the form :z\mapsto\frac, where , , , are integers, and . The group operation is function composition. This group of transformations is isomorphic to the projective special linear group , which is the quotient of the 2-dimensional special linear group over the integers by its center . In other words, consists of all matrices :\begin a & b \\ c & d \end where , , , are integers, , and pairs of matrices and are considered to be identical. The group operation is the usual mult ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Form
In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the Group action (mathematics), group action of the modular group, and also satisfying a growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology, sphere packing, and string theory. A modular function is a function that is invariant with respect to the modular group, but without the condition that be Holomorphic function, holomorphic in the upper half-plane (among other requirements). Instead, modular functions are Meromorphic function, meromorphic (that is, they are holomorphic on the complement of a set of isolated points, which are poles of the function). Modular form theory is a special case of the more general theory of automorphic form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass's Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Definition Let \omega_1,\omega_2\in\mathbb be two complex numbers that are linearly independent over \mathbb and let \Lambda:=\mathbb\omega_1+\mathbb\omega_2:=\ be the lattice generated by those numbers. Then the \wp-function is defined as follows: \weierp(z,\omega_1,\omega_2):=\weierp(z,\Lambda) := \frac + \sum_\left(\frac 1 - \frac 1 \right). This series converges locally uniformly absolutely in \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of the polynomial . That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number 1 + i is algebraic because it is a root of . All integers and rational numbers are algebraic, as are all roots of integers. Real and complex numbers that are not algebraic, such as and , are called transcendental numbers. The set of algebraic numbers is countably infinite and has measure zero in the Lebesgue measure as a subset of the uncountable complex numbers. In that sense, almost all complex numbers are transcendental. Examples * All rational numbers are algebraic. Any rational number, expressed as the quotient of an integer and a (non-zero) natural number , satisfies the above definition, because is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Numbers
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and . Though only a few classes of transcendental numbers are known—partly because it can be extremely difficult to show that a given number is transcendental—transcendental numbers are not rare. Indeed, almost all real and complex numbers are transcendental, since the algebraic numbers comprise a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic. The converse is not true: not all irrational numbers are transcendental. Hence, the set of real numbers consists of non-overlapping rational, algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dedekind Eta Function
In mathematics, the Dedekind eta function, named after Richard Dedekind, is a modular form of weight 1/2 and is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive. It also occurs in bosonic string theory. Definition For any complex number with , let ; then the eta function is defined by, :\eta(\tau) = e^\frac \prod_^\infty \left(1-e^\right) = q^\frac \prod_^\infty \left(1 - q^n\right) . Raising the eta equation to the 24th power and multiplying by gives :\Delta(\tau)=(2\pi)^\eta^(\tau) where is the modular discriminant. The presence of 24 can be understood by connection with other occurrences, such as in the 24-dimensional Leech lattice. The eta function is holomorphic on the upper half-plane but cannot be continued analytically beyond it. The eta function satisfies the functional equations :\begin \eta(\tau+1) &=e^\frac\eta(\tau),\\ \eta\left(-\frac\right) &= \sqrt\, \eta(\tau).\, \end In the second equation the bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nome (mathematics)
In mathematics, specifically the theory of elliptic functions, the nome is a special function that belongs to the non-elementary functions. This function is of great importance in the description of the elliptic functions, especially in the description of the modular identity of the Jacobi theta function, the Hermite elliptic transcendents and the Weber modular functions, that are used for solving equations of higher degrees. Definition The nome function is given by :q =\mathrm^ =\mathrm^ =\mathrm^ \, where ''K'' and iK' are the quarter periods, and \omega_1 and \omega_2 are the fundamental pair of periods, and \tau=\frac=\frac is the half-period ratio. The nome can be taken to be a function of any one of these quantities; conversely, any one of these quantities can be taken as functions of the nome. Each of them uniquely determines the others when 0 |