|
Electro-osmosis
Electroosmotic flow (or electro-osmotic flow, often abbreviated EOF; synonymous with electroosmosis or electroendosmosis) is the motion of liquid induced by an applied potential across a porous material, capillary tube, membrane, microchannel, or any other fluid conduit. Because electroosmotic velocities are independent of conduit size, as long as the electrical double layer is much smaller than the characteristic length scale of the channel, electroosmotic flow will have little effect. Electroosmotic flow is most significant when in small channels. Electroosmotic flow is an essential component in chemical separation techniques, notably capillary electrophoresis. Electroosmotic flow can occur in natural unfiltered water, as well as buffered solutions. History Electro-osmotic flow was first reported in 1807 by Ferdinand Friedrich Reuss (18 February 1778 (Tübingen, Germany) – 14 April 1852 (Stuttgart, Germany)) in an unpublished lecture before the Physical-Medical Society of Mos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeta Potential
Zeta potential is the electrical potential at the slipping plane. This plane is the interface which separates mobile fluid from fluid that remains attached to the surface. Zeta potential is a scientific term for electrokinetic potential in colloidal dispersions. In the colloidal chemistry literature, it is usually denoted using the Greek letter zeta (ζ), hence ''ζ-potential''. The usual units are volts (V) or, more commonly, millivolts (mV). From a theoretical viewpoint, the zeta potential is the electric potential in the interfacial double layer (DL) at the location of the slipping plane relative to a point in the bulk fluid away from the interface. In other words, zeta potential is the potential difference between the dispersion medium and the stationary layer of fluid attached to the dispersed particle. The zeta potential is caused by the net electrical charge contained within the region bounded by the slipping plane, and also depends on the location of that plane. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
FlowFET
A flowFET is a microfluidic component which allows the rate of flow of liquid in a microfluidic channel to be modulated by the electrical potential applied to it. In this way, it behaves as a microfluidic analogue to the field effect transistor, except that in the flowFET the flow of liquid takes the place of the flow of electric current. Indeed, the name of the flowFET is derived from the naming convention of electronic FETs (e.g. MOSFET, FINFET etc.). Mechanism of action A flowFET relies on the principle of electro-osmotic flow (EOF). In many liquid-solid interfaces, there is an electrical double layer that develops due to interactions between the two phases. In the case of a microfluidic channel, this results in a charged layer of liquid on the periphery of the fluid column which surrounds the bulk of the liquid. This electric double layer has an associated potential difference known as the zeta potential. When an appropriately-oriented electrical field is applied to this i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace’s Equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as \nabla^2\! f = 0 or \Delta f = 0, where \Delta = \nabla \cdot \nabla = \nabla^2 is the Laplace operator,The delta symbol, Δ, is also commonly used to represent a finite change in some quantity, for example, \Delta x = x_1 - x_2. Its use to represent the Laplacian should not be confused with this use. \nabla \cdot is the divergence operator (also symbolized "div"), \nabla is the gradient operator (also symbolized "grad"), and f (x, y, z) is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function. If the right-hand side is specified as a given function, h(x, y, z), we have \Delta f = h. This is called Poisson's equation, a generalization of Laplace's equation. Laplace's equation and Poisson's equation are the simpl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
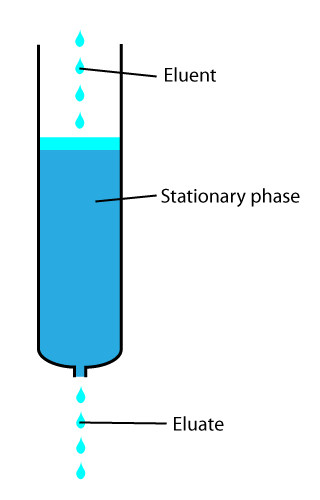
Elution Time
In analytical and organic chemistry, elution is the process of extracting one material from another by washing with a solvent; as in washing of loaded ion-exchange resins to remove captured ions. In a liquid chromatography experiment, for example, an analyte is generally adsorbed, or "bound to", an adsorbent in a liquid chromatography column. The adsorbent, a solid phase (stationary phase), is a powder which is coated onto a solid support. Based on an adsorbent's composition, it can have varying affinities to "hold" onto other molecules—forming a thin film on the surface of its particles. Elution then is the process of removing analytes from the adsorbent by running a solvent, called an "eluent", past the adsorbent/analyte complex. As the solvent molecules "elute", or travel down through the chromatography column, they can either pass by the adsorbent/analyte complex or they can displace the analyte by binding to the adsorbent in its place. After the solvent molecules displa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oxide
An oxide () is a chemical compound that contains at least one oxygen atom and one other element in its chemical formula. "Oxide" itself is the dianion of oxygen, an O2– (molecular) ion. with oxygen in the oxidation state of −2. Most of the Earth's crust consists of oxides. Even materials considered pure elements often develop an oxide coating. For example, aluminium foil develops a thin skin of Al2O3 (called a passivation layer) that protects the foil from further corrosion.Greenwood, N. N.; & Earnshaw, A. (1997). Chemistry of the Elements (2nd Edn.), Oxford:Butterworth-Heinemann. . Stoichiometry (the measurable relationship between reactants and chemical equations of a equation or reaction) Oxides are extraordinarily diverse in terms of stoichiometries and in terms of the structures of each stoichiometry. Most elements form oxides of more than one stoichiometry. A well known example is carbon monoxide and carbon dioxide.Greenwood, N. N.; & Earnshaw, A. (1997). Chemistry ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microfluidic
Microfluidics refers to the behavior, precise control, and manipulation of fluids that are geometrically constrained to a small scale (typically sub-millimeter) at which surface forces dominate volumetric forces. It is a multidisciplinary field that involves engineering, physics, chemistry, biochemistry, nanotechnology, and biotechnology. It has practical applications in the design of systems that process low volumes of fluids to achieve multiplexing, automation, and high-throughput screening. Microfluidics emerged in the beginning of the 1980s and is used in the development of inkjet printheads, DNA chips, lab-on-a-chip technology, micro-propulsion, and micro-thermal technologies. Typically, micro means one of the following features: * Small volumes (μL, nL, pL, fL) * Small size * Low energy consumption * Microdomain effects Typically microfluidic systems transport, mix, separate, or otherwise process fluids. Various applications rely on passive fluid control using capillary for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Temperature
Thermodynamic temperature is a quantity defined in thermodynamics as distinct from kinetic theory or statistical mechanics. Historically, thermodynamic temperature was defined by Kelvin in terms of a macroscopic relation between thermodynamic work and heat transfer as defined in thermodynamics, but the kelvin was redefined by international agreement in 2019 in terms of phenomena that are now understood as manifestations of the kinetic energy of free motion of microscopic particles such as atoms, molecules, and electrons. From the thermodynamic viewpoint, for historical reasons, because of how it is defined and measured, this microscopic kinetic definition is regarded as an "empirical" temperature. It was adopted because in practice it can generally be measured more precisely than can Kelvin's thermodynamic temperature. A thermodynamic temperature reading of zero is of particular importance for the third law of thermodynamics. By convention, it is reported on the ''Kelvin scale'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, and in Planck's law of black-body radiation and Boltzmann's entropy formula, and is used in calculating thermal noise in resistors. The Boltzmann constant has dimensions of energy divided by temperature, the same as entropy. It is named after the Austrian scientist Ludwig Boltzmann. As part of the 2019 redefinition of SI base units, the Boltzmann constant is one of the seven " defining constants" that have been given exact definitions. They are used in various combinations to define the seven SI base units. The Boltzmann constant is defined to be exactly . Roles of the Boltzmann constant Macroscopically, the ideal gas law states that, for an ideal gas, the product of pressure and volume is proportional to the product of amount of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Charge
The elementary charge, usually denoted by is the electric charge carried by a single proton or, equivalently, the magnitude of the negative electric charge carried by a single electron, which has charge −1 . This elementary charge is a fundamental physical constant. In the SI system of units, the value of the elementary charge is exactly defined as e = coulombs, or 160.2176634 zeptocoulombs (zC). Since the 2019 redefinition of SI base units, the seven SI base units are defined by seven fundamental physical constants, of which the elementary charge is one. In the centimetre–gram–second system of units (CGS), the corresponding quantity is . Robert A. Millikan and Harvey Fletcher's oil drop experiment first directly measured the magnitude of the elementary charge in 1909, differing from the modern accepted value by just 0.6%. Under assumptions of the then-disputed atomic theory, the elementary charge had also been indirectly inferred to ~3% accuracy from bla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Diffusivity
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of 16 mm2/s, and in water its diffusion coefficient is 0.0016 mm2/s. Diffusivity has dimensions of length2 / time, or m2/s in SI units and cm2/s in CGS units. Temperature dependence of the diffusion coefficient Solids The diffusion coefficient in solids at different temperatures is generally found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Vector Potential
In classical electromagnetism, magnetic vector potential (often called A) is the vector quantity defined so that its curl is equal to the magnetic field: \nabla \times \mathbf = \mathbf. Together with the electric potential ''φ'', the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials ''φ'' and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields. Magnetic vector potential was first introduced by Franz Ernst Neumann and Wilhelm Eduard Weber in 1845 and in 1846, respectively. Lord Kelvin also introduced vector potential in 1847, along with the formula relating it to the magnetic field. Magnetic vector potential The magnetic vector potential A is a vector field, defined along with the electric potential ''ϕ'' (a scalar field) by the equations: \mathbf = \n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nernst–Planck Equation
The Nernst–Planck equation is a conservation of mass equation used to describe the motion of a charged chemical species in a fluid medium. It extends Fick's law of diffusion for the case where the diffusing particles are also moved with respect to the fluid by electrostatic forces. It is named after Walther Nernst and Max Planck. Equation The Nernst–Planck equation is a continuity equation for the time-dependent concentration c(t,) of a chemical species: : + \nabla \cdot = 0 where is the flux. It is assumed that the total flux is composed of three elements: diffusion, advection, and electromigration. This implies that the concentration is affected by an ionic concentration gradient \nabla c, flow velocity , and an electric field : : = -\underbrace_ + \underbrace_ +\underbrace_ where D is the diffusivity of the chemical species, z is the valence of ionic species, e is the elementary charge, k_\text is the Boltzmann constant, and T is the absolute temperature. The ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |