|
Einstein–Rosen Bridge
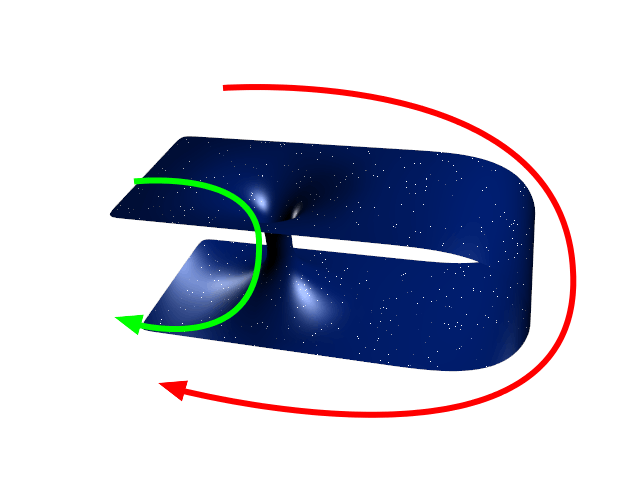
A wormhole (Einstein-Rosen bridge) is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations. A wormhole can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen. Many scientists postulate that wormholes are merely projections of a fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. Theoretically, a wormhole might connect extremely long distances such as a billion light years, or short distances such as a few meters, or different points in time, or even different universes. In 1995, Matt Visser suggested there may be many wormholes in the universe if cosmic strings with negative mass were generated in the early un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein-Rosen Bridge
A wormhole ( Einstein-Rosen bridge) is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations. A wormhole can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen. Many scientists postulate that wormholes are merely projections of a fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. Theoretically, a wormhole might connect extremely long distances such as a billion light years, or short distances such as a few meters, or different points in time, or even different universes. In 1995, Matt Visser suggested there may be many wormholes in the universe if cosmic strings with negative mass were generated in the early ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2D Plane
In mathematics, a plane is a Euclidean (flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an axiomatic t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry And Topology
In mathematics, geometry and topology is an umbrella term for the historically distinct disciplines of geometry and topology, as general frameworks allow both disciplines to be manipulated uniformly, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory. Sharp distinctions between geometry and topology can be drawn, however, as discussed below. It is also the title of a journal '' Geometry & Topology'' that covers these topics. Scope It is distinct from "geometric topology", which more narrowly involves applications of topology to geometry. It includes: * Differential geometry and topology * Geometric topology (including low-dimensional topology and surgery theory) It does not include such parts of algebraic topology as homotopy theory, but some areas of geometry and topology (such as surgery theory, particularly algebraic surgery theory) are heavily algebraic. Distinction between geometry a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Physics
''Annals of Physics'' is a monthly peer-reviewed scientific journal covering all aspects of physics. It was established in 1957 and is published by Elsevier. The editor-in-chief is Neil Turok ( University of Edinburgh School of Physics and Astronomy). Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 2.73. References External links * Physics journals Monthly journals Publications established in 1957 English-language journals Elsevier academic journals {{physics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Handle Decomposition
In mathematics, a handle decomposition of an ''m''-manifold ''M'' is a union \emptyset = M_ \subset M_0 \subset M_1 \subset M_2 \subset \dots \subset M_ \subset M_m = M where each M_i is obtained from M_ by the attaching of i-handles. A handle decomposition is to a manifold what a CW complex, CW-decomposition is to a topological space—in many regards the purpose of a handle decomposition is to have a language analogous to CW-complexes, but adapted to the world of smooth manifolds. Thus an ''i''-handle is the smooth analogue of an ''i''-cell. Handle decompositions of manifolds arise naturally via Morse theory. The modification of handle structures is closely linked to Cerf theory. Motivation Consider the standard CW-complex, CW-decomposition of the ''n''-sphere, with one zero cell and a single ''n''-cell. From the point of view of smooth manifolds, this is a degenerate decomposition of the sphere, as there is no natural way to see the smooth structure of S^n from the eyes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topologist
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
