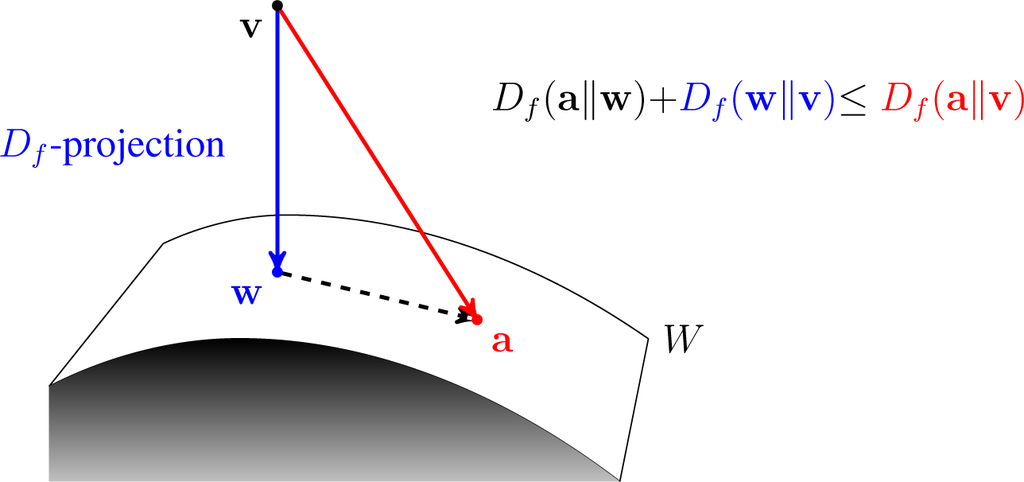
|
Expectation Propagation
Expectation propagation (EP) is a technique in Bayesian machine learning. EP finds approximations to a probability distribution. It uses an iterative approach that uses the factorization structure of the target distribution. It differs from other Bayesian approximation approaches such as variational Bayesian methods. More specifically, suppose we wish to approximate an intractable probability distribution p(\mathbf) with a tractable distribution q(\mathbf). Expectation propagation achieves this approximation by minimizing the Kullback-Leibler divergence \mathrm(p, , q). Variational Bayesian methods minimize \mathrm(q, , p) instead. If q(\mathbf) is a Gaussian \mathcal(\mathbf, \mu, \Sigma), then \mathrm(p, , q) is minimized with \mu and \Sigma being equal to the mean of p(\mathbf) and the covariance of p(\mathbf), respectively; this is called moment matching. Applications Expectation propagation via moment matching plays a vital role in approximation for indicator functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes the posterior probability according to Bayes' theorem: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iterative
Iteration is the repetition of a process in order to generate a (possibly unbounded) sequence of outcomes. Each repetition of the process is a single iteration, and the outcome of each iteration is then the starting point of the next iteration. In mathematics and computer science, iteration (along with the related technique of recursion) is a standard element of algorithms. Mathematics In mathematics, iteration may refer to the process of iterating a function, i.e. applying a function repeatedly, using the output from one iteration as the input to the next. Iteration of apparently simple functions can produce complex behaviors and difficult problems – for examples, see the Collatz conjecture and juggler sequences. Another use of iteration in mathematics is in iterative methods which are used to produce approximate numerical solutions to certain mathematical problems. Newton's method is an example of an iterative method. Manual calculation of a number's square root is a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Bayesian Methods
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the ''sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the ''population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of mean are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Matching
Moment or Moments may refer to: * Present time Music * The Moments, American R&B vocal group Albums * ''Moment'' (Dark Tranquillity album), 2020 * ''Moment'' (Speed album), 1998 * ''Moments'' (Darude album) * ''Moments'' (Christine Guldbrandsen album) * ''Moments'' (Mark Holden album), 1995 * ''Moments'' (Leo Ku album) * ''Moments'' (Barbara Mandrell album) * ''Moments'' (Andrew Rayel album) * ''Moments'' (Boz Scaggs album) Songs * "Moment" (Blanche song) (2018) * "Moment" (SMAP song) (2012) * "Moment", a song by Aiden from ''Conviction'' * "Moment", a 2014 song by Young Money from '' Young Money: Rise of an Empire'', featuring Lil Wayne * "Moments" (Hans Bollandsås song) (2010) * "Moments" (Emerson Drive song) (2007) * "Moments" (Ayumi Hamasaki song) (2004) * "Moments" (Tove Lo song) (2014) * "Moments" (One Direction song) (2011) * "Moments" (Freddy Verano song) * "Moments", a song by Westlife from ''Westlife'' Film and television * ''Moment'' (film), a 1978 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indicator Functions
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , one has \mathbf_(x)=1 if x\in A, and \mathbf_(x)=0 otherwise, where \mathbf_A is a common notation for the indicator function. Other common notations are I_A, and \chi_A. The indicator function of is the Iverson bracket of the property of belonging to ; that is, :\mathbf_(x)= \in A For example, the Dirichlet function is the indicator function of the rational numbers as a subset of the real numbers. Definition The indicator function of a subset of a set is a function \mathbf_A \colon X \to \ defined as \mathbf_A(x) := \begin 1 ~&\text~ x \in A~, \\ 0 ~&\text~ x \notin A~. \end The Iverson bracket provides the equivalent notation, \in A/math> or to be used instead of \mathbf_(x)\,. The function \mathbf_A is sometimes denoted , , , or even just . Notatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belief Propagation
A belief is an attitude that something is the case, or that some proposition is true. In epistemology, philosophers use the term "belief" to refer to attitudes about the world which can be either true or false. To believe something is to take it to be true; for instance, to believe that snow is white is comparable to accepting the truth of the proposition "snow is white". However, holding a belief does not require active introspection. For example, few carefully consider whether or not the sun will rise tomorrow, simply assuming that it will. Moreover, beliefs need not be ''occurrent'' (e.g. a person actively thinking "snow is white"), but can instead be ''dispositional'' (e.g. a person who if asked about the color of snow would assert "snow is white"). There are various different ways that contemporary philosophers have tried to describe beliefs, including as representations of ways that the world could be (Jerry Fodor), as dispositions to act as if certain things are true (Rod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
TrueSkill
TrueSkill is a skill-based ranking system developed by Microsoft for use with video game matchmaking on Xbox Live. Unlike the popular Elo rating system, which was initially designed for chess, TrueSkill is designed to support games with more than two players. In 2018, Microsoft published details about an extended version of TrueSkill, named TrueSkill2. Calculation A player's skill is represented as a normal distribution \mathcal characterized by a mean value of \mu (mu, representing perceived skill) and a variance of \sigma (sigma, representing how "unconfident" the system is in the player's \mu value). As such \mathcal(x) can be interpreted as the probability that the player's "true" skill is x. On Xbox Live, players start with \mu = 25 and \sigma = 25/3; \mu always increases after a win and always decreases after a loss. The extent of actual updates depends on each player's \sigma and on how "surprising" the outcome is to the system. Unbalanced games, for example, result in eith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making predicti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Probability Distribution")
