|
Euler Number (physics)
The Euler number (Eu) is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop caused by a restriction and the kinetic energy per volume of the flow, and is used to characterize energy losses in the flow, where a perfect frictionless flow corresponds to an Euler number of 0. The inverse of the Euler number is referred to as the Ruark Number with the symbol Ru. The Euler number is defined as \mathrm = \frac = \frac = \frac = \frac where *\rho is the density of the fluid. *p_u is the upstream pressure. *p_d is the downstream pressure. *v is a characteristic velocity of the flow. An alternative definition of the Euler number is given by Shah and SekulicShah and Sekulic, Fundamentals of Heat Exchanger Design, John Wiley & Sons, Inc. 2003 \mathrm = \frac = \frac where * \Delta p is the pressure drop = p_u - p_d See also * Darcy–Weisbach equation is a different way of interpr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Number
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into unit of measurement, units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined Unit of measurement, units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific Unit of volume, units of volume used, such as in milliliters per milliliter (mL/mL). The 1, number one is recognized as a dimensionless Base unit of measurement, base quantity. Radians serve as dimensionless units for Angle, angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Flow
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various #Units, units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the International System of Units, SI unit of pressure, the Pascal (unit), pascal (Pa), for example, is one newton (unit), newton per square metre (N/m2); similarly, the Pound (force), pound-force per square inch (Pound per square inch, psi, symbol lbf/in2) is the traditional unit of pressure in the imperial units, imperial and United States customary units, US customary systems. Pressure ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinetic Energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion. In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Robert and Halliday, David (1960) ''Physics'', Section 7-5, Wiley International Edition The kinetic energy of an object is equal to the work, or force ( F) in the direction of motion times its displacement ( s), needed to accelerate the object from rest to its given speed. The same amount of work is done by the object when decelerating from its current speed to a state of rest. The SI unit of energy is the joule, while the English unit of energy is the foot-pound. In relativistic mechanics, \fracmv^2 is a good approximation of kinetic energy only when ''v'' is much less than the speed of light. History and etymology The adjective ''kinetic'' has its roots in the Greek word κίνησις ''kinesis'', meaning "motion". The dichoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darcy–Weisbach Equation
In fluid dynamics, the Darcy–Weisbach equation is an Empirical research, empirical equation that relates the head loss, or pressure loss, due to friction along a given length of pipe to the average velocity of the fluid flow for an incompressible fluid. The equation is named after Henry Darcy and Julius Weisbach. Currently, there is no formula more accurate or universally applicable than the Darcy-Weisbach supplemented by the Moody diagram or Colebrook equation. The Darcy–Weisbach equation contains a dimension analysis, dimensionless friction factor, known as the Darcy friction factor. This is also variously called the Darcy–Weisbach friction factor, friction factor, resistance coefficient, or flow coefficient. Historical background The Darcy-Weisbach equation, combined with the Moody chart for calculating head losses in pipes, is traditionally attributed to Henry Darcy, Julius Weisbach, and Lewis Ferry Moody. However, the development of these formulas and charts also involv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reynolds Number
In fluid dynamics, the Reynolds number () is a dimensionless quantity that helps predict fluid flow patterns in different situations by measuring the ratio between Inertia, inertial and viscous forces. At low Reynolds numbers, flows tend to be dominated by laminar flow, laminar (sheet-like) flow, while at high Reynolds numbers, flows tend to be turbulence, turbulent. The turbulence results from differences in the fluid's speed and direction, which may sometimes intersect or even move counter to the overall direction of the flow (Eddy (fluid dynamics), eddy currents). These eddy currents begin to churn the flow, using up energy in the process, which for liquids increases the chances of cavitation. The Reynolds number has wide applications, ranging from liquid flow in a pipe to the passage of air over an aircraft wing. It is used to predict the transition from laminar–turbulent transition, laminar to turbulent flow and is used in the scaling of similar but different-sized fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
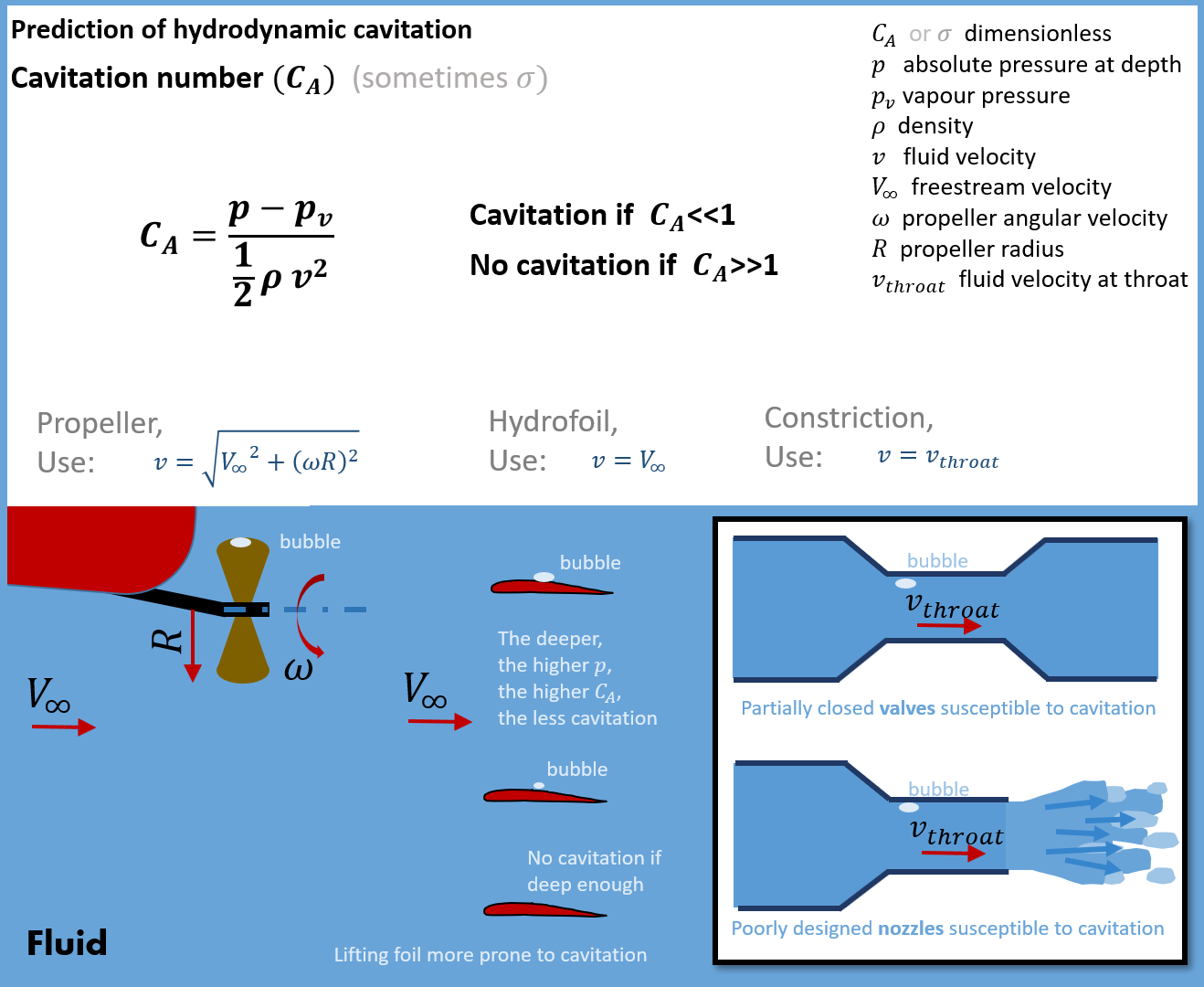
Cavitation Number
There are three dimensionless numbers that may be referred to as the cavitation number in various scenarios: the cavitation number for hydrodynamic cavitation, the Thoma number for cavitation in pumps, and the Garcia-Atance number for ultrasonic cavitation (named after Gonzalo Garcia-Atance Fatjo). Hydrodynamic cavitation The cavitation number (Ca) can be used to predict hydrodynamic cavitation. It has a similar structure as the Euler number, but a different meaning and use: The cavitation number expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume, and is used to characterize the potential of the flow to cavitate. It is defined as \mathrm = \frac where *\rho is the density of the fluid. *p is the local pressure. *p_\mathrm is the vapor pressure of the fluid. *v is a characteristic velocity of the flow. The cavitation number serves as one of the primary methods for characterizing cavitation w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Numbers Of Fluid Mechanics
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into unit of measurement, units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that align with another system, these quantities do not necessitate explicitly defined Unit of measurement, units. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific Unit of volume, units of volume used, such as in milliliters per milliliter (mL/mL). The 1, number one is recognized as a dimensionless Base unit of measurement, base quantity. Radians serve as dimensionless units for Angle, angular measurements, derived from the universal ratio of 2π times the radius of a circle being equal to its circumference. Dimensionless quantities play a crucial role serving as parameters in differential equations in various technical disciplines. In calculus, concepts like the unitless ratios ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |