|
Equivalent Rectangular Bandwidth
The equivalent rectangular bandwidth or ERB is a measure used in psychoacoustics, which gives an approximation to the bandwidths of the filters in human hearing, using the unrealistic but convenient simplification of modeling the filters as rectangular band-pass filters, or band-stop filters, like in tailor-made notched music training (TMNMT). Approximations For moderate sound levels and young listeners, the bandwidth of human auditory filters can be approximated by the polynomial equation: where ''f'' is the center frequency of the filter in kHz and ERB(''f'') is the bandwidth of the filter in Hz. The approximation is based on the results of a number of published simultaneous masking experiments and is valid from 0.1 to 6.5 kHz.B.C.J. Moore and B.R. Glasberg, "Suggested formulae for calculating auditory-filter bandwidths and excitation patterns" Journal of the Acoustical Society of America 74: 750-753, 1983. The above approximation was given in 1983 by Moore and Glasber ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Psychoacoustics
Psychoacoustics is the branch of psychophysics involving the scientific study of sound perception and audiology—how humans perceive various sounds. More specifically, it is the branch of science studying the psychological responses associated with sound (including noise, speech, and music). Psychoacoustics is an interdisciplinary field of many areas, including psychology, acoustics, electronic engineering, physics, biology, physiology, and computer science. Background Hearing is not a purely mechanical phenomenon of wave propagation, but is also a sensory and perceptual event; in other words, when a person hears something, that something arrives at the ear as a mechanical sound wave traveling through the air, but within the ear it is transformed into neural action potentials. The outer hair cells (OHC) of a mammalian cochlea give rise to enhanced sensitivity and better frequency resolution of the mechanical response of the cochlear partition. These nerve pulses then travel to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
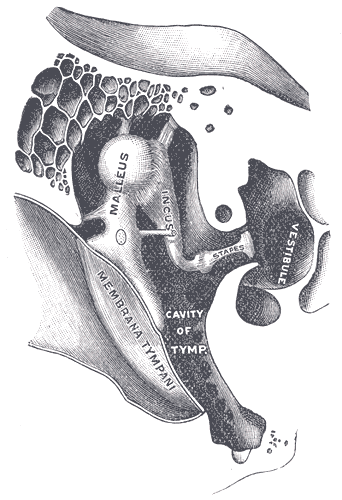
Human Hearing
Hearing, or auditory perception, is the ability to perceive sounds through an organ, such as an ear, by detecting vibrations as periodic changes in the pressure of a surrounding medium. The academic field concerned with hearing is auditory science. Sound may be heard through solid, liquid, or gaseous matter. It is one of the traditional five senses. Partial or total inability to hear is called hearing loss. In humans and other vertebrates, hearing is performed primarily by the auditory system: mechanical waves, known as vibrations, are detected by the ear and transduced into nerve impulses that are perceived by the brain (primarily in the temporal lobe). Like touch, audition requires sensitivity to the movement of molecules in the world outside the organism. Both hearing and touch are types of mechanosensation. Hearing mechanism There are three main components of the human auditory system: the outer ear, the middle ear, and the inner ear. Outer ear The outer ear inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Band-pass Filter
A band-pass filter or bandpass filter (BPF) is a device that passes frequencies within a certain range and rejects (attenuates) frequencies outside that range. Description In electronics and signal processing, a filter is usually a two-port circuit or device which removes frequency components of a signal (an alternating voltage or current). A band-pass filter allows through components in a specified band of frequencies, called its ''passband'' but blocks components with frequencies above or below this band. This contrasts with a high-pass filter, which allows through components with frequencies above a specific frequency, and a low-pass filter, which allows through components with frequencies below a specific frequency. In digital signal processing, in which signals represented by digital numbers are processed by computer programs, a band-pass filter is a computer algorithm that performs the same function. The term band-pass filter is also used for optical filters, sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simultaneous Masking
In audio signal processing, auditory masking occurs when the perception of one sound is affected by the presence of another sound.Gelfand, S.A. (2004) ''Hearing – An Introduction to Psychological and Physiological Acoustics'' 4th Ed. New York, Marcel Dekker Auditory masking in the frequency domain is known as simultaneous masking, frequency masking or spectral masking. Auditory masking in the time domain is known as temporal masking or non-simultaneous masking. Masked threshold The ''unmasked threshold'' is the quietest level of the signal which can be perceived without a masking signal present. The ''masked threshold'' is the quietest level of the signal perceived when combined with a specific masking noise. The amount of masking is the difference between the masked and unmasked thresholds. Gelfand provides a basic example.Gelfand, S.A. (2004) ''Hearing – An Introduction to Psychological and Physiological Acoustics'' 4th Ed. New York, Marcel Dekker Let us say that for a g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology. Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly. Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Of Integration
In calculus, the constant of integration, often denoted by C (or c), is a constant term added to an antiderivative of a function f(x) to indicate that the indefinite integral of f(x) (i.e., the set of all antiderivatives of f(x)), on a connected domain, is only defined up to an additive constant. This constant expresses an ambiguity inherent in the construction of antiderivatives. More specifically, if a function f(x) is defined on an interval, and F(x) is an antiderivative of f(x), then the set of ''all'' antiderivatives of f(x) is given by the functions F(x) + C, where C is an arbitrary constant (meaning that ''any'' value of C would make F(x) + C a valid antiderivative). For that reason, the indefinite integral is often written as \int f(x) \, dx = F(x) + C, although the constant of integration might be sometimes omitted in lists of integrals for simplicity. Origin The derivative of any constant function is zero. Once one has found one antiderivative F(x) for a function f(x) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. As of 2020, MATLAB has more than 4 million users worldwide. They come from various backgrounds of engineering, science, and economics. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was based on his 1960s PhD thesis. Moler became a math professor at the University of New Mexico and starte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ . For a function f\colon X\to Y, its inverse f^\colon Y\to X admits an explicit description: it sends each element y\in Y to the unique element x\in X such that . As an example, consider the real-valued function of a real variable given by . One can think of as the function which multiplies its input by 5 then subtracts 7 from the result. To undo this, one adds 7 to the input, then divides the result by 5. Therefore, the inverse of is the function f^\colon \R\to\R defined by f^(y) = \frac . Definitions Let be a function whose domain is the set , and whose codomain is the set . Then is ''invertible'' if there exists a function from to such that g(f(x))=x for all x\in X and f(g(y))=y for all y\in Y. If is invertible, then there is exactly one function sat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Critical Bands
In audiology and psychoacoustics the concept of critical bands, introduced by Harvey Fletcher in 1933 and refined in 1940, describes the frequency bandwidth of the "auditory filter" created by the cochlea, the sense organ of hearing within the inner ear. Roughly, the critical band is the band of audio frequencies within which a second tone will interfere with the perception of the first tone by auditory masking. Psychophysiologically, beating and auditory roughness sensations can be linked to the inability of the auditory frequency-analysis mechanism to resolve inputs whose frequency difference is smaller than the critical bandwidth and to the resulting irregular "tickling" of the mechanical system (basilar membrane) that resonates in response to such inputs. Critical bands are also closely related to auditory masking phenomena – reduced audibility of a sound signal when in the presence of a second signal of higher intensity within the same critical band. Masking phenomena have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
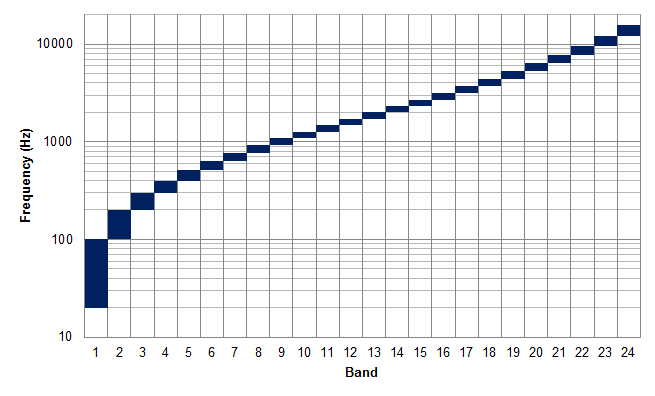
Bark Scale
The Bark scale is a psychoacoustical scale proposed by Eberhard Zwicker in 1961. It is named after Heinrich Barkhausen who proposed the first subjective measurements of loudness.Zwicker, E. (1961),Subdivision of the audible frequency range into critical bands" ''The Journal of the Acoustical Society of America'', Volume 33, Issue 2, p. 248 (1961) One definition of the term is "...a frequency scale on which equal distances correspond with perceptually equal distances. Above about 500 Hz this scale is more or less equal to a logarithmic frequency axis. Below 500 Hz the Bark scale becomes more and more linear." The scale ranges from 1 to 24 and corresponds to the first 24 critical bands of hearing. It is related to, but somewhat less popular than, the mel scale, a perceptual scale of pitches judged by listeners to be equal in distance from one another. Bark scale critical bands Since the direct measurements of the critical bands are subject to error, the values in this tab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
