|
Equidistant Conic With Tissot's Indicatrices Of Distortion
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal. In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in ''n''-space is an (''n''−1)-space. For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other tangential polygon is equidistant from the points of tangency of the polygon's sides with the circle. Every point on a perpendicular bisector of the side of a triangle or other polygon is equidist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular Bisector
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes through the midpoint of a given segment) and the ''angle bisector'' (a line that passes through the apex of an angle, that divides it into two equal angles). In three-dimensional space, bisection is usually done by a plane, also called the ''bisector'' or ''bisecting plane''. Perpendicular line segment bisector Definition *The perpendicular bisector of a line segment is a line, which meets the segment at its midpoint perpendicularly. The Horizontal intersector of a segment AB also has the property that each of its points X is equidistant from the segment's endpoints: (D)\quad , XA, = , XB, . The proof follows from and Pythagoras' theorem: :, XA, ^2=, XM, ^2+, MA, ^2=, XM, ^2+, MB, ^2=, XB, ^2 \; . Property (D) is usually used for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombi, with two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercycle (hyperbolic Geometry)
In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line (its axis). Given a straight line and a point not on , one can construct a hypercycle by taking all points on the same side of as , with perpendicular distance to equal to that of . The line is called the ''axis'', ''center'', or ''base line'' of the hypercycle. The lines perpendicular to , which are also perpendicular to the hypercycle, are called the ''normals'' of the hypercycle. The segments of the normals between and the hypercycle are called the ''radii''. Their common length is called the ''distance'' or ''radius'' of the hypercycle. The hypercycles through a given point that share a tangent through that point converge towards a horocycle as their distances go towards infinity. Properties similar to those of Euclidean lines Hypercycles in hyperbolic geometry have some properties similar to those of lines in Eu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P'' not on ''R'', in the plane containing both line ''R'' and point ''P'' there are at least two distinct lines through ''P'' that do not intersect ''R''. (Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.) Hyperbolic plane geometry is also the geometry of pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they locally resemble the hyperbolic plane. A modern use of hyperbolic geometry is in the theory of special relativity, particularly the Minkowski model. When geometers first realised they were working with something other than the standard Euclidean geometry, they described their geomet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Lines
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have analogous properties that are referred to as parallelism. Symbol The parallel symbol is \parallel. For example, AB \parallel CD indicates that line ''AB'' is parallel to line ''CD''. In the Unicode character set, the "parallel" and "not parallel" signs have codepoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary (topology)
In topology and mathematics in general, the boundary of a subset of a topological space is the set of points in the closure of not belonging to the interior of . An element of the boundary of is called a boundary point of . The term boundary operation refers to finding or taking the boundary of a set. Notations used for boundary of a set include \operatorname(S), \operatorname(S), and \partial S. Some authors (for example Willard, in ''General Topology'') use the term frontier instead of boundary in an attempt to avoid confusion with a different definition used in algebraic topology and the theory of manifolds. Despite widespread acceptance of the meaning of the terms boundary and frontier, they have sometimes been used to refer to other sets. For example, ''Metric Spaces'' by E. T. Copson uses the term boundary to refer to Hausdorff's border, which is defined as the intersection of a set with its boundary. Hausdorff also introduced the term residue, which is defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape
A shape or figure is a graphics, graphical representation of an object or its external boundary, outline, or external Surface (mathematics), surface, as opposed to other properties such as color, Surface texture, texture, or material type. A plane shape or plane figure is constrained to lie on a ''plane (geometry), plane'', in contrast to ''solid figure, solid'' 3D shapes. A two-dimensional shape or two-dimensional figure (also: 2D shape or 2D figure) may lie on a more general curved ''surface (mathematics), surface'' (a non-Euclidean two-dimensional space). Classification of simple shapes Some simple shapes can be put into broad categories. For instance, polygons are classified according to their number of edges as triangles, quadrilaterals, pentagons, etc. Each of these is divided into smaller categories; triangles can be equilateral, isosceles, obtuse triangle, obtuse, Triangle#By internal angles, acute, Triangle, scalene, etc. while quadrilaterals can be rectangles, rho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Medial Axis
The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced in 1967 by Harry Blum as a tool for biological shape recognition. In mathematics the closure of the medial axis is known as the cut locus. In 2D, the medial axis of a subset ''S'' which is bounded by planar curve ''C'' is the locus of the centers of circles that are tangent to curve ''C'' in two or more points, where all such circles are contained in ''S''. (It follows that the medial axis itself is contained in ''S''.) The medial axis of a simple polygon is a tree whose leaves are the vertices of the polygon, and whose edges are either straight segments or arcs of parabolas. The medial axis together with the associated radius function of the maximally inscribed discs is called the medial axis transform (MAT). The medial axis transform is a complete shape descriptor (see also shape analysis), ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Skeleton
In shape analysis, skeleton (or topological skeleton) of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width. Together with the distance of its points to the shape boundary, the skeleton can also serve as a representation of the shape (they contain all the information necessary to reconstruct the shape). Skeletons have several different mathematical definitions in the technical literature, and there are many different algorithms for computing them. Various different variants of skeleton can also be found, including straight skeletons, morphological skeletons, etc. In the technical literature, the concepts of skeleton and medial axis are used interchangeably by some authors,, Section 11.1.5, p. 650 while some other authors, Section 9.9, p. 382., Section 17.5.2, p. 234. regard them as relate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shape Analysis (digital Geometry)
This article describes shape analysis to analyze and process geometric shapes. Description ''Shape analysis'' is the (mostly) automatic analysis of geometric shapes, for example using a computer to detect similarly shaped objects in a database or parts that fit together. For a computer to automatically analyze and process geometric shapes, the objects have to be represented in a digital form. Most commonly a boundary representation is used to describe the object with its boundary (usually the outer shell, see also 3D model). However, other volume based representations (e.g. constructive solid geometry) or point based representations (point clouds) can be used to represent shape. Once the objects are given, either by modeling (computer-aided design), by scanning (3D scanner) or by extracting shape from 2D or 3D images, they have to be simplified before a comparison can be achieved. The simplified representation is often called a ''shape descriptor'' (or fingerprint, signature). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Focus (geometry)
In geometry, focuses or foci (), singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an ''n''-ellipse. Conic sections Defining conics in terms of two foci An ellipse can be defined as the locus of points for which the sum of the distances to two given foci is constant. A circle is the special case of an ellipse in which the two foci coincide with each other. Thus, a circle can be more simply defined as the locus of points each of which is a fixed distance from a single given focus. A circle can also be defined as the circle of Apollonius, in terms of two different foci, as the locus of points having a fixed ratio of distances to the two foci. A parabola is a li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point where the parabola intersects its axis of symmetry is called the "vertex" and is the point where the parabola is most sharply curved. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
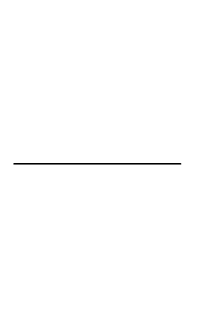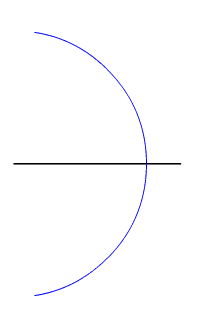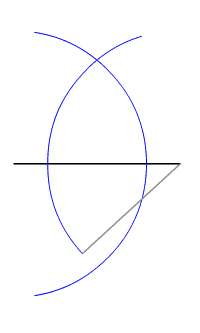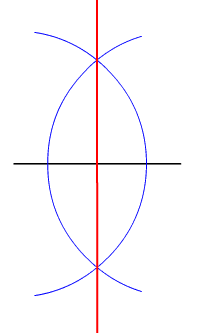
.png)
