|
Einstein–Rosen Bridge
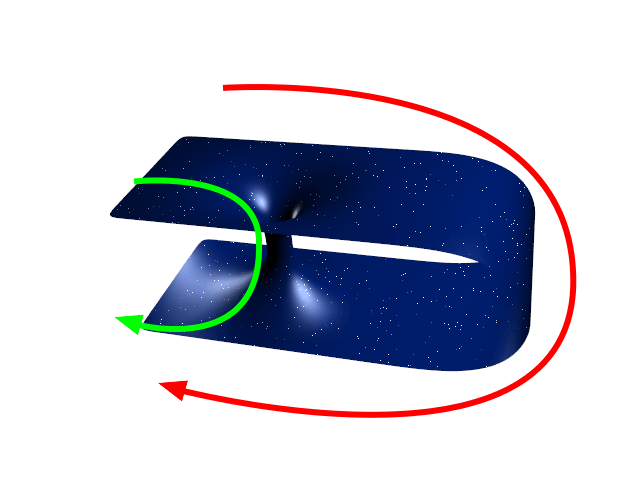
A wormhole (Einstein-Rosen bridge) is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations. A wormhole can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen. Many scientists postulate that wormholes are merely projections of a fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. Theoretically, a wormhole might connect extremely long distances such as a billion light years, or short distances such as a few meters, or different points in time, or even different universes. In 1995, Matt Visser suggested there may be many wormholes in the universe if cosmic strings with negative mass were generated in the early un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Einstein-Rosen Bridge
A wormhole ( Einstein-Rosen bridge) is a hypothetical structure connecting disparate points in spacetime, and is based on a special solution of the Einstein field equations. A wormhole can be visualized as a tunnel with two ends at separate points in spacetime (i.e., different locations, different points in time, or both). Wormholes are consistent with the general theory of relativity, but whether wormholes actually exist remains to be seen. Many scientists postulate that wormholes are merely projections of a fourth spatial dimension, analogous to how a two-dimensional (2D) being could experience only part of a three-dimensional (3D) object. Theoretically, a wormhole might connect extremely long distances such as a billion light years, or short distances such as a few meters, or different points in time, or even different universes. In 1995, Matt Visser suggested there may be many wormholes in the universe if cosmic strings with negative mass were generated in the early ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2D Plane
In mathematics, a plane is a Euclidean (flat), two-dimensional surface that extends indefinitely. A plane is the two-dimensional analogue of a point (zero dimensions), a line (one dimension) and three-dimensional space. Planes can arise as subspaces of some higher-dimensional space, as with one of a room's walls, infinitely extended, or they may enjoy an independent existence in their own right, as in the setting of two-dimensional Euclidean geometry. Sometimes the word ''plane'' is used more generally to describe a two-dimensional surface, for example the hyperbolic plane and elliptic plane. When working exclusively in two-dimensional Euclidean space, the definite article is used, so ''the'' plane refers to the whole space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional space, often in the plane. Euclidean geometry Euclid set forth the first great landmark of mathematical thought, an axiomatic t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry And Topology
In mathematics, geometry and topology is an umbrella term for the historically distinct disciplines of geometry and topology, as general frameworks allow both disciplines to be manipulated uniformly, most visibly in local to global theorems in Riemannian geometry, and results like the Gauss–Bonnet theorem and Chern–Weil theory. Sharp distinctions between geometry and topology can be drawn, however, as discussed below. It is also the title of a journal ''Geometry & Topology'' that covers these topics. Scope It is distinct from "geometric topology", which more narrowly involves applications of topology to geometry. It includes: * Differential geometry and topology * Geometric topology (including low-dimensional topology and surgery theory) It does not include such parts of algebraic topology as homotopy theory, but some areas of geometry and topology (such as surgery theory, particularly algebraic surgery theory) are heavily algebraic. Distinction between geometry and top ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Physics
''Annals of Physics'' is a monthly peer-reviewed scientific journal covering all aspects of physics. It was established in 1957 and is published by Elsevier. The editor-in-chief is Neil Turok (University of Edinburgh School of Physics and Astronomy). Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2020 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 2.73. References External links * Physics journals Monthly journals Publications established in 1957 English-language journals Elsevier academic journals {{physics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Handle Decomposition
In mathematics, a handle decomposition of an ''m''-manifold ''M'' is a union \emptyset = M_ \subset M_0 \subset M_1 \subset M_2 \subset \dots \subset M_ \subset M_m = M where each M_i is obtained from M_ by the attaching of i-handles. A handle decomposition is to a manifold what a CW complex, CW-decomposition is to a topological space—in many regards the purpose of a handle decomposition is to have a language analogous to CW-complexes, but adapted to the world of smooth manifolds. Thus an ''i''-handle is the smooth analogue of an ''i''-cell. Handle decompositions of manifolds arise naturally via Morse theory. The modification of handle structures is closely linked to Cerf theory. Motivation Consider the standard CW-complex, CW-decomposition of the ''n''-sphere, with one zero cell and a single ''n''-cell. From the point of view of smooth manifolds, this is a degenerate decomposition of the sphere, as there is no natural way to see the smooth structure of S^n from the eyes of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topologist
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Misner
Charles W. Misner (; born June 13, 1932) is an American physicist and one of the authors of '' Gravitation''. His specialties include general relativity and cosmology. His work has also provided early foundations for studies of quantum gravity and numerical relativity. Biography Academic training and university positions Misner received his B.S. degree from the University of Notre Dame in 1952. He then moved to Princeton University where he earned an M.A. in 1954 and completed his Ph.D. in 1957. His dissertation, ''Outline of Feynman Quantization of General Relativity; Derivation of Field Equations; Vanishing of the Hamiltonian'', was completed under John Wheeler. Prior to completing his Ph.D., Misner joined the faculty of the Princeton Physics Department with the rank of Instructor (1956–1959), and was subsequently promoted to assistant professor (1959–1963). In 1963 he moved to the University of Maryland, College Park as an associate professor and achieved full p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Archibald Wheeler
John Archibald Wheeler (July 9, 1911April 13, 2008) was an American theoretical physicist. He was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission. Together with Gregory Breit, Wheeler developed the concept of the Breit–Wheeler process. He is best known for popularizing the term "black hole," as to objects with gravitational collapse already predicted during the early 20th century, for inventing the terms "quantum foam", "neutron moderator", "wormhole" and "it from bit", and for hypothesizing the "one-electron universe". Stephen Hawking referred to him as the "hero of the black hole story". Wheeler earned his doctorate at Johns Hopkins University under the supervision of Karl Herzfeld, and studied under Breit and Bohr on a National Research Council fellowship. During 1939 he collaborated with Bohr to write a series of papers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Physicist
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena. The advancement of science generally depends on the interplay between experimental studies and theory. In some cases, theoretical physics adheres to standards of mathematical rigour while giving little weight to experiments and observations.There is some debate as to whether or not theoretical physics uses mathematics to build intuition and illustrativeness to extract physical insight (especially when normal experience fails), rather than as a tool in formalizing theories. This links to the question of it using mathematics in a less formally rigorous, and more intuitive or heuristic way than, say, mathematical physics. For example, while developing special relativity, Albert Einstein was concerned with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stanford Encyclopedia Of Philosophy
The ''Stanford Encyclopedia of Philosophy'' (''SEP'') combines an online encyclopedia of philosophy with peer-reviewed publication of original papers in philosophy, freely accessible to Internet users. It is maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from many academic institutions worldwide. Authors contributing to the encyclopedia give Stanford University the permission to publish the articles, but retain the copyright to those articles. Approach and history As of August 5th, 2022, the ''SEP'' has 1,774 published entries. Apart from its online status, the encyclopedia uses the traditional academic approach of most encyclopedias and academic journals to achieve quality by means of specialist authors selected by an editor or an editorial committee that is competent (although not necessarily considered specialists) in the field covered by the encyclopedia and peer review. The encyclopedia was created in 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Field
An electromagnetic field (also EM field or EMF) is a classical (i.e. non-quantum) field produced by (stationary or moving) electric charges. It is the field described by classical electrodynamics (a classical field theory) and is the classical counterpart to the quantized electromagnetic field tensor in quantum electrodynamics (a quantum field theory). The electromagnetic field propagates at the speed of light (in fact, this field can be identified ''as'' light) and interacts with charges and currents. Its quantum counterpart is one of the four fundamental forces of nature (the others are gravitation, weak interaction and strong interaction.) The field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, and the magnetic field by moving charges (currents); these two are often described as the sources of the field. The way in which charges and currents interact with the electromagnetic field is des ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermann Weyl
Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, he is associated with the University of Göttingen tradition of mathematics, represented by Carl Friedrich Gauss, David Hilbert and Hermann Minkowski. His research has had major significance for theoretical physics as well as purely mathematical disciplines such as number theory. He was one of the most influential mathematicians of the twentieth century, and an important member of the Institute for Advanced Study during its early years. Weyl contributed to an exceptionally wide range of mathematical fields, including works on space, time, matter, philosophy, logic, symmetry and the history of mathematics. He was one of the first to conceive of combining general relativity with the laws of electromagnetism. Freeman Dyson wrote that Weyl alone bore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |