|
Dynamic Time Warping
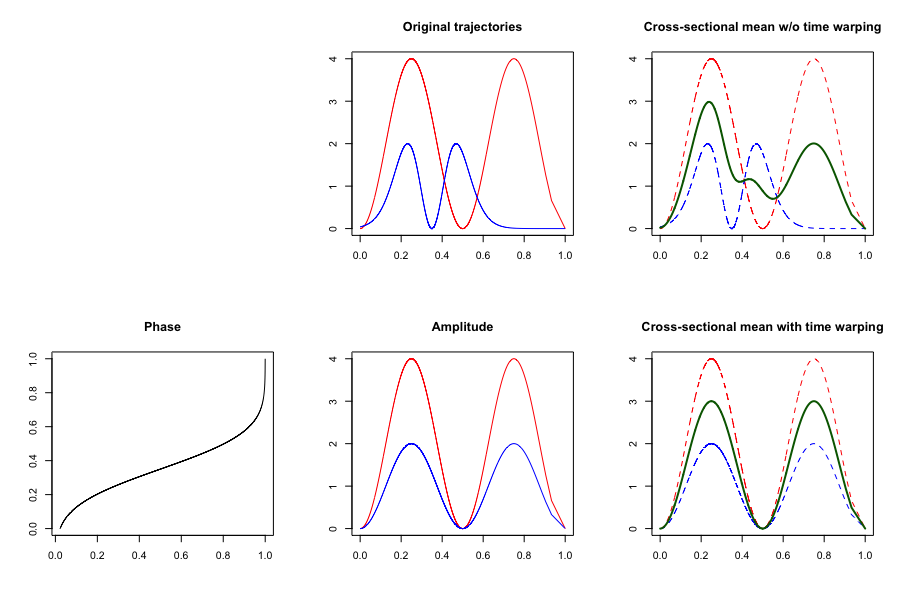
In time series analysis, dynamic time warping (DTW) is an algorithm for measuring similarity between two temporal sequences, which may vary in speed. For instance, similarities in walking could be detected using DTW, even if one person was walking faster than the other, or if there were accelerations and decelerations during the course of an observation. DTW has been applied to temporal sequences of video, audio, and graphics data — indeed, any data that can be turned into a one-dimensional sequence can be analyzed with DTW. A well-known application has been automatic speech recognition, to cope with different speaking speeds. Other applications include speaker recognition and online signature recognition. It can also be used in partial Shape analysis (digital geometry), shape matching applications. In general, DTW is a method that calculates an Optimal matching, optimal match between two given sequences (e.g. time series) with certain restriction and rules: * Every index from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Needleman–Wunsch Algorithm
The Needleman–Wunsch algorithm is an algorithm used in bioinformatics to align protein or nucleotide sequences. It was one of the first applications of dynamic programming to compare biological sequences. The algorithm was developed by Saul B. Needleman and Christian D. Wunsch and published in 1970. The algorithm essentially divides a large problem (e.g. the full sequence) into a series of smaller problems, and it uses the solutions to the smaller problems to find an optimal solution to the larger problem. It is also sometimes referred to as the optimal matching algorithm and the global alignment technique. The Needleman–Wunsch algorithm is still widely used for optimal global alignment, particularly when the quality of the global alignment is of the utmost importance. The algorithm assigns a score to every possible alignment, and the purpose of the algorithm is to find all possible alignments having the highest score. Introduction This algorithm can be used for any two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time Warp Edit Distance
In the data analysis of time series, Time Warp Edit Distance (TWED) is a measure of similarity (or dissimilarity) between pairs of discrete time series, controlling the relative distortion of the time units of the two series using the physical notion of elasticity. In comparison to other distance measures, (e.g. DTW (dynamic time warping) or LCS (longest common subsequence problem)), TWED is a metric. Its computational time complexity is O(n^2), but can be drastically reduced in some specific situations by using a corridor to reduce the search space. Its memory space complexity can be reduced to O(n). It was first proposed in 2009 by P.-F. Marteau. Definition \delta_(A^p_1,B^q_1) = Min \begin \delta_(A^_1,B^q_1) + \Gamma(a^_p \to \Lambda) & \rm \\ \delta_(A^_1,B^_1) + \Gamma(a^_p \to b^_q) & \rm\\ \delta_(A^_1,B^_1) + \Gamma(\Lambda \to b^_q) & \rm \end whereas \Gamma(\alpha^_p \to \Lambda) = d_(a^_, a^_) + \nu \cdot (t_ - t_) + \lambda \Gamma(\alpha^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mlpy
mlpy is a Python, open-source, machine learning library built on top of NumPy/SciPy, the GNU Scientific Library and it makes an extensive use of the Cython language. mlpy provides a wide range of state-of-the-art machine learning methods for supervised and unsupervised problems and it is aimed at finding a reasonable compromise among modularity, maintainability, reproducibility, usability and efficiency. mlpy is multiplatform, it works with Python 2 and 3 and it is distributed under GPL3. Suited for general-purpose machine learning tasks, mlpy's motivating application field is bioinformatics, i.e. the analysis of high throughput omics data. Features * Regression: least squares, ridge regression, least angle regression, elastic net, kernel ridge regression, support vector machines (SVM), partial least squares (PLS) * Classification: linear discriminant analysis (LDA), Basic perceptron, Elastic Net, logistic regression, (Kernel) Support Vector Machines (SVM), Diagonal Linear Discri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nonlinear Mixed-effects Model
Nonlinear mixed-effects models constitute a class of statistical models generalizing linear mixed-effects models. Like linear mixed-effects models, they are particularly useful in settings where there are multiple measurements within the same statistical units or when there are dependencies between measurements on related statistical units. Nonlinear mixed-effects models are applied in many fields including medicine, public health, pharmacology, and ecology. Definition While any statistical model containing both fixed effects and random effects is an example of a nonlinear mixed-effects model, the most commonly used models are members of the class of nonlinear mixed-effects models for repeated measures :_ = f(\phi_,_) + \epsilon_,\quad i =1,\ldots, M, \, j = 1,\ldots, n_i where *M is the number of groups/subjects, *n_i is the number of observations for the ith group/subject, *f is a real-valued differentiable function of a group-specific parameter vector \phi_ and a covariate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM). The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal. His ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hidden Markov Model
A hidden Markov model (HMM) is a Markov model in which the observations are dependent on a latent (or ''hidden'') Markov process (referred to as X). An HMM requires that there be an observable process Y whose outcomes depend on the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about state of X by observing Y. By definition of being a Markov model, an HMM has an additional requirement that the outcome of Y at time t = t_0 must be "influenced" exclusively by the outcome of X at t = t_0 and that the outcomes of X and Y at t < t_0 must be conditionally independent of at given at time . Estimation of the parameters in an HMM can be performed using maximum likelihood estimation. For linear chain HMMs, the Baum–Welch algorithm can be used to estimate parameters. Hidden Markov models are known for their applications to thermodynamics, statistical mechanics, physics, chem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable. Definition Given two differentiable manifolds M and N, a Differentiable manifold#Differentiability of mappings between manifolds, continuously differentiable map f \colon M \rightarrow N is a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. Two C^r-differentiable manifolds are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Radial Basis Function
In mathematics a radial basis function (RBF) is a real-valued function \varphi whose value depends only on the distance between the input and some fixed point, either the origin, so that \varphi(\mathbf) = \hat\varphi(\left\, \mathbf\right\, ), or some other fixed point \mathbf, called a ''center'', so that \varphi(\mathbf) = \hat\varphi(\left\, \mathbf-\mathbf\right\, ). Any function \varphi that satisfies the property \varphi(\mathbf) = \hat\varphi(\left\, \mathbf\right\, ) is a radial function. The distance is usually Euclidean distance, although other metrics are sometimes used. They are often used as a collection \_k which forms a basis for some function space of interest, hence the name. Sums of radial basis functions are typically used to approximate given functions. This approximation process can also be interpreted as a simple kind of neural network; this was the context in which they were originally applied to machine learning, in work by David Broomhead and David Low ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Functional Data Analysis
Functional data analysis (FDA) is a branch of statistics that analyses data providing information about curves, surfaces or anything else varying over a continuum. In its most general form, under an FDA framework, each sample element of functional data is considered to be a random function. The physical continuum over which these functions are defined is often time, but may also be spatial location, wavelength, probability, etc. Intrinsically, functional data are infinite dimensional. The high intrinsic dimensionality of these data brings challenges for theory as well as computation, where these challenges vary with how the functional data were sampled. However, the high or infinite dimensional structure of the data is a rich source of information and there are many interesting challenges for research and data analysis. History Functional data analysis has roots going back to work by Grenander and Karhunen in the 1940s and 1950s. They considered the decomposition of square-integrab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
K-nearest Neighbors Algorithm
In statistics, the ''k''-nearest neighbors algorithm (''k''-NN) is a Non-parametric statistics, non-parametric supervised learning method. It was first developed by Evelyn Fix and Joseph Lawson Hodges Jr., Joseph Hodges in 1951, and later expanded by Thomas M. Cover, Thomas Cover. Most often, it is used for statistical classification, classification, as a ''k''-NN classifier, the output of which is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its ''k'' nearest neighbors (''k'' is a positive integer, typically small). If ''k'' = 1, then the object is simply assigned to the class of that single nearest neighbor. The ''k''-NN algorithm can also be generalized for regression analysis, regression. In ''-NN regression'', also known as ''nearest neighbor smoothing'', the output is the property value for the object. This value is the average of the values of ''k'' nearest neighbo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |