|
Double-pushout Approach
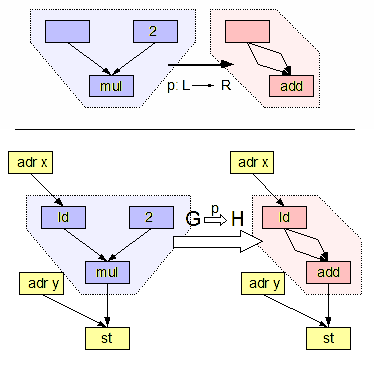
In computer science, double pushout graph rewriting (or DPO graph rewriting) refers to a mathematical framework for graph rewriting. It was introduced as one of the first algebraic approaches to graph rewriting in the article "Graph-grammars: An algebraic approach" (1973). It has since been generalized to allow rewriting structures which are not graphs, and to handle negative application conditions, among other extensions. Definition A DPO graph transformation system (or graph grammar) consists of a finite graph, which is the starting state, and a finite or countable set of labeled spans in the category of finite graphs and graph homomorphisms, which serve as derivation rules. The rule spans are generally taken to be composed of monomorphisms, but the details can vary."Double-pushout graph transformation revisited", Habel, Annegret and Müller, Jürgen and Plump, Detlef, Mathematical Structures in Computer Science, vol. 11, no. 05., pp. 637--688, 2001, Cambridge University Press ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Halting Problem
In computability theory (computer science), computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever. The halting problem is ''Undecidable problem, undecidable'', meaning that no general algorithm exists that solves the halting problem for all possible program–input pairs. The problem comes up often in discussions of computability since it demonstrates that some functions are mathematically Definable set, definable but not Computable function, computable. A key part of the formal statement of the problem is a mathematical definition of a computer and program, usually via a Turing machine. The proof then shows, for any program that might determine whether programs halt, that a "pathological" program exists for which makes an incorrect determination. Specifically, is the program that, when called with some input, passes its own s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Attributed Graph
In computer science, an attributed graph grammar is a class of graph grammar that associates vertices with a set of attributes and rewrites with functions on attributes. In the algebraic approach to graph grammars, they are usually formulated using the double-pushout approach or the single-pushout approach. Implementation AGG, a rule-based visual language that directly expresses attributed graph grammars using the single-pushout approach has been developed at TU Berlin for many years. See also * Graph rewriting * Attribute grammar An attribute grammar is a formal way to supplement a formal grammar with semantic information processing. Semantic information is stored in attributes associated with terminal and nonterminal symbols of the grammar. The values of attributes are t ... Notes References *. *Ehrig, Heckel, Korff, Lowe, Ribeiro, Wagner and Corradini, 1997. Algebraic Approaches to Graph Transformation - Part II: Single Pushout Approach and Comparison with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Typed Graph
Typing is the process of writing or inputting text by pressing keys on a typewriter, computer keyboard, mobile phone, or calculator. It can be distinguished from other means of text input, such as handwriting and speech recognition. Text can be in the form of letters, numbers and other symbols. The world's first typist was Lillian Sholes from Wisconsin in the United States, the daughter of Christopher Latham Sholes, who invented the first practical typewriter. User interface features such as spell checker and autocomplete serve to facilitate and speed up typing and to prevent or correct errors the typist may make. Techniques Hunt and peck Hunt and peck (''two-fingered typing'') is a common form of typing in which the typist presses each key individually. In the purest form of the method, the typist finds each key by sight on the fly, and uses only one or two fingers (typically the index fingers). Although good accuracy may be achieved, the use of this method may also prevent t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hypergraph
In mathematics, a hypergraph is a generalization of a Graph (discrete mathematics), graph in which an graph theory, edge can join any number of vertex (graph theory), vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. Formally, a directed hypergraph is a pair (X,E), where X is a set of elements called ''nodes'', ''vertices'', ''points'', or ''elements'' and E is a set of pairs of subsets of X. Each of these pairs (D,C)\in E is called an ''edge'' or ''hyperedge''; the vertex subset D is known as its ''tail'' or ''domain'', and C as its ''head'' or ''codomain''. The order of a hypergraph (X,E) is the number of vertices in X. The size of the hypergraph is the number of edges in E. The order of an edge e=(D,C) in a directed hypergraph is , e, = (, D, ,, C, ): that is, the number of vertices in its tail followed by the number of vertices in its head. The definition above generalizes from a directed graph to a directed hypergraph by defining the h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coproduct
In category theory, the coproduct, or categorical sum, is a construction which includes as examples the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the "least specific" object to which each object in the family admits a morphism. It is the category-theoretic dual notion to the categorical product, which means the definition is the same as the product but with all arrows reversed. Despite this seemingly innocuous change in the name and notation, coproducts can be and typically are dramatically different from products within a given category. Definition Let C be a category and let X_1 and X_2 be objects of C. An object is called the coproduct of X_1 and X_2, written X_1 \sqcup X_2, or X_1 \oplus X_2, or sometimes simply X_1 + X_2, if there exist morphisms i_1 : X_1 \to X_1 \sqcup X_2 and i_2 : X_2 \to X_1 \sqcup X_2 that satisfies th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Adhesive Category
In mathematics, an adhesive category is a category where pushouts of monomorphisms exist and work more or less as they do in the category of sets. An example of an adhesive category is the category of directed multigraphs, or quivers, and the theory of adhesive categories is important in the theory of graph rewriting. More precisely, an adhesive category is one where any of the following equivalent conditions hold: * ''C'' has all pullbacks, it has pushouts along monomorphisms, and pushout squares of monomorphisms are also pullback squares and are stable under pullback. * ''C'' has all pullbacks, it has pushouts along monomorphisms, and the latter are also (bicategorical) pushouts in the bicategory of spans in ''C''. If ''C'' is small, we may equivalently say that ''C'' has all pullbacks, has pushouts along monomorphisms, and admits a full embedding into a Grothendieck topos In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
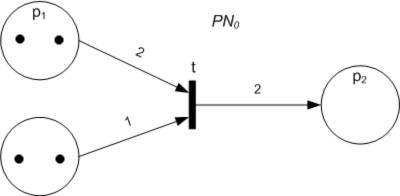
Petri Nets
A Petri net, also known as a place/transition net (PT net), is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements: places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri — at the age of 13 — for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Post Correspondence Problem
The Post correspondence problem is an undecidable decision problem that was introduced by Emil Post in 1946. Because it is simpler than the halting problem In computability theory (computer science), computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run for ... and the ''Entscheidungsproblem'' it is often used in proofs of undecidability. Definition of the problem Let A be an alphabet with at least two symbols. The input of the problem consists of two finite lists \alpha_, \ldots, \alpha_ and \beta_, \ldots, \beta_ of words over A. A solution to this problem is a sequence of indices (i_k)_ with K \ge 1 and 1 \le i_k \le N for all k, such that : \alpha_ \ldots \alpha_ = \beta_ \ldots \beta_. The decision problem then is to decide whether such a solution exists or not. Alternative definition :g: (i_1,\ldots,i_K) \mapsto \alpha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Undecidable Problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether an arbitrary program eventually halts when run. Background A decision problem is a question which, for every input in some infinite set of inputs, requires a "yes" or "no" answer. Those inputs can be numbers (for example, the decision problem "is the input a prime number?") or values of some other kind, such as strings of a formal language. The formal representation of a decision problem is a subset of the natural numbers. For decision problems on natural numbers, the set consists of those numbers that the decision problem answers "yes" to. For example, the decision problem "is the input even?" is formalized as the set of even numbers. A decision pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Concurrency (computer Science)
Concurrency refers to the ability of a system to execute multiple tasks through simultaneous execution or time-sharing (context switching), sharing resources and managing interactions. Concurrency improves responsiveness, throughput, and scalability in modern computing, including: * Operating systems and embedded systems * Distributed systems, parallel computing, and high-performance computing * Database systems, web applications, and cloud computing Related concepts Concurrency is a broader concept that encompasses several related ideas, including: * Parallelism (simultaneous execution on multiple processing units). Parallelism executes tasks independently on multiple CPU cores. Concurrency allows for multiple ''threads of control'' at the program level, which can use parallelism or time-slicing to perform these tasks. Programs may exhibit parallelism only, concurrency only, both parallelism and concurrency, neither. * Multi-threading and multi-processing (shared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Graph Rewriting
In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering ( software construction and also software verification) to layout algorithms and picture generation. Graph transformations can be used as a computation abstraction. The basic idea is that if the state of a computation can be represented as a graph, further steps in that computation can then be represented as transformation rules on that graph. Such rules consist of an original graph, which is to be matched to a subgraph in the complete state, and a replacing graph, which will replace the matched subgraph. Formally, a graph rewriting system usually consists of a set of graph rewrite rules of the form L \rightarrow R, with L being called pattern graph (or left-hand side) and R being called replacement graph (or right-hand side of the rule). A graph rewrite rule is applie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |