|
Dodecahedral Prism
In geometry, a dodecahedral prism is a convex uniform 4-polytope. This 4-polytope has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices. It can be constructed by creating two coinciding dodecahedra in 3-space, and translating each copy in opposite perpendicular directions in 4-space until their separation equals their edge length. It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids. Alternative names # Dodecahedral dyadic prism Norman W. Johnson # Dodecahedral hyperprism Images File:Hyperprisme dodécaèdre.gif File:Dodecahedral hyperprism Schlegel.png , Transparent Schlegel diagram File:Dodecahedral hyperprism.png , An orthographic projection with a wireframe model and has half of the pentagonal faces colored to show the two dodecahedra. The dodecahedra are regular, but look fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedral Prism
In geometry, a dodecahedral prism is a convex uniform 4-polytope. This 4-polytope has 14 polyhedral cells: 2 dodecahedra connected by 12 pentagonal prisms. It has 54 faces: 30 squares and 24 pentagons. It has 80 edges and 40 vertices. It can be constructed by creating two coinciding dodecahedra in 3-space, and translating each copy in opposite perpendicular directions in 4-space until their separation equals their edge length. It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids. Alternative names # Dodecahedral dyadic prism Norman W. Johnson # Dodecahedral hyperprism Images File:Hyperprisme dodécaèdre.gif File:Dodecahedral hyperprism Schlegel.png , Transparent Schlegel diagram File:Dodecahedral hyperprism.png , An orthographic projection with a wireframe model and has half of the pentagonal faces colored to show the two dodecahedra. The dodecahedra are regular, but look fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedral Prism Net
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Poinsot polyhedron, regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The #Pyritohedron, pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the #Tetartoid, tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
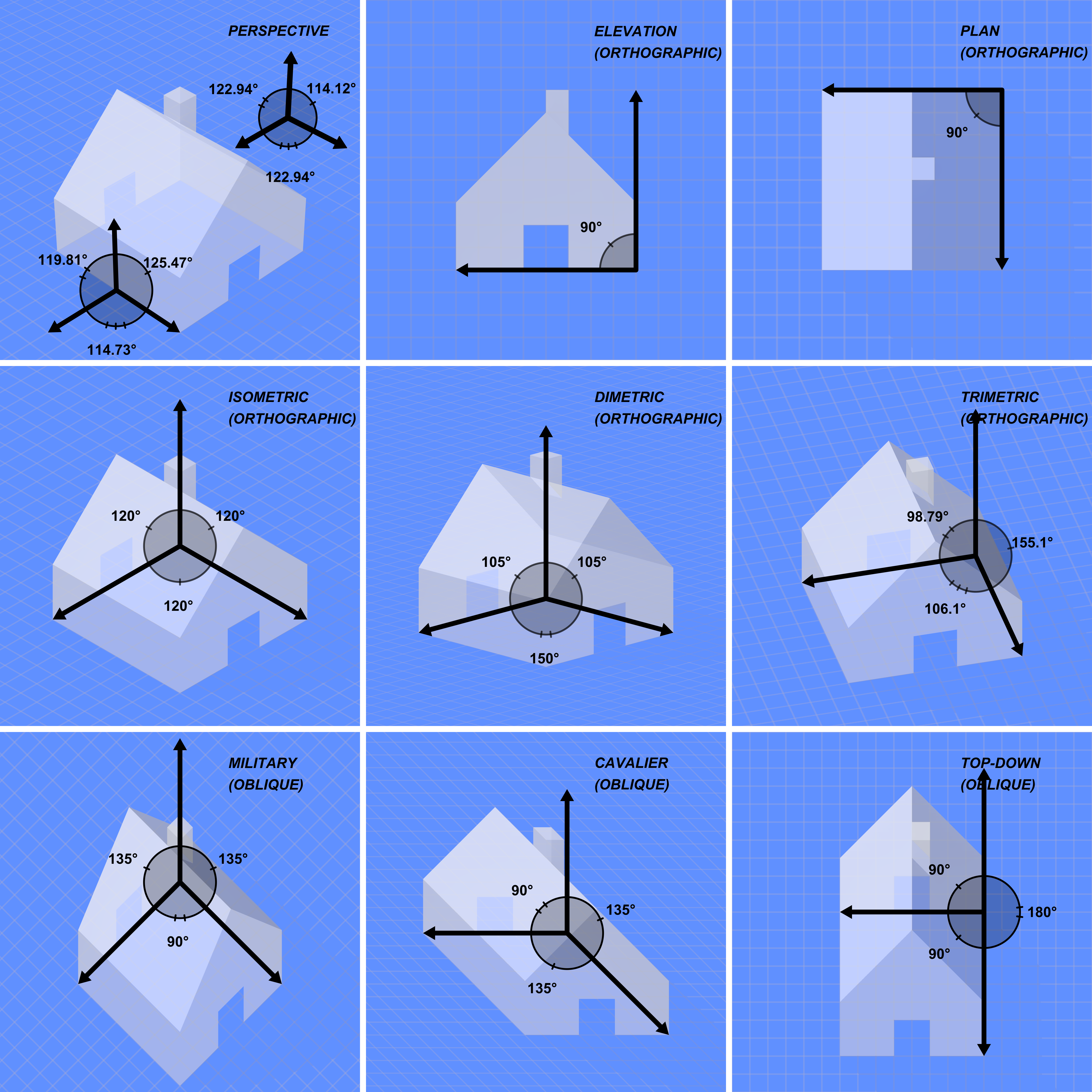
Orthographic Projection (geometry)
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Axonometric projection'' is synonymous with ''par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norman Johnson (mathematician)
Norman Woodason Johnson () was a mathematician at Wheaton College, Norton, Massachusetts. Early life and education Norman Johnson was born on in Chicago. His father had a bookstore and published a local newspaper. Johnson earned his undergraduate mathematics degree in 1953 at Carleton College in Northfield, Minnesota followed by a master's degree from the University of Pittsburgh. After graduating in 1953, Johnson did alternative civilian service as a conscientious objector. He earned his PhD from the University of Toronto in 1966 with a dissertation title of ''The Theory of Uniform Polytopes and Honeycombs'' under the supervision of H. S. M. Coxeter. From there, he accepted a position in the Mathematics Department of Wheaton College in Massachusetts and taught until his retirement in 1998. Career In 1966, he enumerated 92 convex non-uniform polyhedra with regular faces. Victor Zalgaller later proved (1969) that Johnson's list was complete, and the set is now known a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solid
In geometry, an Archimedean solid is one of the 13 solids first enumerated by Archimedes. They are the convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids (which are composed of only one type of polygon), excluding the prisms and antiprisms, and excluding the pseudorhombicuboctahedron. They are a subset of the Johnson solids, whose regular polygonal faces do not need to meet in identical vertices. "Identical vertices" means that each two vertices are symmetric to each other: A global isometry of the entire solid takes one vertex to the other while laying the solid directly on its initial position. observed that a 14th polyhedron, the elongated square gyrobicupola (or pseudo-rhombicuboctahedron), meets a weaker definition of an Archimedean solid, in which "identical vertices" means merely that the faces surrounding each vertex are of the same types (i.e. each vertex looks the same from close up), so only a lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Platonic Solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra: Geometers have studied the Platonic solids for thousands of years. They are named for the ancient Greek philosopher Plato who hypothesized in one of his dialogues, the ''Timaeus'', that the classical elements were made of these regular solids. History The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements. Euclid defined the term in Book XI as “a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms”. However, this definition has been criticized for not being specific enough in relation to the nature of the bases, which caused confusion among later geometry writers. Oblique prism An oblique prism is a pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on the same plane. Cubes and pyramids are examples of convex polyhedra. A polyhedron is a 3-dimensional example of a polytope, a more general concept in any number of dimensions. Definition Convex polyhedra are well-defined, with several equivalent standard definitions. However, the formal mathematical definition of polyhedra that are not required to be convex has been problematic. Many definitions of "polyhedron" have been given within particular contexts,. some more rigorous than others, and there is not universal agreement over which of these to choose. Some of these definitions exclude shapes that have often been counted as polyhedra (such as the self-crossing polyhedra) or include shapes that are often not considered as valid polyhedr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells. The 4-polytopes were discovered by the Swiss mathematician Ludwig Schläfli before 1853. The two-dimensional analogue of a 4-polytope is a polygon, and the three-dimensional analogue is a polyhedron. Topologically 4-polytopes are closely related to the uniform honeycombs, such as the cubic honeycomb, which tessellate 3-space; similarly the 3D cube is related to the infinite 2D square tiling. Convex 4-polytopes can be ''cut and unfolded'' as nets in 3-space. Definition A 4-polytope is a closed four-dimensional figure. It comprises vertices (corner points), edges, faces and cells. A cell is the three-dimensional analogue of a face, and is therefore a polyhedron. Each fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons. There are 47 non-prismatic convex uniform 4-polytopes. There are two infinite sets of convex prismatic forms, along with 17 cases arising as prisms of the convex uniform polyhedra. There are also an unknown number of non-convex star forms. History of discovery * Convex Regular polytopes: ** 1852: Ludwig Schläfli proved in his manuscript ''Theorie der vielfachen Kontinuität'' that there are exactly 6 regular polytopes in 4 dimensions and only 3 in 5 or more dimensions. * Regular star 4-polytopes (star polyhedron cells and/or vertex figures) ** 1852: Ludwig Schläfli also found 4 of the 10 regular star 4-polytopes, discounting 6 with cells or vertex figures and . ** 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) ''Einleitung in die Leh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set contained in the n-dimensional Euclidean space \mathbb^n. Most texts. use the term "polytope" for a bounded convex polytope, and the word "polyhedron" for the more general, possibly unbounded object. Others''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> (including this article) allow polytopes to be unbounded. The terms "bounded/unbounded convex polytope" will be used below whenever the boundedness is critical to the discussed issue. Yet other texts identify a convex polytope with its boundary. Convex polytopes play an important role both in various branches of mathematics and in applied areas, most notably in linear programming. In the influential textbooks of Grünbaum and Ziegler on the subject, as well as in many other texts in discrete geometry, convex polytopes are often simply called "polytopes". Grünbaum points out that this is solely to avoi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |