|
Discriminant (other)
{{Mathematical disambiguation ...
The discriminant of a polynomial is a quantity that depends on the coefficients and determines various properties of the roots. Discriminant may also refer to its various generalizations: Mathematics *Discriminant of an algebraic number field * Discriminant of an elliptic curve * Discriminant of a quadratic form * Discriminant of a real-valued function * Fundamental discriminant * Modular discriminant Medicine *Modified Maddrey's discriminant function Psychology * Discriminant validity Statistics * Discriminant analysis *Kernel Fisher discriminant analysis *Multiple discriminant analysis Multiple Discriminant Analysis (MDA) is a multivariate dimensionality reduction technique. It has been used to predict signals as diverse as neural memory traces and corporate failure. MDA is not directly used to perform classification. It merel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the polynomial has three distinct real roots, and negative i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Of An Algebraic Number Field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the (ring of integers of the) algebraic number field. More specifically, it is proportional to the squared volume of the fundamental domain of the ring of integers, and it regulates which primes are ramified. The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic formulas such as the functional equation of the Dedekind zeta function of ''K'', and the analytic class number formula for ''K''. A theorem of Hermite states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem, and the subject of current research. The discriminant of ''K'' can be referred to as the absolute discriminant of ''K'' to distinguish it from the relative discriminant of an extension ''K''/''L'' of number fields. The latter is an ideal in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliptic Curve
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point . An elliptic curve is defined over a field and describes points in , the Cartesian product of with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which consists of solutions for: :y^2 = x^3 + ax + b for some coefficients and in . The curve is required to be non-singular, which means that the curve has no cusps or self-intersections. (This is equivalent to the condition , that is, being square-free in .) It is always understood that the curve is really sitting in the projective plane, with the point being the unique point at infinity. Many sources define an elliptic curve to be simply a curve given by an equation of this form. (When the coefficient field has characteristic 2 or 3, the above equation is not quite general enough to include all non-singular cubic cu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and allows deducing some properties of the roots without computing them. More precisely, it is a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry. The discriminant of the quadratic polynomial ax^2+bx+c is :b^2-4ac, the quantity which appears under the square root in the quadratic formula. If a\ne 0, this discriminant is zero if and only if the polynomial has a double root. In the case of real coefficients, it is positive if the polynomial has two distinct real roots, and negative if it has two distinct complex conjugate roots. Similarly, the discriminant of a cubic polynomial is zero if and only if the polynomial has a multiple root. In the case of a cubic with real coefficients, the discriminant is positive if the polynomial has three distinct real roots, and negative i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hessian Matrix
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". Definitions and properties Suppose f : \R^n \to \R is a function taking as input a vector \mathbf \in \R^n and outputting a scalar f(\mathbf) \in \R. If all second-order partial derivatives of f exist, then the Hessian matrix \mathbf of f is a square n \times n matrix, usually defined and arranged as follows: \mathbf H_f= \begin \dfrac & \dfrac & \cdots & \dfrac \\ .2ex \dfrac & \dfrac & \cdots & \dfrac \\ .2ex \vdots & \vdots & \ddots & \vdots \\ .2ex \dfrac & \dfrac & \cdots & \dfrac \end, or, by stating an equation for the coefficients using indices i and j, (\mathbf H_f)_ = \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Discriminant
In mathematics, a fundamental discriminant ''D'' is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of ''Q''(''x'', ''y''). Conversely, every integer ''D'' with is the discriminant of some binary quadratic form with integer coefficients. Thus, all such integers are referred to as ''discriminants'' in this theory. There are explicit congruence conditions that give the set of fundamental discriminants. Specifically, ''D'' is a fundamental discriminant if and only if one of the following statements holds * ''D'' ≡ 1 (mod 4) and is square-free, * ''D'' = 4''m'', where ''m'' ≡ 2 or 3 (mod 4) and ''m'' is square-free. The first ten positive fundamental discriminants are: : 1, 5, 8, 12, 13, 17, 21, 24, 28, 29, 33 . The first ten negative fundamental discriminants are: : −3, −4, −7, −8, −11, −15, −19, −20, −23, −24, −31 . Connection with quadratic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass's Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Definition Let \omega_1,\omega_2\in\mathbb be two complex numbers that are linearly independent over \mathbb and let \Lambda:=\mathbb\omega_1+\mathbb\omega_2:=\ be the lattice generated by those numbers. Then the \wp-function is defined as follows: \weierp(z,\omega_1,\omega_2):=\weierp(z,\Lambda) := \frac + \sum_\left(\frac 1 - \frac 1 \right). This series converges locally uniformly absolutely in \math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Maddrey's Discriminant Function
Maddrey's discriminant function (DF) is the traditional model for evaluating the severity and prognosis in alcoholic hepatitis and evaluates the efficacy of using alcoholic hepatitis steroid treatment. The Maddrey DF score is a predictive statistical model compares the subject's DF score with mortality prognosis within 30-day or 90-day scores. The subject's Maddrey DF score is determined by blood analysis. The modified Maddrey's discriminant function was originally described by Maddrey and Boitnott to predict prognosis in alcoholic hepatitis. It is calculated by a simple formula using prothrombin time and serum bilirubin Bilirubin (BR) (Latin for "red bile") is a red-orange compound that occurs in the normal catabolic pathway that breaks down heme in vertebrates. This catabolism is a necessary process in the body's clearance of waste products that arise from the ... concentration: \left(4.6 \times \left(\hbox - \hbox\right)\right) + \hbox Prospective studies have shown t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminant Validity
In psychology, discriminant validity tests whether concepts or measurements that are not supposed to be related are actually unrelated. Campbell and Fiske (1959) introduced the concept of discriminant validity within their discussion on evaluating test validity. They stressed the importance of using both discriminant and Convergent validity, convergent validation techniques when assessing new tests. A successful evaluation of discriminant validity shows that a test of a concept is not highly correlated with other tests designed to measure theoretically different concepts. In showing that two scales do not correlate, it is necessary to correct for attenuation in the correlation due to measurement error. It is possible to calculate the extent to which the two scales overlap by using the following formula where r_ is correlation between x and y, r_ is the reliability of x, and r_ is the reliability of y: :\cfrac Although there is no standard value for discriminant validity, a result ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
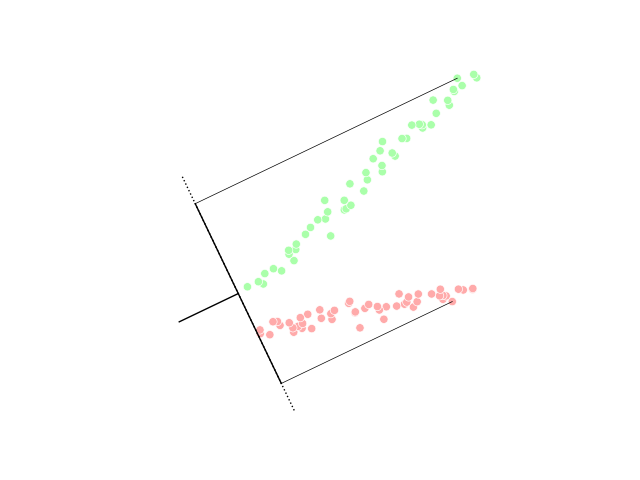
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical independent variables and a continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more similar to LDA than ANOVA is, as they also explain a categorical var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Fisher Discriminant Analysis
In statistics, kernel Fisher discriminant analysis (KFD), also known as generalized discriminant analysis and kernel discriminant analysis, is a kernelized version of linear discriminant analysis (LDA). It is named after Ronald Fisher. Linear discriminant analysis Intuitively, the idea of LDA is to find a projection where class separation is maximized. Given two sets of labeled data, \mathbf_1 and \mathbf_2, we can calculate the mean value of each class, \mathbf_1 and \mathbf_2, as : \mathbf_i = \frac\sum_^\mathbf_n^i, where l_i is the number of examples of class \mathbf_i. The goal of linear discriminant analysis is to give a large separation of the class means while also keeping the in-class variance small. This is formulated as maximizing, with respect to \mathbf, the following ratio: : J(\mathbf) = \frac, where \mathbf_B is the between-class covariance matrix and \mathbf_W is the total within-class covariance matrix: : \begin \mathbf_B & = (\mathbf_2-\mathbf_1)(\mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |