|
Dihedral Angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes. The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes (commonly called wings) are upwardly inclined to the lateral axis. When downwardly inclined they are said to be at a negative dihedral angle. Mathematical background When the two intersecting planes are described in terms of Cartesian coordinates by the two equations : a_1 x + b_1 y + c_1 z + d_1 = 0 :a_2 x + b_2 y + c_2 z + d_2 = 0 the dihedral angle, \varphi between them is given by: :\cos \varphi = \frac and satisfies 0\le \varphi \le \pi/2. Alternatively, if an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Angle
A dihedral angle is the angle between two intersecting planes or half-planes. In chemistry, it is the clockwise angle between half-planes through two sets of three atoms, having two atoms in common. In solid geometry, it is defined as the union of a line and two half-planes that have this line as a common edge. In higher dimensions, a dihedral angle represents the angle between two hyperplanes. The planes of a flying machine are said to be at positive dihedral angle when both starboard and port main planes (commonly called wings) are upwardly inclined to the lateral axis. When downwardly inclined they are said to be at a negative dihedral angle. Mathematical background When the two intersecting planes are described in terms of Cartesian coordinates by the two equations : a_1 x + b_1 y + c_1 z + d_1 = 0 :a_2 x + b_2 y + c_2 z + d_2 = 0 the dihedral angle, \varphi between them is given by: :\cos \varphi = \frac and satisfies 0\le \varphi \le \pi/2. Alternatively, if an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amino Acid
Amino acids are organic compounds that contain both amino and carboxylic acid functional groups. Although hundreds of amino acids exist in nature, by far the most important are the alpha-amino acids, which comprise proteins. Only 22 alpha amino acids appear in the genetic code. Amino acids can be classified according to the locations of the core structural functional groups, as Alpha and beta carbon, alpha- , beta- , gamma- or delta- amino acids; other categories relate to Chemical polarity, polarity, ionization, and side chain group type (aliphatic, Open-chain compound, acyclic, aromatic, containing hydroxyl or sulfur, etc.). In the form of proteins, amino acid ''residues'' form the second-largest component ( water being the largest) of human muscles and other tissues. Beyond their role as residues in proteins, amino acids participate in a number of processes such as neurotransmitter transport and biosynthesis. It is thought that they played a key role in enabling li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bond
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force and hydrogen bonding. Strong chemical bonding arises from the sharing or transfer of electrons between the participating atoms. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. An electron positioned between two nuclei will be attracted to both of them, and the nuclei will be attracted toward electrons in this position. This attraction co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereochemistry
Stereochemistry, a subdiscipline of chemistry, involves the study of the relative spatial arrangement of atoms that form the structure of molecules and their manipulation. The study of stereochemistry focuses on the relationships between stereoisomers, which by definition have the same molecular formula and sequence of bonded atoms (constitution), but differ in structural formula (the three-dimensional orientations of their atoms in space). For this reason, it is also known as 3D chemistry—the prefix "stereo-" means "three-dimensionality". Stereochemistry spans the entire spectrum of organic, inorganic, biological, physical and especially supramolecular chemistry. Stereochemistry includes methods for determining and describing these relationships; the effect on the physical or biological properties these relationships impart upon the molecules in question, and the manner in which these relationships influence the reactivity of the molecules in question (dynamic stereochem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
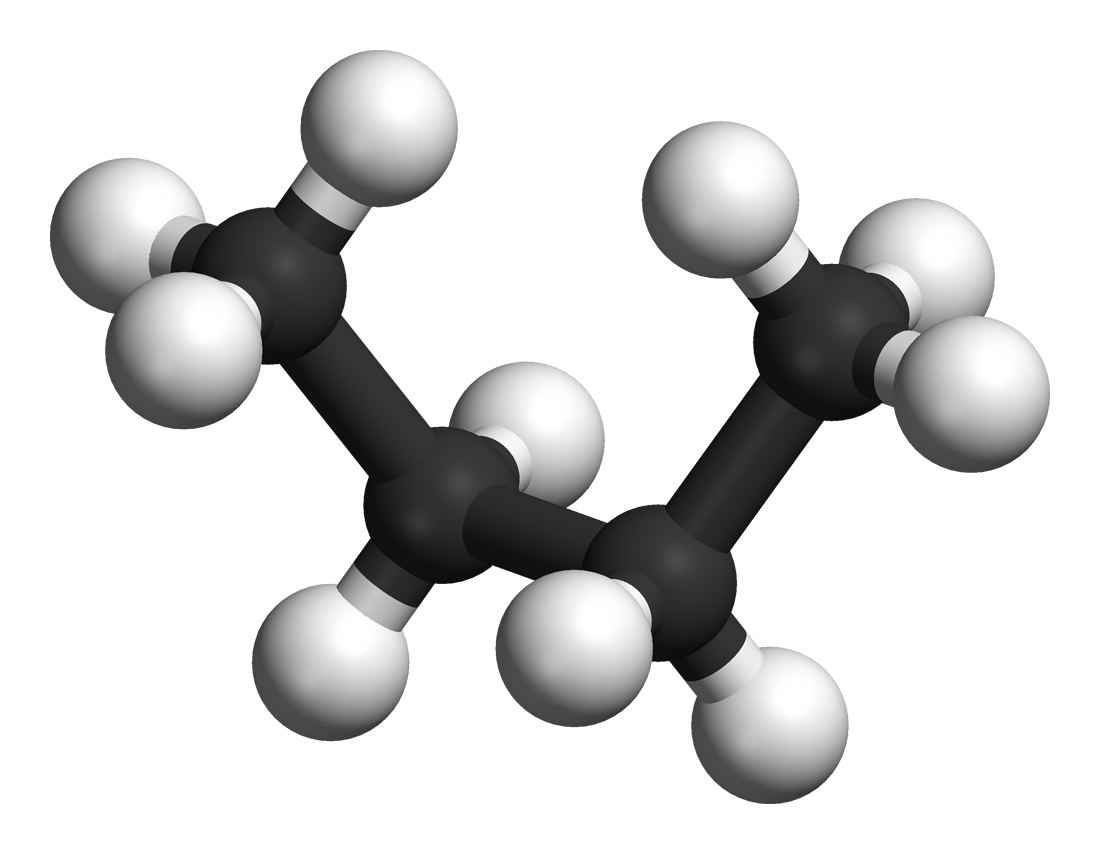
Dihedral Angles Of Butane , a geometric shape
{{ ...
Dihedral or polyhedral may refer to: * Dihedral angle, the angle between two mathematical planes * Dihedral (aeronautics), the upward angle of a fixed-wing aircraft's wings where they meet at the fuselage, dihedral ''effect'' of an aircraft, longitudinal dihedral angle of a fixed-wing aircraft * Dihedral group, the group of symmetries of the ''n''-sided polygon in abstract algebra ** Also Dihedral symmetry in three dimensions * Dihedral kite, also known as a bowed kite * Dihedral doors, also known as butterfly doors * Dihedral prime, also known as a dihedral calculator prime * In rock climbing, an inside corner of rock See also * Anhedral (other) * Euhedral, a crystal structure * Polyhedron In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices. A convex polyhedron is the convex hull of finitely many points, not all on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newman Projection
A Newman projection is a drawing that helps visualize the 3-dimensional structure of a molecule. This projection most commonly sights down a carbon-carbon bond, making it a very useful way to visualize the stereochemistry of alkanes. A Newman projection visualizes the conformation of a chemical bond from front to back, with the front atom represented by the intersection of three lines (a dot) and the back atom as a circle. The front atom is called ''proximal'', while the back atom is called ''distal''. This type of representation clearly illustrates the specific dihedral angle between the proximal and distal atoms. This projection is named after American chemist Melvin Spencer Newman, who introduced it in 1952 as a partial replacement for Fischer projections, which are unable to represent conformations and thus conformers properly.Newman, MS. ''Record. Chem. Progr. (Kresge-Hooker Sci. Lib.) 1952,'' 13'', 111'' This diagram style is an alternative to a sawhorse projection, wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butane
Butane () or ''n''-butane is an alkane with the formula C4H10. Butane is a gas at room temperature and atmospheric pressure. Butane is a highly flammable, colorless, easily liquefied gas that quickly vaporizes at room temperature. The name butane comes from the root but- (from butyric acid, named after the Greek word for butter) and the suffix -ane. It was discovered by the chemist Dr. Walter Snelling in 1912. It was found dissolved in crude petroleum in 1864 by Edmund Ronalds, who was the first to describe its properties. Butane is one of a group of liquefied petroleum gases (LP gases). The others include propane, propylene, butadiene, butylene, isobutylene, and mixtures thereof. Butane burns more cleanly than gasoline and coal. Density The density of butane is highly dependent on temperature and pressure in the reservoir. For example, the density of liquid phase is 571.8±1 kg/m3 (for pressures up to 2MPa and temperature 27±0.2 °C), while the density o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sawhorse Projection Butane -sc
In woodworking, a saw-horse or sawhorse (saw-buck, trestle, buck) is a trestle structure used to support a board or plank for sawing. A pair of sawhorses can support a plank, forming a scaffold. In certain circles, it is also known as a '' mule'' and a short sawhorse is known as a pony. The names come from the shape of the frame, which resembles a horse. A sawhorse may also be a rack for supporting logs for sawing, known in the US as a sawbuck. The sawhorse may be designed to fold for storage. A sawhorse with a wide top is particularly useful to support a board for sawing or as a field workbench, and is more useful as a single, but also more difficult to store. A sawhorse can also be used as the base for a portable work table by placing a sheet of plywood or even a door across two sawhorses. If the sawhorses are strong enough, the portable table can be used as a platform for tools like a table saw, although with caution if the top is not secured to the sawhorses. In boatm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newman Projection Butane -sc
Newman is a surname of English origin and may refer to many people: The surname Newman is widespread in the core Anglosphere. A * Abram Newman (1736–1799), British grocer * Adrian Newman (other), multiple people *Al Newman (born 1960), American baseball player * Alan Newman (baseball) (born 1969), American baseball player * Alec Newman (born 1974), Scottish actor * Alfred Newman (other), multiple people * Ali Newman (born 1977), better known as Brother Ali, American rapper * Alison Newman (born 1968), British actress *Allen George Newman (1875–1940), American sculptor *Alysha Newman (born 1994), Canadian pole vaulter * Amy Hauck Newman, American medicinal chemist *Andrea Newman (1938–2019), British author *Andrew Newman (other), multiple people * Angelia Thurston Newman (1837–1910), American poet and writer *Anne B. Newman (born 1955), American gerontologist *Arnold Newman (1918–2006), American photographer * Aubrey Newman (1903–1994), Ame ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross Product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is denoted by the symbol \times. Given two linearly independent vectors and , the cross product, (read "a cross b"), is a vector that is perpendicular to both and , and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product (projection product). If two vectors have the same direction or have the exact opposite direction from each other (that is, they are ''not'' linearly independent), or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Triple Product
In geometry and algebra, the triple product is a product of three 3- dimensional vectors, usually Euclidean vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product. Scalar triple product The scalar triple product (also called the mixed product, box product, or triple scalar product) is defined as the dot product of one of the vectors with the cross product of the other two. Geometric interpretation Geometrically, the scalar triple product : \mathbf\cdot(\mathbf\times \mathbf) is the (signed) volume of the parallelepiped defined by the three vectors given. Here, the parentheses may be omitted without causing ambiguity, since the dot product cannot be evaluated first. If it were, it would leave the cross product of a scalar and a vector, which is not defined. Properties * The scalar triple product is unchanged under a circular shift of its three operands (a, b, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
