|
Decision Tree Complexity
In computational complexity the decision tree model is the model of computation in which an algorithm is considered to be basically a decision tree, i.e., a sequence of ''queries'' or ''tests'' that are done adaptively, so the outcome of the previous tests can influence the test is performed next. Typically, these tests have a small number of outcomes (such as a yes–no question) and can be performed quickly (say, with unit computational cost), so the worst-case time complexity of an algorithm in the decision tree model corresponds to the depth of the corresponding decision tree. This notion of computational complexity of a problem or an algorithm in the decision tree model is called its decision tree complexity or query complexity. Decision trees models are instrumental in establishing lower bounds for complexity theory for certain classes of computational problems and algorithms. Several variants of decision tree models have been introduced, depending on the computational mode ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). One of the roles of computationa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Las Vegas Algorithm
In computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. However, the runtime of a Las Vegas algorithm differs depending on the input. The usual definition of a Las Vegas algorithm includes the restriction that the ''expected'' runtime be finite, where the expectation is carried out over the space of random information, or entropy, used in the algorithm. An alternative definition requires that a Las Vegas algorithm always terminates (is effective), but may output a symbol not part of the solution space to indicate failure in finding a solution. The nature of Las Vegas algorithms makes them suitable in situations where the number of possible solutions is limited, and where verifying the correctness of a candidate solution is relatively easy while finding a solution is complex. Las Vegas algorithms are prominent in the field of artificial intelligence, and in other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Complexity Theory
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm. A problem is regarded as inherently difficult if its solution requires significant resources, whatever the algorithm used. The theory formalizes this intuition, by introducing mathematical models of computation to study these problems and quantifying their computational complexity, i.e., the amount of resources needed to solve them, such as time and storage. Other measures of complexity are also used, such as the amount of communication (used in communication complexity), the number of gates in a circuit (used in circuit complexity) and the number of processors (used in parallel computing). One of the roles of computationa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minimum Spanning Tree
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components. There are many use cases for minimum spanning trees. One example is a telecommunications company trying to lay cable in a new neighborhood. If it is constrained to bury the cable only along certain paths (e.g. roads), then there would be a graph containing the points (e.g. houses) connected by those paths. Some of the paths might be more expensive, because they are longer, or require the cable to be buried deeper; these paths would be represented by edges with larger weights ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aanderaa–Karp–Rosenberg Conjecture
In theoretical computer science, the Aanderaa–Karp–Rosenberg conjecture (also known as the Aanderaa–Rosenberg conjecture or the evasiveness conjecture) is a group of related conjectures about the number of questions of the form "Is there an edge between vertex u and vertex v?" that have to be answered to determine whether or not an undirected graph has a particular property such as planarity or bipartiteness. They are named after Stål Aanderaa, Richard M. Karp, and Arnold L. Rosenberg. According to the conjecture, for a wide class of properties, no algorithm can guarantee that it will be able to skip any questions: any algorithm for determining whether the graph has the property, no matter how clever, might need to examine every pair of vertices before it can give its answer. A property satisfying this conjecture is called evasive. More precisely, the Aanderaa–Rosenberg conjecture states that any deterministic algorithm must test at least a constant fraction of all pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
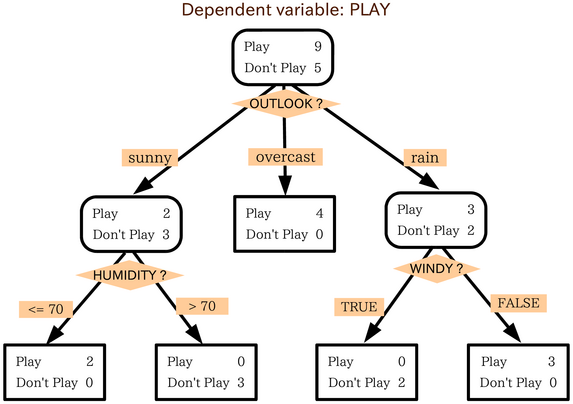
Decision Tree
A decision tree is a decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements. Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in machine learning. Overview A decision tree is a flowchart-like structure in which each internal node represents a "test" on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules. In decision analysis, a decision tree and the closely related influence diagram are used as a visual and analytical decision support tool, where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation (often a "less than or equal to" operator or a three-way comparison) that determines which of two elements should occur first in the final sorted list. The only requirement is that the operator forms a total preorder over the data, with: # if ''a'' ≤ ''b'' and ''b'' ≤ ''c'' then ''a'' ≤ ''c'' (transitivity) # for all ''a'' and ''b'', ''a'' ≤ ''b'' or ''b'' ≤ ''a'' ( connexity). It is possible that both ''a'' ≤ ''b'' and ''b'' ≤ ''a''; in this case either may come first in the sorted list. In a stable sort, the input order determines the sorted order in this case. A metaphor for thinking about comparison sorts is that someone has a set of unlabelled weights and a balance scale. Their goal is to line up the weights in order by their weight without any information except that obtained by placing two weights on the scale and seeing which one i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Emory University
Emory University is a private research university in Atlanta, Georgia. Founded in 1836 as "Emory College" by the Methodist Episcopal Church and named in honor of Methodist bishop John Emory, Emory is the second-oldest private institution of higher education in Georgia. Emory University has nine academic divisions: Emory College of Arts and Sciences, Oxford College, Goizueta Business School, Laney Graduate School, School of Law, School of Medicine, Nell Hodgson Woodruff School of Nursing, Rollins School of Public Health, and the Candler School of Theology. Emory University, the Georgia Institute of Technology, and Peking University in Beijing, China jointly administer the Wallace H. Coulter Department of Biomedical Engineering. The university operates the Confucius Institute in Atlanta in partnership with Nanjing University. Emory has a growing faculty research partnership with the Korea Advanced Institute of Science and Technology (KAIST). Emory University students ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hao Huang (mathematician)
Hao Huang is a mathematician known for solving the sensitivity conjecture. Huang is currently an associate professor in the mathematics department at National University of Singapore. Huang was an assistant professor from 2015 to 2021 in the Department of Mathematics at Emory University. He obtained his Ph.D in mathematics from UCLA in 2012 advised by Benny Sudakov. His postdoctoral research was done at the Institute for Advanced Study in Princeton and DIMACS at Rutgers University in 2012-2014, followed by a year at the Institute for Mathematics and its Applications at University of Minnesota. In July 2019, Huang announced a breakthrough, which gave a proof of the sensitivity conjecture. At that point the conjecture had been open for nearly 30 years, having been posed by Noam Nisan and Mario Szegedy in 1992. Theoretical computer scientist Scott Aaronson said of Huang's ingenious two-page proof, "I find it hard to imagine that even God knows how to prove the Sensitivity Conjecture ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Boolean Functions
In mathematics and theoretical computer science, analysis of Boolean functions is the study of real-valued functions on \^n or \^n (such functions are sometimes known as pseudo-Boolean functions) from a spectral perspective. The functions studied are often, but not always, Boolean-valued, making them Boolean functions. The area has found many applications in combinatorics, social choice theory, random graphs, and theoretical computer science, especially in hardness of approximation, property testing, and PAC learning. Basic concepts We will mostly consider functions defined on the domain \^n. Sometimes it is more convenient to work with the domain \^n instead. If f is defined on \^n, then the corresponding function defined on \^n is :f_(x_1,\ldots,x_n) = f((-1)^,\ldots,(-1)^). Similarly, for us a Boolean function is a \-valued function, though often it is more convenient to consider \-valued functions instead. Fourier expansion Every real-valued function f\colon \^n \to \mathbb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Function
In mathematics, a partial function from a set to a set is a function from a subset of (possibly itself) to . The subset , that is, the domain of viewed as a function, is called the domain of definition of . If equals , that is, if is defined on every element in , then is said to be total. More technically, a partial function is a binary relation over two sets that associates every element of the first set to ''at most'' one element of the second set; it is thus a functional binary relation. It generalizes the concept of a (total) function by not requiring every element of the first set to be associated to ''exactly'' one element of the second set. A partial function is often used when its exact domain of definition is not known or difficult to specify. This is the case in calculus, where, for example, the quotient of two functions is a partial function whose domain of definition cannot contain the zeros of the denominator. For this reason, in calculus, and more ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
