|
David Fairlie
David B. Fairlie (born in South Queensferry, Scotland, 1935) is a British mathematician and theoretical physicist, Professor Emeritus at the University of Durham (UK). He was educated in mathematical physics at the University of Edinburgh (BSc 1957), and he earned a PhD at the University of Cambridge in 1960, under the supervision of John Polkinghorne. After postdoctoral training at Princeton University and Cambridge, he was lecturer in St. Andrews (1962–64) and at Durham University (1964), retiring as Professor (2000). He has made numerous influential contributions in particle and mathematical physics, notably in the early formulation of string theory, as well as the determination of the weak mixing angle in extra dimensions, infinite-dimensional Lie algebras, classical solutions of gauge theories, higher-dimensional gauge theories, and deformation quantization. He has co-authored several volumes, notablyThomas L Curtright, David B Fairlie, Cosmas K Zachos, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change. History One of the earliest known mathematicians were Thales of Miletus (c. 624–c.546 BC); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem. The number of known mathematicians grew when Pythagoras of Samos (c. 582–c. 507 BC) established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman mathematician recorded by history was Hypati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
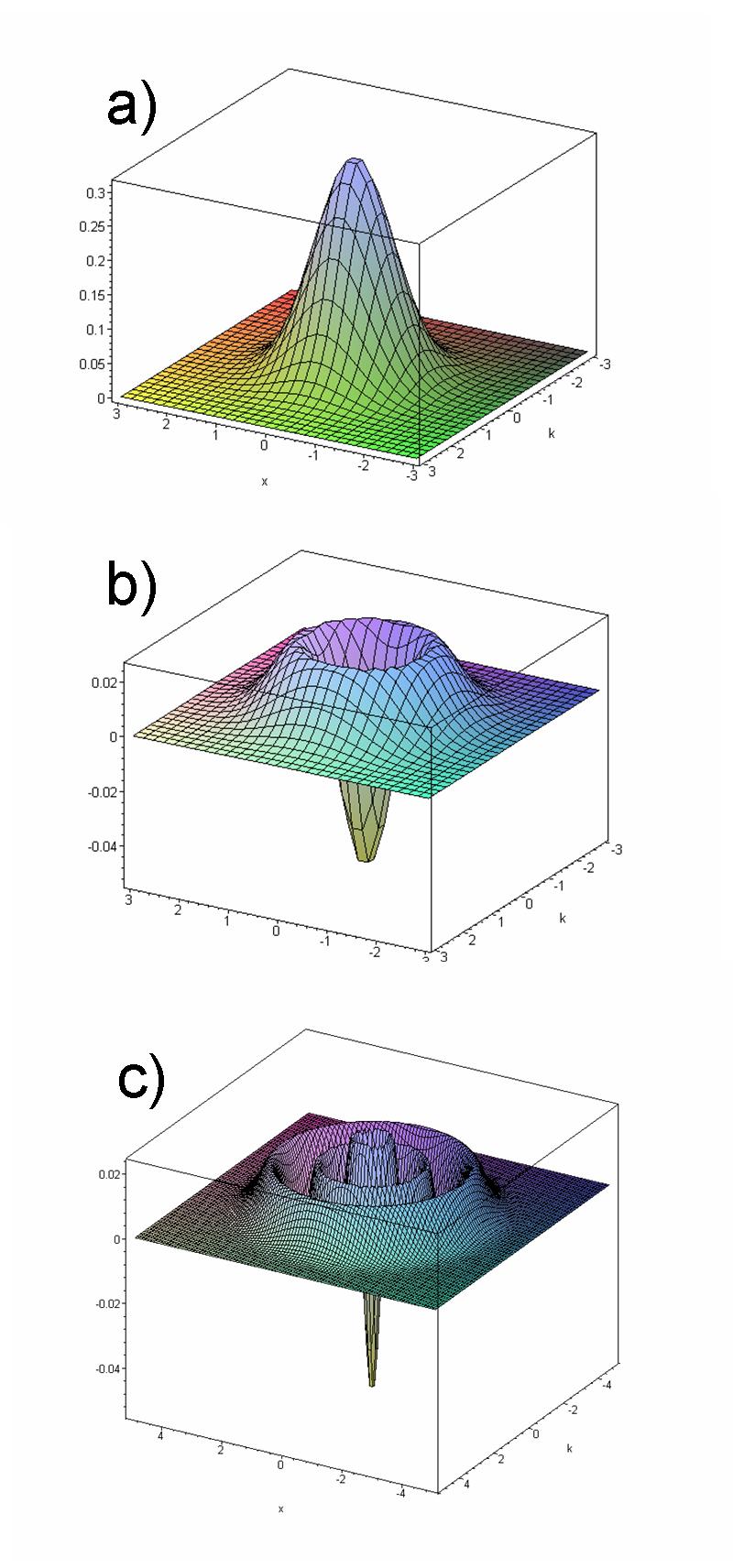
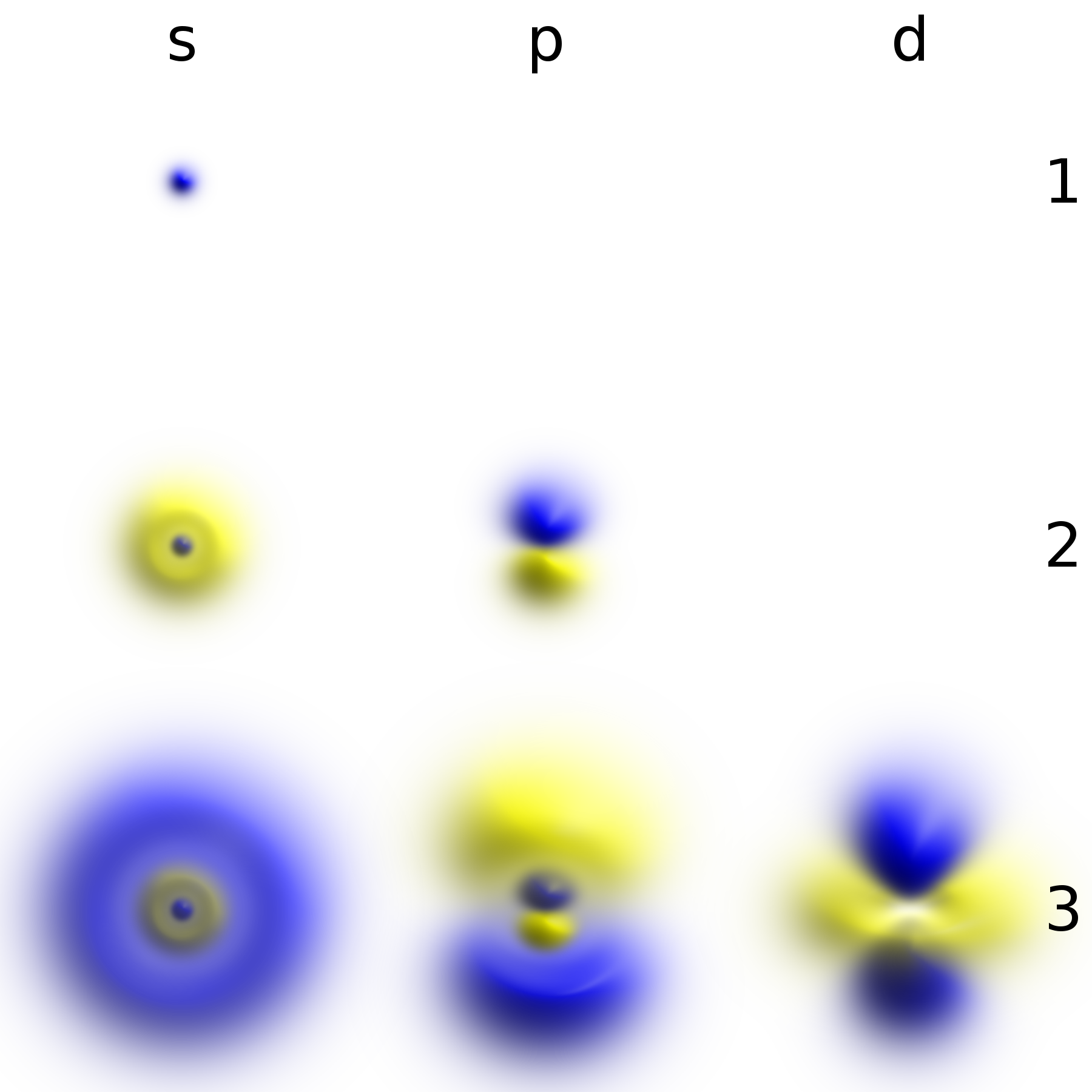
Phase Space Formulation
The phase-space formulation of quantum mechanics places the position ''and'' momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position ''or'' momentum representations (see also position and momentum space). The two key features of the phase-space formulation are that the quantum state is described by a quasiprobability distribution (instead of a wave function, state vector, or density matrix) and operator multiplication is replaced by a star product. The theory was fully developed by Hilbrand Groenewold in 1946 in his PhD thesis, and independently by Joe Moyal, each building on earlier ideas by Hermann Weyl and Eugene Wigner. The chief advantage of the phase-space formulation is that it makes quantum mechanics appear as similar to Hamiltonian mechanics as possible by avoiding the operator formalism, thereby "'freeing' the quantization of the 'burden' of the Hilbert space". This formulation is statistical in nature and offers l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Physicists
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Living People
Related categories * :Year of birth missing (living people) / :Year of birth unknown * :Date of birth missing (living people) / :Date of birth unknown * :Place of birth missing (living people) / :Place of birth unknown * :Year of death missing / :Year of death unknown * :Date of death missing / :Date of death unknown * :Place of death missing / :Place of death unknown * :Missing middle or first names See also * :Dead people * :Template:L, which generates this category or death years, and birth year and sort keys. : {{DEFAULTSORT:Living people 21st-century people People by status ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
British Physicists
British may refer to: Peoples, culture, and language * British people, nationals or natives of the United Kingdom, British Overseas Territories, and Crown Dependencies. ** Britishness, the British identity and common culture * British English, the English language as spoken and written in the United Kingdom or, more broadly, throughout the British Isles * Celtic Britons, an ancient ethno-linguistic group * Brittonic languages, a branch of the Insular Celtic language family (formerly called British) ** Common Brittonic, an ancient language Other uses *'' Brit(ish)'', a 2018 memoir by Afua Hirsch *People or things associated with: ** Great Britain, an island ** United Kingdom, a sovereign state ** Kingdom of Great Britain (1707–1800) ** United Kingdom of Great Britain and Ireland (1801–1922) See also * Terminology of the British Isles * Alternative names for the British * English (other) * Britannic (other) * British Isles * Brit (other) * Briton ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alumni Of The University Of Edinburgh
This is a list of notable graduates as well as non-graduate former students, academic staff, and university officials of the University of Edinburgh in Scotland. It also includes those who may be considered alumni by extension, having studied at institutions that later merged with the University of Edinburgh. The university is associated with 19 Nobel Prize laureates, three Turing Award winners, an Abel Prize laureate and Fields Medallist, four Pulitzer Prize winners, three Prime Ministers of the United Kingdom, and several Olympic gold medallists. Government and politics Heads of state and government United Kingdom Cabinet and Party Leaders Scottish Cabinet and Party Leaders Current Members of the House of Commons * Wendy Chamberlain, MP for North East Fife * Joanna Cherry, MP for Edinburgh South West * Colin Clark, MP for Gordon * Anneliese Dodds, MP for Oxford East * Kate Green, MP for Stretford and Urmston * John Howell, MP for Henley * Neil Hudson, M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alumni Of The University Of Cambridge
Alumni (singular: alumnus (masculine) or alumna (feminine)) are former students of a school, college, or university who have either attended or graduated in some fashion from the institution. The feminine plural alumnae is sometimes used for groups of women. The word is Latin and means "one who is being (or has been) nourished". The term is not synonymous with "graduate"; one can be an alumnus without graduating ( Burt Reynolds, alumnus but not graduate of Florida State, is an example). The term is sometimes used to refer to a former employee or member of an organization, contributor, or inmate. Etymology The Latin noun ''alumnus'' means "foster son" or "pupil". It is derived from PIE ''*h₂el-'' (grow, nourish), and it is a variant of the Latin verb ''alere'' "to nourish".Merriam-Webster: alumnus .. Separate, but from the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1935 Births
Events January * January 7 – Italian premier Benito Mussolini and French Foreign Minister Pierre Laval conclude Franco-Italian Agreement of 1935, an agreement, in which each power agrees not to oppose the other's colonial claims. * January 12 – Amelia Earhart becomes the first person to successfully complete a solo flight from Hawaii to California, a distance of 2,408 miles. * January 13 – A plebiscite in the Saar (League of Nations), Territory of the Saar Basin shows that 90.3% of those voting wish to join Germany. * January 24 – The first canned beer is sold in Richmond, Virginia, United States, by Gottfried Krueger Brewing Company. February * February 6 – Parker Brothers begins selling the board game Monopoly (game), Monopoly in the United States. * February 13 – Richard Hauptmann is convicted and sentenced to death for the kidnapping and murder of Charles Lindbergh Jr. in the United States. * February 15 – The discovery and clinical development of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually consists of all possible values of position and momentum variables. It is the outer product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Introduction In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-space trajectory for the system) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Curtright
Thomas L. Curtright (born 1948) is a theoretical physicist at the University of Miami. He did undergraduate work in physics at the University of Missouri (B.S., M.S., 1970), and graduate work at Caltech (Ph.D., 1977) under the supervision of Richard Feynman. He has made numerous influential contributions in particle and mathematical physics, notably in supercurrent anomalies, higher-spin fields (Curtright field), quantum Liouville theory, geometrostatic sigma models, quantum algebras, and deformation quantization. Curtright is a Fellow of the American Physical Society, a co-recipient (with Charles Thorn) of the SESAPS Jesse Beams Award, a University of Miami Cooper Fellow, and a recipient of the Distinguished Faculty Scholar Award from the University's Senate. He is also the recipient of Distinguished Alumni Awards from the Department of Physics and Astronomy (2021) and from the College of Arts and Science (2022), University of Missouri at Columbia. He has co-edited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |