|
Dark State
In atomic physics, a dark state refers to a state of an atom or molecule that cannot absorb (or emit) photons. All atoms and molecules are described by quantum states; different states can have different energies and a system can make a transition from one energy level to another by emitting or absorbing one or more photons. However, not all transitions between arbitrary states are allowed. A state that cannot absorb an incident photon is called a dark state. This can occur in experiments using laser light to induce transitions between energy levels, when atoms can spontaneously decay into a state that is not coupled to any other level by the laser light, preventing the atom from absorbing or emitting light from that state. A dark state can also be the result of quantum interference in a three-level system, when an atom is in a coherent superposition of two states, both of which are coupled by lasers at the right frequency to a third state. With the system in a particular superpo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. Atomic physics typically refers to the study of atomic structure and the interaction between atoms. It is primarily concerned with the way in which electrons are arranged around the nucleus and the processes by which these arrangements change. This comprises ions, neutral atoms and, unless otherwise stated, it can be assumed that the term ''atom'' includes ions. The term ''atomic physics'' can be associated with nuclear power and nuclear weapons, due to the synonymous use of ''atomic'' and ''nuclear'' in standard English. Physicists distinguish between atomic physics—which deals with the atom as a system consisting of a nucleus and electrons—and nuclear physics, which studies nuclear reactions and special properties of atomic nuclei. As with many scientific fields, strict delineation can be highly contrived and atomic physics is often considered in the wider c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Laser Articles
This is a list of laser topics. A * 3D printing, additive manufacturing * Abnormal reflection * Above-threshold ionization * Absorption spectroscopy * Accelerator physics * Acoustic microscopy * Acousto-optic deflector * Acousto-optic modulator * Acousto-optical spectrometer * Acousto-optics * Active laser medium * Active optics * Advanced Precision Kill Weapon System * Advanced Tactical Laser * Afocal system * Airborne laser * Airborne wind turbine * Airy beam * ALKA * All gas-phase iodine laser * Ambient ionization * Amplified spontaneous emission * Analytical chemistry * Aneutronic fusion * Antiproton Decelerator * Apache Arrowhead * Apache Point Observatory Lunar Laser-ranging Operation * Arago spot * Argon fluoride laser * Argus laser * Asterix IV laser * Astrophysical maser * Atmospheric-pressure laser ionization * Atom interferometer * Atom laser * Atom probe * Atomic clock * Atomic coherence * Atomic fountain * Atomic line filter * Atomic ratio * Atomic spectros ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetically Induced Transparency
Electromagnetically induced transparency (EIT) is a coherent optical nonlinearity which renders a medium transparent within a narrow spectral range around an absorption line. Extreme dispersion is also created within this transparency "window" which leads to "slow light", described below. It is in essence a quantum interference effect that permits the propagation of light through an otherwise opaque atomic medium. Observation of EIT involves two optical fields (highly coherent light sources, such as lasers) which are tuned to interact with three quantum states of a material. The "probe" field is tuned near resonance between two of the states and measures the absorption spectrum of the transition. A much stronger "coupling" field is tuned near resonance at a different transition. If the states are selected properly, the presence of the coupling field will create a spectral "window" of transparency which will be detected by the probe. The coupling laser is sometimes referred t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated by t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Conjugate
In mathematics, specifically in operator theory, each linear operator A on a Euclidean vector space defines a Hermitian adjoint (or adjoint) operator A^* on that space according to the rule :\langle Ax,y \rangle = \langle x,A^*y \rangle, where \langle \cdot,\cdot \rangle is the inner product on the vector space. The adjoint may also be called the Hermitian conjugate or simply the Hermitian after Charles Hermite. It is often denoted by in fields like physics, especially when used in conjunction with bra–ket notation in quantum mechanics. In finite dimensions where operators are represented by matrices, the Hermitian adjoint is given by the conjugate transpose (also known as the Hermitian transpose). The above definition of an adjoint operator extends verbatim to bounded linear operators on Hilbert spaces H. The definition has been further extended to include unbounded '' densely defined'' operators whose domain is topologically dense in—but not necessarily equal to� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
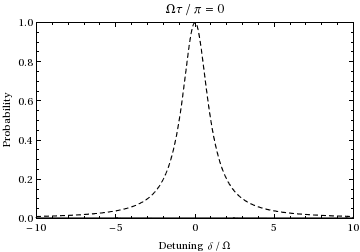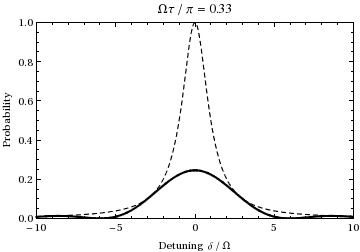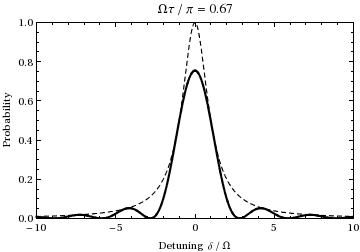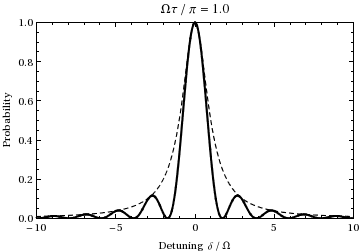
Rabi Frequency
The Rabi frequency is the frequency at which the probability amplitudes of two atomic energy levels fluctuate in an oscillating electromagnetic field. It is proportional to the Transition Dipole Moment of the two levels and to the amplitude (''not'' intensity) of the Electromagnetic field. Population transfer between the levels of such a 2-level system illuminated with light exactly resonant with the difference in energy between the two levels will occur at the Rabi frequency; when the incident light is detuned from this energy difference (detuned from resonance) then the population transfer occurs at the generalized Rabi frequency. The Rabi frequency is a semiclassical concept since it treats the atom as an object with quantized energy levels and the electromagnetic field as a continuous wave. In the context of a nuclear magnetic resonance experiment, the Rabi frequency is the nutation frequency of a sample's net nuclear magnetization vector about a radio-frequency field. (Not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) Hamilton may refer to: People * Hamilton (name), a common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotating Wave Approximation
The rotating-wave approximation is an approximation used in atom optics and magnetic resonance. In this approximation, terms in a Hamiltonian that oscillate rapidly are neglected. This is a valid approximation when the applied electromagnetic radiation is near resonance with an atomic transition, and the intensity is low. Explicitly, terms in the Hamiltonians that oscillate with frequencies \omega_L + \omega_0 are neglected, while terms that oscillate with frequencies \omega_L - \omega_0 are kept, where \omega_L is the light frequency, and \omega_0 is a transition frequency. The name of the approximation stems from the form of the Hamiltonian in the interaction picture, as shown below. By switching to this picture the evolution of an atom due to the corresponding atomic Hamiltonian is absorbed into the system ket, leaving only the evolution due to the interaction of the atom with the light field to consider. It is in this picture that the rapidly oscillating terms mentioned previ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metastable State
In chemistry and physics, metastability denotes an intermediate energetic state within a dynamical system other than the system's state of least energy. A ball resting in a hollow on a slope is a simple example of metastability. If the ball is only slightly pushed, it will settle back into its hollow, but a stronger push may start the ball rolling down the slope. Bowling pins show similar metastability by either merely wobbling for a moment or tipping over completely. A common example of metastability in science is isomerisation. Higher energy isomers are long lived because they are prevented from rearranging to their preferred ground state by (possibly large) barriers in the potential energy. During a metastable state of finite lifetime, all state-describing parameters reach and hold stationary values. In isolation: *the state of least energy is the only one the system will inhabit for an indefinite length of time, until more external energy is added to the system (unique "ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and biochemistry, the distinction from ions is dropped and ''molecule'' is often used when referring to polyatomic ions. A molecule may be homonuclear, that is, it consists of atoms of one chemical element, e.g. two atoms in the oxygen molecule (O2); or it may be heteronuclear, a chemical compound composed of more than one element, e.g. water (two hydrogen atoms and one oxygen atom; H2O). In the kinetic theory of gases, the term ''molecule'' is often used for any gaseous particle regardless of its composition. This relaxes the requirement that a molecule contains two or more atoms, since the noble gases are individual atoms. Atoms and complexes connected by non-covalent interactions, such as hydrogen bonds or ionic bonds, are typically not consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Selection Rules
In physics and chemistry, a selection rule, or transition rule, formally constrains the possible transitions of a system from one quantum state to another. Selection rules have been derived for electromagnetic transitions in molecules, in atoms, in atomic nuclei, and so on. The selection rules may differ according to the technique used to observe the transition. The selection rule also plays a role in chemical reactions, where some are formally spin-forbidden reactions, that is, reactions where the spin state changes at least once from reactants to products. In the following, mainly atomic and molecular transitions are considered. Overview In quantum mechanics the basis for a spectroscopic selection rule is the value of the ''transition moment integral'' :\int \psi_1^* \, \mu \, \psi_2 \, \mathrm\tau\,, where \psi_1 and \psi_2 are the wave functions of the two states, "state 1" and "state 2", involved in the transition, and is the transition moment operator. This ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png)