|
Dirac Fermion
In physics, a Dirac fermion is a spin-½ particle (a fermion) which is different from its antiparticle. The vast majority of fermions – perhaps all – fall under this category. Description In particle physics, all fermions in the standard model have distinct antiparticles (''perhaps'' excepting neutrinos) and hence are Dirac fermions. They are named after Paul Dirac, and can be modeled with the Dirac equation. A Dirac fermion is equivalent to two Weyl fermions. The counterpart to a Dirac fermion is a Majorana fermion, a particle that must be its own antiparticle. Dirac quasi-particles In condensed matter physics, low-energy excitations in graphene and topological insulators, among others, are fermionic quasiparticles described by a pseudo-relativistic Dirac equation. See also * Dirac spinor, a wavefunction-like description of a Dirac fermion * Dirac–Kähler fermion, a geometric formulation of Dirac fermions * Majorana fermion, an alternate category of fermion, possibly d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." Physics is one of the most fundamental scientific disciplines, with its main goal being to understand how the universe behaves. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Majorana Fermion
A Majorana fermion (, uploaded 19 April 2013, retrieved 5 October 2014; and also based on the pronunciation of physicist's name.), also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles. With the exception of neutrinos, all of the Standard Model fermions are known to behave as Dirac fermions at low energy (lower than the electroweak symmetry breaking temperature), and none are Majorana fermions. The nature of the neutrinos is not settled – they may turn out to be either Dirac or Majorana fermions. In condensed matter physics, quasiparticle excitations can appear like bound Majorana fermions. However, instead of a single fundamental particle, they are the collective movement of several individual particles (themselves composite) which are governed by non-Abelian statisti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac–Kähler Equation
In theoretical physics, the Dirac–Kähler equation, also known as the Ivanenko–Landau–Kähler equation, is the geometric analogue of the Dirac equation that can be defined on any pseudo-Riemannian manifold using the Laplace–de Rham operator. In four-dimensional flat spacetime, it is equivalent to four copies of the Dirac equation that transform into each other under Lorentz transformations, although this is no longer true in curved spacetime. The geometric structure gives the equation a natural discretization that is equivalent to the staggered fermion formalism in lattice field theory, making Dirac–Kähler fermions the formal continuum limit of staggered fermions. The equation was discovered by Dmitri Ivanenko and Lev Landau in 1928 and later rediscovered by Erich Kähler in 1962. Mathematical overview In four dimensional Euclidean spacetime a generic fields of differential forms : \Phi = \sum_ \Phi_H(x)dx_H, is written as a linear combination of sixteen basis for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Spinor
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group. Dirac spinors are important and interesting in numerous ways. Foremost, they are important as they do describe all of the known fundamental particle fermions in nature; this includes the electron and the quarks. Algebraically they behave, in a certain sense, as the "square root" of a vector. This is not readily apparent from direct examination, but it has slowly become clear over the last 60 years that spinorial representations are fundamental to geometry. For example, effectively all Riemannian manifolds can have spinors and spin connections built upon them, via the Clifford algebra. The Dirac spinor is specific to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiparticle
In physics, quasiparticles and collective excitations are closely related emergent phenomena arising when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in vacuum. For example, as an electron travels through a semiconductor, its motion is disturbed in a complex way by its interactions with other electrons and with atomic nuclei. The electron behaves as though it has a different effective mass travelling unperturbed in vacuum. Such an electron is called an ''electron quasiparticle''. In another example, the aggregate motion of electrons in the valence band of a semiconductor or a hole band in a metal behave as though the material instead contained positively charged quasiparticles called ''electron holes''. Other quasiparticles or collective excitations include the ''phonon'', a quasiparticle derived from the vibrations of atoms in a solid, and the ''plasmons'', a particle derived from plasma oscillation. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
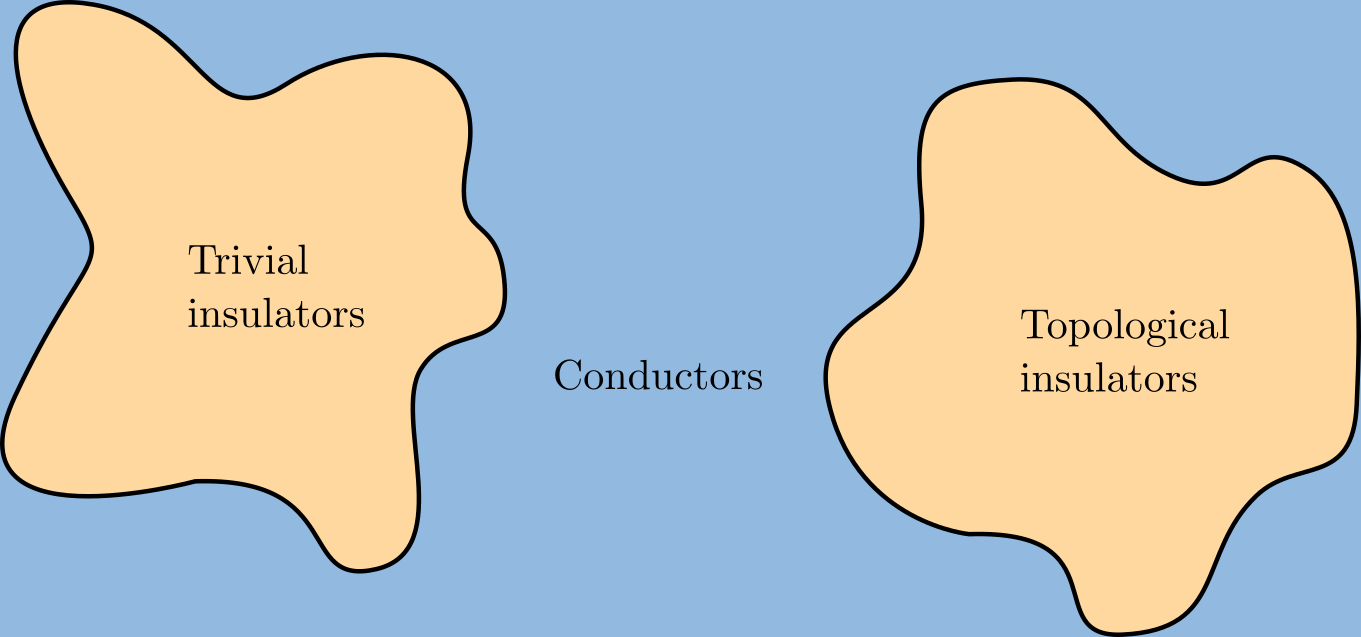
Topological Insulator
A topological insulator is a material whose interior behaves as an electrical insulator while its surface behaves as an electrical conductor, meaning that electrons can only move along the surface of the material. A topological insulator is an insulator for the same reason a " trivial" (ordinary) insulator is: there exists an energy gap between the valence and conduction bands of the material. But in a topological insulator, these bands are, in an informal sense, "twisted", relative to a trivial insulator. The topological insulator cannot be continuously transformed into a trivial one without untwisting the bands, which closes the band gap and creates a conducting state. Thus, due to the continuity of the underlying field, the border of a topological insulator with a trivial insulator (including vacuum, which is topologically trivial) is forced to support a conducting state. Since this results from a global property of the topological insulator's band structure, local (sym ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphene
Graphene () is an allotrope of carbon consisting of a Single-layer materials, single layer of atoms arranged in a hexagonal lattice nanostructure. "Carbon nanostructures for electromagnetic shielding applications", Mohammed Arif Poothanari, Sabu Thomas, et al., ''Industrial Applications of Nanomaterials'', 2019. "Carbon nanostructures include various low-dimensional allotropes of carbon including carbon black (CB), carbon fiber, carbon nanotubes (CNTs), fullerene, and graphene." The name is derived from "graphite" and the suffix -ene, reflecting the fact that the graphite allotrope of carbon contains numerous double bonds. Each atom in a graphene sheet is connected to its three nearest neighbors by a strong σ-bond, and contributes to a valence band one electron that extends over the whole sheet. This is the same type of b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models. The diversity of systems and phenomena available for study makes condensed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl Fermion
Hermann Klaus Hugo Weyl, (; 9 November 1885 – 8 December 1955) was a German mathematician, theoretical physicist and philosopher. Although much of his working life was spent in Zürich, Switzerland, and then Princeton, New Jersey, he is associated with the University of Göttingen tradition of mathematics, represented by Carl Friedrich Gauss, David Hilbert and Hermann Minkowski. His research has had major significance for theoretical physics as well as purely mathematical disciplines such as number theory. He was one of the most influential mathematicians of the twentieth century, and an important member of the Institute for Advanced Study during its early years. Weyl contributed to an exceptionally wide range of mathematical fields, including works on space, time, matter, philosophy, logic, symmetry and the history of mathematics. He was one of the first to conceive of combining general relativity with the laws of electromagnetism. Freeman Dyson wrote that Weyl alone bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin-½
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of . The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of means that the particle must be rotated by two full turns (through 720°) before it has the same configuration as when it started. Particles having net spin include the proton, neutron, electron, neutrino, and quarks. The dynamics of spin- objects cannot be accurately described using classical physics; they are among the simplest systems which require quantum mechanics to describe them. As such, the study of the behavior of spin- systems forms a central part of quantum mechanics. Stern–Gerlach experiment The necessity of introducing half-integer spin goes back experimentally to the results of the Stern–Gerlach experiment. A beam of atoms is run through a strong heterogeneous magnetic field, which then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin- massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, ''antimatter'', previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a ''theoretical'' justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Dirac
Paul Adrien Maurice Dirac (; 8 August 1902 – 20 October 1984) was an English theoretical physicist who is regarded as one of the most significant physicists of the 20th century. He was the Lucasian Professor of Mathematics at the University of Cambridge, a professor of physics at Florida State University and the University of Miami, and a 1933 Nobel Prize recipient. Dirac made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics. Among other discoveries, he formulated the Dirac equation which describes the behaviour of fermions and predicted the existence of antimatter. Dirac shared the 1933 Nobel Prize in Physics with Erwin Schrödinger "for the discovery of new productive forms of atomic theory". He also made significant contributions to the reconciliation of general relativity with quantum mechanics. Dirac was regarded by his friends and colleagues as unusual in character. In a 1926 letter to Paul Ehrenfest, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.gif)
