|
Dini's Surface
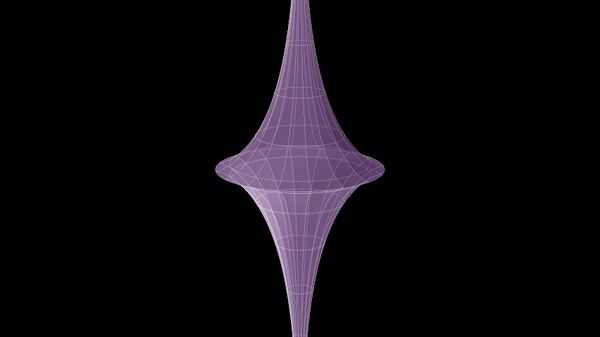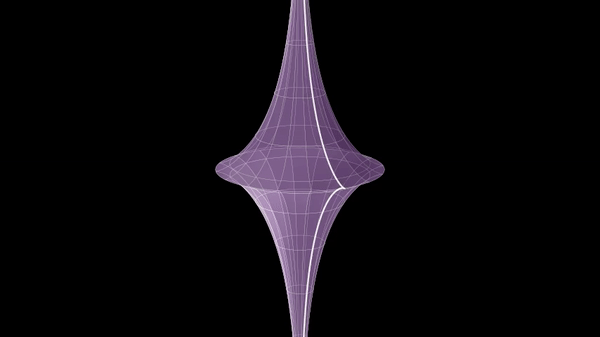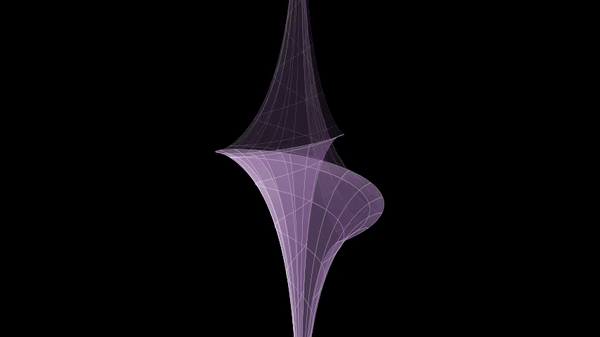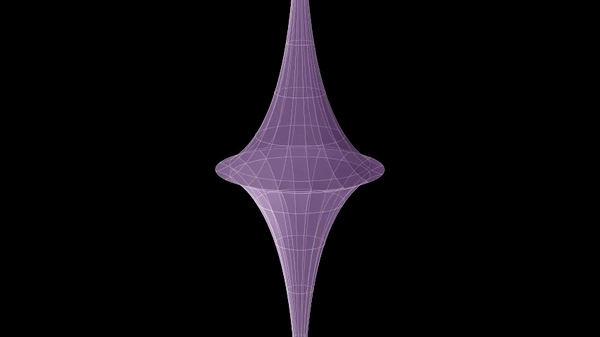
In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere. It is named after Ulisse Dini and described by the following parametric equations: : \begin x&=a \cos u \sin v \\ y&=a \sin u \sin v \\ z&=a \left(\cos v +\ln \tan \frac \right) + bu \end Another description is a generalized helicoid constructed from the tractrix In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angl .... See also * Breather surface References {{reflist Surfaces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematica Dinis Surface
Wolfram Mathematica is a software system with built-in libraries for several areas of technical computing that allow machine learning, statistics, symbolic computation, data manipulation, network analysis, time series analysis, NLP, optimization, plotting functions and various types of data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other programming languages. It was conceived by Stephen Wolfram, and is developed by Wolfram Research of Champaign, Illinois. The Wolfram Language is the programming language used in ''Mathematica''. Mathematica 1.0 was released on June 23, 1988 in Champaign, Illinois and Santa Clara, California. __TOC__ Notebook interface Wolfram Mathematica (called ''Mathematica'' by some of its users) is split into two parts: the kernel and the front end. The kernel interprets expressions (Wolfram Language code) and returns result expressions, which can then be displayed by the front end. The orig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dini Surface
Dini may refer to: Organizations *National Directorate of Intelligence (Peru), the primary intelligence agency in Peru Places in Iran *Ala ol Dini-ye Olya, a village in Eslamabad Rural District, in the Central District of Jiroft County, Kerman Province *Nur ol Dini,a village in Kheyrgu Rural District, Alamarvdasht District, Lamerd County, Fars Province *Tang-e Baha ol Dini, a village in Howmeh Rural District, in the Central District of Larestan County, Fars Province * Tolombeh-ye Rokn ol Dini, a village in Arzuiyeh Rural District, in the Central District of Arzuiyeh County, Kerman Province *Zeyn ol Dini, a village in Kal Rural District, Eshkanan District, Lamerd County, Fars Province People *Abdi Dini (born 1981), professional Canadian wheelchair basketball player *Abdulkadir Sheikh Dini, Somali politician and military officia *Ahmed Dini Ahmed (1932-2004), Djiboutian politician *Andrea Dini (born 1996), Italian football player *Antonio Dini (1918–1940), New Zealand flying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface (mathematics)
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line. There are several more precise definitions, depending on the context and the mathematical tools that are used for the study. The simplest mathematical surfaces are planes and spheres in the Euclidean 3-space. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a topological space of dimension two; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a '' coordinate patch'' on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles (i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surfac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudosphere
In geometry, a pseudosphere is a surface with constant negative Gaussian curvature. A pseudosphere of radius is a surface in \mathbb^3 having curvature in each point. Its name comes from the analogy with the sphere of radius , which is a surface of curvature . The term was introduced by Eugenio Beltrami in his 1868 paper on models of hyperbolic geometry. __TOC__ Tractroid The same surface can be also described as the result of revolving a tractrix about its asymptote. For this reason the pseudosphere is also called tractroid. As an example, the (half) pseudosphere (with radius 1) is the surface of revolution of the tractrix parametrized by :t \mapsto \left( t - \tanh, \operatorname\, \right), \quad \quad 0 \le t < \infty. It is a singular space (the equator is a singularity), but away from the singularities, it has constant negative |
Ulisse Dini
Ulisse Dini (14 November 1845 – 28 October 1918) was an Italian mathematician and politician, born in Pisa. He is known for his contribution to real analysis, partly collected in his book "''Fondamenti per la teorica delle funzioni di variabili reali''". Life and academic career Dini attended the Scuola Normale Superiore in order to become a teacher. One of his professors was Enrico Betti. In 1865, a scholarship enabled him to visit Paris, where he studied under Charles Hermite as well as Joseph Bertrand, and published several papers. In 1866, he was appointed to the University of Pisa, where he taught algebra and geodesy. In 1871, he succeeded Betti as professor for analysis and geometry. From 1888 until 1890, Dini was ''rettore'' of the Pisa University, and of the '' Scuola Normale Superiore'' from 1908 until his death in 1918. He was also active as a politician: in 1871 he was voted into the Pisa city council, and in 1880, he became a member of the Italian parliament. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Equation
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization (alternatively spelled as parametrisation) of the object. For example, the equations :\begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where ''t'' is the parameter: A point (''x'', ''y'') is on the unit circle if and only if there is a value of ''t'' such that these two equations generate that point. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors: :(x, y)=(\cos t, \sin t). Parametric representations are generally nonunique (see the "Examples in two dimensions" section ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dini's Surface
In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere. It is named after Ulisse Dini and described by the following parametric equations: : \begin x&=a \cos u \sin v \\ y&=a \sin u \sin v \\ z&=a \left(\cos v +\ln \tan \frac \right) + bu \end Another description is a generalized helicoid constructed from the tractrix In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angl .... See also * Breather surface References {{reflist Surfaces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Helicoid
In geometry, a generalized helicoid is a surface in Euclidean space generated by rotating and simultaneously displacing a curve, the ''profile curve'', along a line, its ''axis''. Any point of the given curve is the starting point of a circular helix. If the profile curve is contained in a plane through the axis, it is called the meridian of the generalized helicoid. Simple examples of generalized helicoids are the helicoids. The meridian of a helicoid is a line which intersects the axis orthogonally. Essential types of generalized helicoids are * ruled generalized helicoids. Their profile curves are lines and the surfaces are ruled surfaces. *circular generalized helicoids. Their profile curves are circles. In mathematics helicoids play an essential role as minimal surfaces. In the technical area generalized helicoids are used for staircases, slides, screws, and pipes. Analytical representation Screw motion of a point Moving a point on a screwtype curve means, the point i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tractrix
In geometry, a tractrix (; plural: tractrices) is the curve along which an object moves, under the influence of friction, when pulled on a horizontal plane by a line segment attached to a pulling point (the ''tractor'') that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of pursuit. It was first introduced by Claude Perrault in 1670, and later studied by Isaac Newton (1676) and Christiaan Huygens (1693). Mathematical derivation Suppose the object is placed at (or in the example shown at right), and the puller at the origin, so is the length of the pulling thread (4 in the example at right). Then the puller starts to move along the axis in the positive direction. At every moment, the thread will be tangent to the curve described by the object, so that it becomes completely determined by the movement of the puller. Mathematically, if the coordinates of the object are , the of the puller is y + \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Breather Surface
In differential geometry, a breather surface is a one-parameter family of mathematical surfaces which correspond to breather solutions of the sine-Gordon equation, a differential equation appearing in theoretical physics. The surfaces have the remarkable property that they have constant curvature -1, where the curvature is well-defined. This makes them examples of generalized pseudospheres. Mathematical background There is a correspondence between embedded surfaces of constant curvature -1, known as pseudospheres, and solutions to the sine-Gordon equation. This correspondence can be built starting with the simplest example of a pseudosphere, the tractroid. In a special set of coordinates, known as asymptotic coordinates, the Gauss–Codazzi equations, which are consistency equations dictating when a surface of prescribed first and second fundamental form can be embedded into three-dimensional space with the flat metric, reduce to the sine-Gordon equation. In the corresponde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |