|
Digital Down Converter
In digital signal processing, a digital down-converter (DDC) converts a digitized, band-limited signal to a lower frequency signal at a lower sampling rate in order to simplify the subsequent radio stages. The process can preserve all the information in the frequency band of interest of the original signal. The input and output signals can be real or complex samples. Often the DDC converts from the raw radio frequency or intermediate frequency down to a complex baseband signal. Architecture A DDC consists of three subcomponents: a direct digital synthesizer (DDS), a low-pass filter (LPF), and a downsampler (which may be integrated into the low-pass filter). The DDS generates a complex sinusoid at the intermediate frequency (IF). Multiplication of the intermediate frequency with the input signal creates images centered at the sum and difference frequency (which follows from the frequency shifting properties of the Fourier transform). The lowpass filters pass the difference (i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Digital Signal Processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor. Digital signal processing and analog signal processing are subfields of signal processing. DSP applications include audio and speech processing, sonar, radar and other sensor array processing, spectral density estimation, statistical signal processing, digital image processing, data compression, video coding, audio coding, image compression, signal processing for telecommunications, control systems, biomedical engineering, and seismology, among others. DSP can involve linear or nonli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
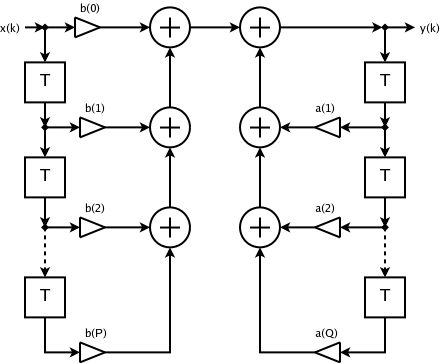
Infinite Impulse Response
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response h(t) which does not become exactly zero past a certain point, but continues indefinitely. This is in contrast to a finite impulse response (FIR) system in which the impulse response ''does'' become exactly zero at times t>T for some finite T, thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as ''IIR systems'' or ''IIR filters''. In practice, the impulse response, even of IIR systems, usually approaches zero and can be neglected past a certain point. However the physical systems which give rise to IIR or FIR responses are dissimilar, and therein lies the importance of the distinction. For instance, analog electronic filters composed of resistors, capacitors, and/or inductors (and perhaps linear amplifiers) are generally IIR filter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CORDIC
CORDIC (for "coordinate rotation digital computer"), also known as Volder's algorithm, or: Digit-by-digit method Circular CORDIC (Jack E. Volder), Linear CORDIC, Hyperbolic CORDIC (John Stephen Walther), and Generalized Hyperbolic CORDIC (GH CORDIC) (Yuanyong Luo et al.), is a simple and efficient algorithm to calculate trigonometric functions, hyperbolic functions, square roots, multiplications, divisions, and exponentials and logarithms with arbitrary base, typically converging with one digit (or bit) per iteration. CORDIC is therefore also an example of digit-by-digit algorithms. CORDIC and closely related methods known as pseudo-multiplication and pseudo-division or factor combining are commonly used when no hardware multiplier is available (e.g. in simple microcontrollers and FPGAs), as the only operations it requires are additions, subtractions, bitshift and lookup tables. As such, they all belong to the class of shift-and-add algorithms. In computer science, CORDIC is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analog-to-digital Converter
In electronics, an analog-to-digital converter (ADC, A/D, or A-to-D) is a system that converts an analog signal, such as a sound picked up by a microphone or light entering a digital camera, into a digital signal. An ADC may also provide an isolated measurement such as an electronic device that converts an analog input voltage or current to a digital number representing the magnitude of the voltage or current. Typically the digital output is a two's complement binary number that is proportional to the input, but there are other possibilities. There are several ADC architectures. Due to the complexity and the need for precisely matched components, all but the most specialized ADCs are implemented as integrated circuits (ICs). These typically take the form of metal–oxide–semiconductor (MOS) mixed-signal integrated circuit chips that integrate both analog and digital circuits. A digital-to-analog converter (DAC) performs the reverse function; it converts a digital signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Application-specific Integrated Circuit
An application-specific integrated circuit (ASIC ) is an integrated circuit (IC) chip customized for a particular use, rather than intended for general-purpose use, such as a chip designed to run in a digital voice recorder or a high-efficiency video codec. Application-specific standard product (ASSP) chips are intermediate between ASICs and industry standard integrated circuits like the 7400 series or the 4000 series. ASIC chips are typically fabricated using metal-oxide-semiconductor (MOS) technology, as MOS integrated circuit chips. As feature sizes have shrunk and design tools improved over the years, the maximum complexity (and hence functionality) possible in an ASIC has grown from 5,000 logic gates to over 100 million. Modern ASICs often include entire microprocessors, memory blocks including ROM, RAM, EEPROM, flash memory and other large building blocks. Such an ASIC is often termed a SoC (system-on-chip). Designers of digital ASICs often use a hardware descrip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field-programmable Gate Array
A field-programmable gate array (FPGA) is an integrated circuit designed to be configured by a customer or a designer after manufacturinghence the term '' field-programmable''. The FPGA configuration is generally specified using a hardware description language (HDL), similar to that used for an application-specific integrated circuit (ASIC). Circuit diagrams were previously used to specify the configuration, but this is increasingly rare due to the advent of electronic design automation tools. FPGAs contain an array of programmable logic blocks, and a hierarchy of reconfigurable interconnects allowing blocks to be wired together. Logic blocks can be configured to perform complex combinational functions, or act as simple logic gates like AND and XOR. In most FPGAs, logic blocks also include memory elements, which may be simple flip-flops or more complete blocks of memory. Many FPGAs can be reprogrammed to implement different logic functions, allowing flexible reconfigur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Costas Loop
A Costas loop is a phase-locked loop (PLL) based circuit which is used for carrier frequency recovery from suppressed-carrier modulation signals (e.g. double-sideband suppressed carrier signals) and phase modulation signals (e.g. BPSK, QPSK). It was invented by John P. Costas at General Electric in the 1950s. Its invention was described as having had "a profound effect on modern digital communications". The primary application of Costas loops is in wireless receivers. Its advantage over other PLL-based detectors is that at small deviations the Costas loop error voltage is \sin(2(\theta_i-\theta_f)) as compared to \sin(\theta_i-\theta_f). This translates to double the sensitivity and also makes the Costas loop uniquely suited for tracking Doppler-shifted carriers, especially in OFDM and GPS receivers. Classical implementation In the classical implementation of a Costas loop, a local voltage-controlled oscillator (VCO) provides quadrature outputs, one to each of two phase dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase-shift Keying
Phase-shift keying (PSK) is a digital modulation process which conveys data by changing (modulating) the phase of a constant frequency reference signal (the carrier wave). The modulation is accomplished by varying the sine and cosine inputs at a precise time. It is widely used for wireless LANs, RFID and Bluetooth communication. Any digital modulation scheme uses a finite number of distinct signals to represent digital data. PSK uses a finite number of phases, each assigned a unique pattern of binary digits. Usually, each phase encodes an equal number of bits. Each pattern of bits forms the symbol that is represented by the particular phase. The demodulator, which is designed specifically for the symbol-set used by the modulator, determines the phase of the received signal and maps it back to the symbol it represents, thus recovering the original data. This requires the receiver to be able to compare the phase of the received signal to a reference signal such a system is termed c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Locked Loop
A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is related to the phase of an input signal. There are several different types; the simplest is an electronic circuit consisting of a variable frequency oscillator and a phase detector in a feedback loop. The oscillator's frequency and phase are controlled proportionally by an applied voltage, hence the term voltage-controlled oscillator (VCO). The oscillator generates a periodic signal of a specific frequency, and the phase detector compares the phase of that signal with the phase of the input periodic signal, to adjust the oscillator to keep the phases matched. Keeping the input and output phase in lockstep also implies keeping the input and output frequencies the same. Consequently, in addition to synchronizing signals, a phase-locked loop can track an input frequency, or it can generate a frequency that is a multiple of the input frequency. These properties are use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carrier Recovery
A carrier recovery system is a circuit used to estimate and compensate for frequency and phase differences between a received signal's carrier wave and the receiver's local oscillator for the purpose of coherent demodulation. In the transmitter of a communications carrier system, a carrier wave is modulated by a baseband signal. At the receiver, the baseband information is extracted from the incoming modulated waveform. In an ideal communications system, the carrier signal oscillators of the transmitter and receiver would be perfectly matched in frequency and phase, thereby permitting perfect coherent demodulation of the modulated baseband signal. However, transmitters and receivers rarely share the same carrier oscillator. Communications receiver systems are usually independent of transmitting systems and contain their oscillators with frequency and phase offsets and instabilities. Doppler shift may also contribute to frequency differences in mobile radio frequency communicatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the output signa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |