|
Development (differential Geometry)
Development or developing may refer to: Arts *Development (music), the process by which thematic material is reshaped * Photographic development *Filmmaking, development phase, including finance and budgeting * Development hell, when a project is stuck in development * Development (band), English progressive pop rock band * ''Development'' (album), a 2002 album by Nonpoint Business * Business development, a process of growing a business *Career development * Corporate development, a position in a business * Energy development, activities concentrated on obtaining energy from natural resources *Green development, a real estate concept that considers social and environmental impact of development * Land development, altering the landscape in any number of ways * Land development bank, a kind of bank in India * Leadership development * New product development * Organization development *Professional development *Real estate development *Research and development * Training and de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Development (music)
In music, development is a process by which a musical idea is Transformation (music), transformed and Theme (music), restated in the course of a Musical piece, composition. Certain central ideas are repeated in different contexts or in altered form so that the listener can consciously or unconsciously compare the various statements of the idea, often in surprising or irony, ironic manners. This practice has its roots in counterpoint, where a theme or subject might create an impression of a pleasing or affective sort, but delight the mind further as its contrapuntal capabilities are gradually unveiled. Development is often contrasted with musical Variation (music), variation, which is a slightly different means to the same end. Development is carried out upon portions of material treated in ''many'' different presentations and combinations at a time, while variation depends upon ''one'' type of presentation at a time. The development is the middle section of the sonata form, betw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Estate Development
Real estate development, or property development, is a business process, encompassing activities that range from the renovation and re-lease of existing buildings to the purchase of raw Real Estate, land and the sale of developed land or parcels to others. Real estate developers are the people and companies who coordinate all of these activities, converting ideas from paper to real property. Real estate development is different from construction or Home construction, housebuilding, although many developers also manage the construction process or engage in housebuilding. Developers buy land, finance real estate deals, build or have builders build projects, develop projects in joint ventures, and create, imagine, control, and orchestrate the process of development from beginning to end.New York Times, March 16, 1963, "Personality Boom is Loud for Louis Lesser" Developers usually take the greatest risk in the creation or renovation of real estate and receive the greatest rewards. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Personal Development
Personal development or self-improvement consists of activities that develops a person's capabilities and potential, enhance quality of life, and facilitate the realization of dreams and aspirations. Personal development may take place over the course of an individual's entire lifespan and is not limited to one stage of a person's life. It can include official and informal actions for developing others in roles such as a teacher, guide, counselor, manager, coach, or mentor, and it is not restricted to self-help. When personal development takes place in the context of institutions, it refers to the methods, programs, tools, techniques, and assessment systems offered to support positive adult development at the individual level in organizations. Overview Among other things, personal development may include the following activities: * Social entrepreneurship or civic engagement * Participating in festivals, conferences, or conventions * Improving self-awareness * Improvin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neural Development
The development of the nervous system, or neural development (neurodevelopment), refers to the processes that generate, shape, and reshape the nervous system of animals, from the earliest stages of embryonic development to adulthood. The field of neural development draws on both neuroscience and developmental biology to describe and provide insight into the cellular and molecular mechanisms by which complex nervous systems develop, from nematodes and Drosophila melanogaster, fruit flies to mammals. Defects in neural development can lead to malformations such as holoprosencephaly, and a wide variety of neurological disorders including paresis, limb paresis and paralysis, balance and vision disorders, and seizures, and in humans other disorders such as Rett syndrome, Down syndrome and intellectual disability. Vertebrate brain development The vertebrate central nervous system (CNS) is derived from the ectoderm—the outermost germ layer of the embryo. A part of the dorsal ect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Human Development (biology)
Development of the human body is the process of growth to maturity. The process begins with fertilization, where an egg released from the ovary of a female is penetrated by a sperm cell from a male. The resulting zygote develops through mitosis and cell differentiation, and the resulting embryo then implants in the uterus, where the embryo continues development through a fetal stage until birth. Further growth and development continues after birth, and includes both physical and psychological development that is influenced by genetic, hormonal, environmental and other factors. This continues throughout life: through childhood and adolescence into adulthood. Before birth Development before birth, or prenatal development () is the process in which a zygote, and later an embryo, and then a fetus develops during gestation. Prenatal development starts with fertilization and the formation of the zygote, the first stage in embryonic development which continues in fetal de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Embryogenesis
An embryo ( ) is the initial stage of development for a multicellular organism. In organisms that reproduce sexually, embryonic development is the part of the life cycle that begins just after fertilization of the female egg cell by the male sperm cell. The resulting fusion of these two cells produces a single-celled zygote that undergoes many cell divisions that produce cells known as blastomeres. The blastomeres (4-cell stage) are arranged as a solid ball that when reaching a certain size, called a morula, (16-cell stage) takes in fluid to create a cavity called a blastocoel. The structure is then termed a blastula, or a blastocyst in mammals. The mammalian blastocyst hatches before implantating into the endometrial lining of the womb. Once implanted the embryo will continue its development through the next stages of gastrulation, neurulation, and organogenesis. Gastrulation is the formation of the three germ layers that will form all of the different parts o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
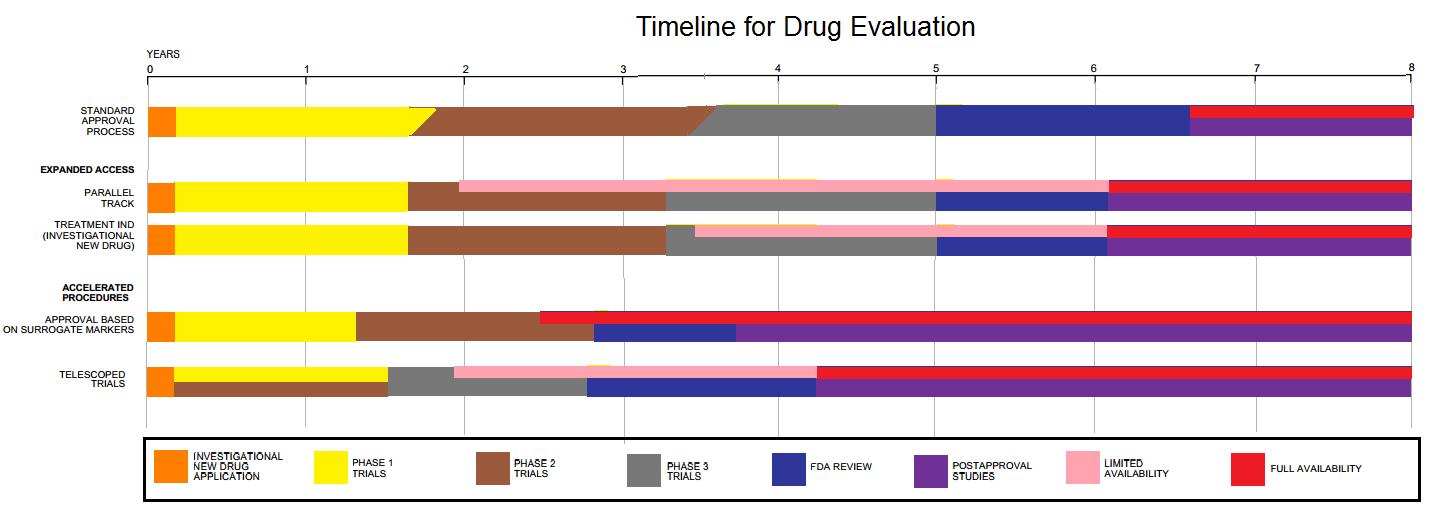
Drug Development
Drug development is the process of bringing a new pharmaceutical drug to the market once a lead compound has been identified through the process of drug discovery. It includes preclinical research on microorganisms and animals, filing for regulatory status, such as via the United States Food and Drug Administration for an investigational new drug to initiate clinical trials on humans, and may include the step of obtaining regulatory approval with a new drug application to market the drug. The entire process—from concept through preclinical testing in the laboratory to clinical trial development, including Phase I–III trials—to approved vaccine or drug typically takes more than a decade. New chemical entity development Broadly, the process of drug development can be divided into preclinical and clinical work. Pre-clinical New chemical entities (NCEs, also known as new molecular entities or NMEs) are compounds that emerge from the process of drug discovery. These h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Developmental Psychology
Developmental psychology is the scientific study of how and why humans grow, change, and adapt across the course of their lives. Originally concerned with infants and children, the field has expanded to include adolescence, adult development, aging, and the entire lifespan. Developmental psychologists aim to explain how thinking, feeling, and behaviors change throughout life. This field examines change across three major dimensions, which are physical development, cognitive development, and social emotional development. Within these three dimensions are a broad range of topics including motor skills, executive functions, moral understanding, language acquisition, social change, personality, emotional development, self-concept, and identity formation. Developmental psychology examines the influences of nature ''and'' nurture on the process of human development, as well as processes of change in context across time. Many researchers are interested in the interactions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Developmental Biology
Developmental biology is the study of the process by which animals and plants grow and develop. Developmental biology also encompasses the biology of Regeneration (biology), regeneration, asexual reproduction, metamorphosis, and the growth and differentiation of stem cells in the adult organism. Perspectives The main processes involved in the embryogenesis, embryonic development of animals are: tissue patterning (via regional specification and patterned cellular differentiation, cell differentiation); tissue growth; and tissue morphogenesis. * Regional specification refers to the processes that create the spatial patterns in a ball or sheet of initially similar cells. This generally involves the action of cytoplasmic determinants, located within parts of the fertilized egg, and of inductive signals emitted from signaling centers in the embryo. The early stages of regional specification do not generate functional differentiated cells, but cell populations committed to developing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Development (journal)
''Development'' is a bi-weekly peer-reviewed scientific journal in the field of developmental biology that covers cellular and molecular mechanisms of animal and plant development. It is published by The Company of Biologists. ''Development'' is partnered with Publons, is part of the Review Commons initiative and has two-way integration with bioRxiv. In 2009, the BioMedical & Life Sciences Division of the Special Libraries Association included ''Development'' in their list of top 100 journals in Biology and Medicine over the last 100 years. Brief history Originally called ''Journal of Embryology and Experimental Morphology'' () and established in 1953, the journal provided a periodical that would be primarily devoted to morphogenesis. In 1987, the journal was renamed ''Development''. The journal's full archive from 1953 is available online. ''Development'' is now a hybrid journal and publishes 24 issues a year. Content over 6 months old is free to read. Scope and content ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Child Development
Child development involves the Human development (biology), biological, psychological and emotional changes that occur in human beings between birth and the conclusion of adolescence. It is—particularly from birth to five years— a foundation for a prosperous and sustainable society.Center on the Developing Child (2007). The Science of Early Childhood Development (InBrief). Retrieved from www.developingchild.harvard.edu. Childhood is divided into three stages of life which include early childhood, middle childhood, and late childhood (preadolescence). Early childhood typically ranges from infancy to the age of 6 years old. Early childhood development, During this period, development is significant, as many of life's milestones happen during this time period such as first words, learning to crawl, and learning to walk. Middle childhood/preadolescence or ages 6–12 universally mark a distinctive period between major developmental transition points. Adolescence is the stage of l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adult Development
Adult development encompasses the changes that occur in biological and psychological domains of human life from the end of adolescence until the end of one's life. Changes occur at the cellular level and are partially explained by biological theories of adult development and aging. Biological changes influence psychological and interpersonal/social developmental changes, which are often described by stage theories of human development. Stage theories typically focus on "age-appropriate" developmental tasks to be achieved at each stage. Erik Erikson and Carl Jung proposed stage theories of human development that encompass the entire life span, and emphasized the potential for positive change very late in life. The concept of adulthood has legal and socio-cultural definitions. The legal definition of an adult is a person who is fully grown or developed. This is referred to as the age of majority, which is age 18 in most cultures, although there is a variation from 15 to 21. The ty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |