|
Descendant Tree (group Theory)
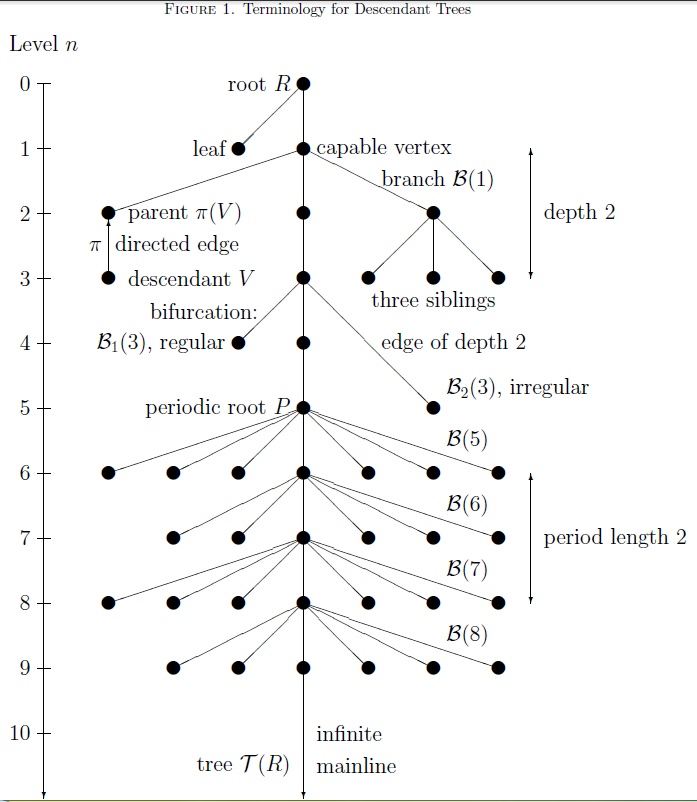
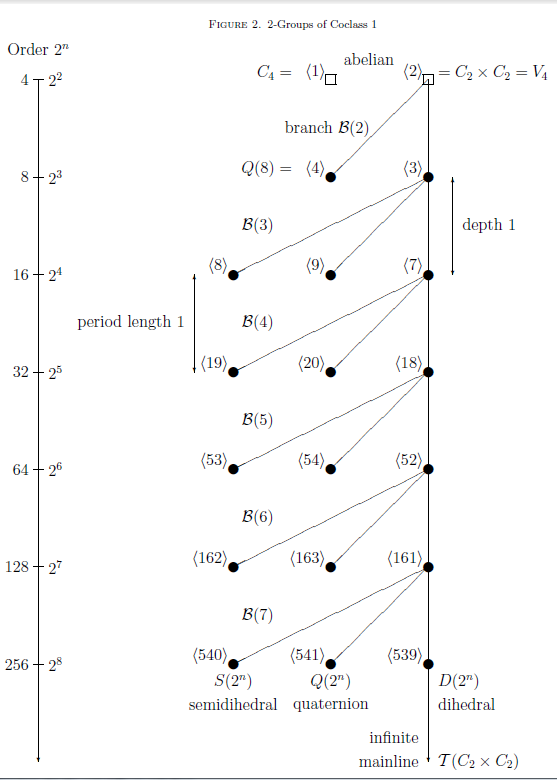
In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order p^n, for a fixed prime number p and varying integer exponents n\ge 0. Such groups are briefly called ''finite'' ''p-groups''. The ''vertices'' of a descendant tree are isomorphism classes of finite ''p''-groups. Additionally to their ''order'' p^n, finite ''p''-groups have two further related invariants, the ''nilpotency class'' c and the coclass r=n-c. It turned out that descendant trees of a particular kind, the so-called pruned coclass trees whose infinitely many vertices share a common coclass r, reveal a repeating finite pattern. These two crucial properties of finiteness and periodicity admit a characterization of all members of the tree by finitely many parametrized presentations. Consequently, descendant trees play a fundamental role in the classification of finite ''p''-groups ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group Theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field (mathematics), fields, and vector spaces, can all be seen as groups endowed with additional operation (mathematics), operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, and Standard Model, three of the four known fundamental forces in the universe, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pro-p Group
In mathematics, a pro-''p'' group (for some prime number ''p'') is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a ''p''-group. Note that, as profinite groups are compact, the open subgroups are exactly the closed subgroups of finite index, so that the discrete quotient group is always finite. Alternatively, one can define a pro-''p'' group to be the inverse limit of an inverse system of discrete finite ''p''-groups. The best-understood (and historically most important) class of pro-''p'' groups is the ''p''-adic analytic groups: groups with the structure of an analytic manifold over \mathbb_p such that group multiplication and inversion are both analytic functions. The work of Lubotzky and Mann, combined with Michel Lazard's solution to Hilbert's fifth problem over the ''p''-adic numbers, shows that a pro-''p'' group is ''p''-adic analytic if and only if it has finite rank, i.e. there exists a positive integer r suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giuseppe Bagnera (mathematician)
Giuseppe Bagnera (14 November 1865 – 12 May 1927) was an Italian mathematician. Biography At the University of Palermo, Bagnera received his ''laurea'' in civil engineering in 1890 and then his ''laurea'' in mathematics in 1895. His teachers included Giovanni Battista Guccia, Francesco Gerbaldi ed Ernesto Cesàro. In 1899 he was appointed ''libero docente'' (lecturer) in algebraic analysis at the University of Palermo. He was appointed professor extraordinarius of infinitesimal calculus in 1901, then professor ordinarius in 1905, at the University of Messina, where he remained until the 1908 earthquake. He then taught at the University of Palermo until 1922 when he moved to the Sapienza University of Rome, where he taught until his death.Bagnera, Giuseppi — Treccani, Dizi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descendant Tree (group Theory)
In mathematics, specifically group theory, a descendant tree is a hierarchical structure that visualizes parent-descendant relations between isomorphism classes of finite groups of prime power order p^n, for a fixed prime number p and varying integer exponents n\ge 0. Such groups are briefly called ''finite'' ''p-groups''. The ''vertices'' of a descendant tree are isomorphism classes of finite ''p''-groups. Additionally to their ''order'' p^n, finite ''p''-groups have two further related invariants, the ''nilpotency class'' c and the coclass r=n-c. It turned out that descendant trees of a particular kind, the so-called pruned coclass trees whose infinitely many vertices share a common coclass r, reveal a repeating finite pattern. These two crucial properties of finiteness and periodicity admit a characterization of all members of the tree by finitely many parametrized presentations. Consequently, descendant trees play a fundamental role in the classification of finite ''p''-groups ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cohomology
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups, usually one associated with a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory. From its beginning in topology, this idea became a dominant method in the mathematics of the second half of the twentieth century. From the initial idea of homology as a method of constructing algebraic invariants of topological spaces, the range of applications of homology and cohomology theories has spread throughout geometry and algebra. The terminology tends to hide the fact that cohomology, a contravariant theory, is more natural than homology in many applications. At a basic level, this has to do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in education, to the study of algebraic structures such as groups, rings, and fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, some having "algebra" in their name, such as commutative algebra, and some not, such as Galois theory. The word ''algebra'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
