|
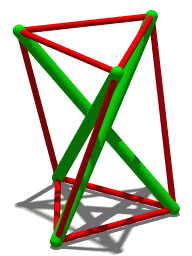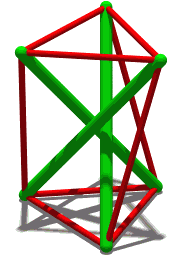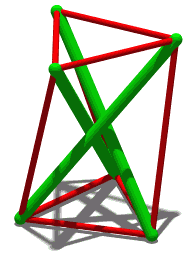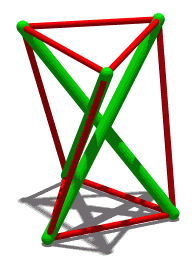
Counting On Frameworks
''Counting on Frameworks: Mathematics to Aid the Design of Rigid Structures'' is an undergraduate-level book on the mathematics of structural rigidity. It was written by Jack E. Graver and published in 2001 by the Mathematical Association of America as volume 25 of the Dolciani Mathematical Expositions book series. The Basic Library List Committee of the Mathematical Association of America has recommended its inclusion by undergraduate mathematics libraries. Topics The problems considered by ''Counting on Frameworks'' primarily concern systems of rigid rods, connected to each other by flexible joints at their ends; the question is whether these connections fix such a framework into a single position, or whether it can flex continuously through multiple positions. Variations of this problem include the simplest way to add rods to a framework to make it rigid, or the resilience of a framework against the failure of one of its rods. To study this question, Graver has organized ''Coun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Rigidity
In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges. Definitions Rigidity is the property of a structure that it does not bend or flex under an applied force. The opposite of rigidity is flexibility. In structural rigidity theory, structures are formed by collections of objects that are themselves rigid bodies, often assumed to take simple geometric forms such as straight rods (line segments), with pairs of objects connected by flexible hinges. A structure is rigid if it cannot flex; that is, if there is no continuous motion of the structure that preserves the shape of its rigid components and the pattern of their connections at the hinges. There are two essentially different kinds of rigidity. Finite or macroscopic rigidity means that the structure will not flex, fold, or bend by a positive amount. Infinitesimal rigidity means that the st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic Dome
A geodesic dome is a hemispherical thin-shell structure (lattice-shell) based on a geodesic polyhedron. The triangular elements of the dome are structurally rigid and distribute the structural stress throughout the structure, making geodesic domes able to withstand very heavy loads for their size. History The first geodesic dome was designed after World War I by Walther Bauersfeld, chief engineer of the Carl Zeiss optical company, for a planetarium to house his planetarium projector. An initial, small dome was patented and constructed by the firm of Dykerhoff and Wydmann on the roof of the Zeiss plant in Jena, Germany. A larger dome, called "The Wonder of Jena", opened to the public in July 1926. Twenty years later, Buckminster Fuller coined the term "geodesic" from field experiments with artist Kenneth Snelson at Black Mountain College in 1948 and 1949. Although Fuller was not the original inventor, he is credited with the U.S. popularization of the idea for which he rece ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Books
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MathSciNet
MathSciNet is a searchable online bibliographic database created by the American Mathematical Society in 1996. It contains all of the contents of the journal ''Mathematical Reviews'' (MR) since 1940 along with an extensive author database, links to other MR entries, citations, full journal entries, and links to original articles. It contains almost 3.6 million items and over 2.3 million links to original articles. Along with its parent publication ''Mathematical Reviews'', MathSciNet has become an essential tool for researchers in the mathematical sciences. Access to the database is by subscription only and is not generally available to individual researchers who are not affiliated with a larger subscribing institution. For the first 40 years of its existence, traditional typesetting was used to produce the Mathematical Reviews journal. Starting in 1980 bibliographic information and the reviews themselves were produced in both print and electronic form. This formed the basis of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ZbMATH
zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure mathematics, pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastructure GmbH. Editors are the European Mathematical Society, FIZ Karlsruhe, and the Heidelberg Academy of Sciences. zbMATH is distributed by Springer Science+Business Media. It uses the Mathematics Subject Classification codes for organising reviews by topic. History Mathematicians Richard Courant, Otto Neugebauer, and Harald Bohr, together with the publisher Ferdinand Springer, took the initiative for a new mathematical reviewing journal. Harald Bohr worked in Copenhagen. Courant and Neugebauer were professors at the University of Göttingen. At that time, Göttingen was considered one of the central places for mathematical research, having appointed mathematicians like David Hilbert, Hermann Minkowski, Carl Runge, and Felix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Mathematics Teacher
Founded in 1920, The National Council of Teachers of Mathematics (NCTM) is a professional organization for schoolteachers of mathematics in the United States. One of its goals is to improve the standards of mathematics in education. NCTM holds annual national and regional conferences for teachers and publishes five journals. Journals NCTM publishes five official journals. All are available in print and online versions. ''Teaching Children Mathematics'' supports improvement of pre-K–6 mathematics education by serving as a resource for teachers so as to provide more and better mathematics for all students. It is a forum for the exchange of mathematics idea, activities, and pedagogical strategies, and or sharing and interpreting research. ''Mathematics Teaching in the Middle School'' supports the improvement of grade 5–9 mathematics education by serving as a resource for practicing and prospective teachers, as well as supervisors and teacher educators. It is a forum for the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematika
''Mathematika'' is a peer-reviewed mathematics journal that publishes both pure and applied mathematical articles. The journal was founded by Harold Davenport in the 1950s. The journal is published by the London Mathematical Society, on behalf of the journal's owner University College London. Indexing and abstracting According to the ''Journal Citation Reports'', the journal has a 2020 impact factor of 0.844. The journal in indexing in the following bibliographic databases: * MathSciNet * Science Citation Index Expanded * Web of Science * Zentralblatt MATH zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastructur ... References {{reflist London Mathematical Society Mathematics education in the United Kingdom Mathematics journals Publications established in 1954 Quarterly journals W ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariable Calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving several variables, rather than just one. Multivariable calculus may be thought of as an elementary part of advanced calculus. For advanced calculus, see calculus on Euclidean space. The special case of calculus in three dimensional space is often called vector calculus. Typical operations Limits and continuity A study of limits and continuity in multivariable calculus yields many counterintuitive results not demonstrated by single-variable functions. For example, there are scalar functions of two variables with points in their domain which give different limits when approached along different paths. E.g., the function. :f(x,y) = \frac approaches zero whenever the point (0,0) is approached along lines through the origin (y=kx). However, when the origin is appr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensegrity
Tensegrity, tensional integrity or floating compression is a structural principle based on a system of isolated components under compression inside a network of continuous tension, and arranged in such a way that the compressed members (usually bars or struts) do not touch each other while the prestressed tensioned members (usually cables or tendons) delineate the system spatially. The term was coined by Buckminster Fuller in the 1960s as a portmanteau of "tensional integrity". The other denomination of tensegrity, ''floating compression'', was used mainly by the constructivist artist Kenneth Snelson. Concept Tensegrity structures are based on the combination of a few simple design patterns: * members loaded in either pure compression or pure tension, which means that the structure will only fail if the cables yield or the rods buckle. This enables the material properties and cross-sectional geometry of each member to be optimized to the particular load it carries. * preload ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linkage (mechanical)
A mechanical linkage is an assembly of systems connected to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain. Linkages may be constructed from open chains, closed chains, or a combination of open and closed chains. Each link in a chain is connected by a joint to one or more other links. Thus, a kinematic chain can be modeled as a graph in which the links are paths and the joints are vertices, which is called a linkage graph. The movement of an ideal joint is generally associated with a subgroup of the group of Euclidean displacements. The number of parameters in the subgroup is called the degrees of freedom (DOF) of the joint. Mechanical linkages are usually designed to tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Association Of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university, college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists; statisticians; and many others in academia, government, business, and industry. The MAA was founded in 1915 and is headquartered at 1529 18th Street, Northwest in the Dupont Circle neighborhood of Washington, D.C. The organization publishes mathematics journals and books, including the '' American Mathematical Monthly'' (established in 1894 by Benjamin Finkel), the most widely read mathematics journal in the world according to records on JSTOR. Mission and Vision The mission of the MAA is to advance the understanding of mathematics and its impact on our world. We envision a society that values the power and beauty of mathematics and fully realizes its potential to promote human flourishing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. The two sets U and V may be thought of as a coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another red, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color. One often writes G=(U,V,E) to denote a bipartite graph whose partition has the parts U and V, with E denoting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


(y))⁄((x^4) (y^2)).png)
.jpg)