|
Continuous-time Random Walk
In mathematics, a continuous-time random walk (CTRW) is a generalization of a random walk where the wandering particle waits for a random time between jumps. It is a stochastic jump process with arbitrary distributions of jump lengths and waiting times. More generally it can be seen to be a special case of a Markov renewal process. Motivation CTRW was introduced by Montroll and Weiss as a generalization of physical diffusion process to effectively describe anomalous diffusion, i.e., the super- and sub-diffusive cases. An equivalent formulation of the CTRW is given by generalized master equations. A connection between CTRWs and diffusion equations with fractional time derivatives has been established. Similarly, time-space fractional diffusion equations can be considered as CTRWs with continuously distributed jumps or continuum approximations of CTRWs on lattices. Formulation A simple formulation of a CTRW is to consider the stochastic process X(t) defined by : X(t) = X_0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. In a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic
Stochastic (, ) refers to the property of being well described by a random probability distribution. Although stochasticity and randomness are distinct in that the former refers to a modeling approach and the latter refers to phenomena themselves, these two terms are often used synonymously. Furthermore, in probability theory, the formal concept of a ''stochastic process'' is also referred to as a ''random process''. Stochasticity is used in many different fields, including the natural sciences such as biology, chemistry, ecology, neuroscience, and physics, as well as technology and engineering fields such as image processing, signal processing, information theory, computer science, cryptography, and telecommunications. It is also used in finance, due to seemingly random changes in financial markets as well as in medicine, linguistics, music, media, colour theory, botany, manufacturing, and geomorphology. Etymology The word ''stochastic'' in English was originally used as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jump Process
A jump process is a type of stochastic process that has discrete movements, called jumps, with random arrival times, rather than continuous movement, typically modelled as a simple or compound Poisson process. In finance, various stochastic models are used to model the price movements of financial instruments; for example the Black–Scholes model for pricing options assumes that the underlying instrument follows a traditional diffusion process, with continuous, random movements at all scales, no matter how small. John Carrington Cox and Stephen Ross proposed that prices actually follow a 'jump process'. Robert C. Merton extended this approach to a hybrid model known as jump diffusion, which states that the prices have large jumps interspersed with small continuous movements. See also *Poisson process, an example of a jump process *Continuous-time Markov chain (CTMC), an example of a jump process and a generalization of the Poisson process *Counting process, an example of a j ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Renewal Process
In probability and statistics, a Markov renewal process (MRP) is a random process that generalizes the notion of Markov jump processes. Other random processes like Markov chains, Poisson processes and renewal processes can be derived as special cases of MRP's. Definition Consider a state space \mathrm. Consider a set of random variables (X_n,T_n), where T_n are the jump times and X_n are the associated states in the Markov chain (see Figure). Let the inter-arrival time, \tau_n=T_n-T_. Then the sequence (X_n,T_n) is called a Markov renewal process if : \begin & \Pr(\tau_\le t, X_=j\mid(X_0, T_0), (X_1, T_1),\ldots, (X_n=i, T_n)) \\ pt= & \Pr(\tau_\le t, X_=j\mid X_n=i)\, \forall n \ge1,t\ge0, i,j \in \mathrm \end Relation to other stochastic processes # If we define a new stochastic process Y_t:=X_n for t \in _n,T_), then the process Y_t is called a semi-Markov process. Note the main difference between an MRP and a semi-Markov process is that the former is defined as a two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elliott Waters Montroll
Elliott Waters Montroll (May 4, 1916 in Pittsburgh, Pennsylvania, United States – December 3, 1983 in Chevy Chase, Maryland, United States) was an American scientist and mathematician. Education Elliott Montroll was born on May 4, 1916 in Pittsburgh, Pennsylvania, and received his elementary and high school education at the Dormont Public Schools. In 1933 he entered the University of Pittsburgh and in 1937 he received a BS degree in Chemistry. From 1937 until 1939 he was a graduate assistant in the Mathematics Department of the University of Pittsburgh, and during the first semester of the school year 1939–1940 he carried out research in the Chemistry Department of Columbia University. He was awarded a Ph.D in mathematics at the University of Pittsburgh in 1939, with a thesis ''Some Notes and Applications of the Characteristic Value Theory of Integral Equations'' in which he applied integral equations to the study of imperfect gases. A paper published jointly with Joseph E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Herbert Weiss
George H. Weiss (February 19, 1930 – February 14, 2017) was an American applied mathematician and physicist at the National Institutes of Health, known for his work on random walks. He did his undergraduate studies at the City College of New York and Columbia University, graduating in 1951, and earned a Ph.D. from the University of Maryland in 1958. Awards In 1967, Weiss and Marvin Zelen shared the Washington Academy of Sciences award for their contributions in Mathematics. Established in 1939, this award recognizes noteworthy accomplishments by young scientists (40 years of age and under). In May 2010, the NIH held a symposium entitled "Random Walks in Biology and Beyond", in honor of Weiss's 80th birthday and recent retirement. In July 2010, at the Mexican Meeting on Mathematical and Experimental Physics, Weiss was awarded the Leopoldo García-Colín-Scherer Medal. This medal has been established in 2001 and awarded every three years to recognize outstanding internation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anomalous Diffusion
Anomalous diffusion is a diffusion process with a non-linear relationship between the mean squared displacement (MSD), \langle r^(\tau )\rangle , and time. This behavior is in stark contrast to Brownian motion, the typical diffusion process described by Einstein and Smoluchowski, where the MSD is linear in time (namely, \langle r^(\tau )\rangle =2dD\tau with ''d'' being the number of dimensions and ''D'' the diffusion coefficient). Examples of anomalous diffusion in nature have been observed in biology in the cell nucleus, plasma membrane and cytoplasm. Unlike typical diffusion, anomalous diffusion is described by a power law, \langle r^(\tau )\rangle =K_\alpha\tau^\alphawhere K_\alpha is the so-called generalized diffusion coefficient and \tau is the elapsed time. In Brownian motion, α = 1. If α > 1, the process is superdiffusive. Superdiffusion can be the result of active cellular transport processes or due to jumps with a heavy-tail distribution. If α < 1, the par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Master Equation
In physics, chemistry and related fields, master equations are used to describe the time evolution of a system that can be modelled as being in a probabilistic combination of states at any given time and the switching between states is determined by a transition rate matrix. The equations are a set of differential equations – over time – of the probabilities that the system occupies each of the different states. Introduction A master equation is a phenomenological set of first-order differential equations describing the time evolution of (usually) the probability of a system to occupy each one of a discrete set of states with regard to a continuous time variable ''t''. The most familiar form of a master equation is a matrix form: : \frac=\mathbf\vec, where \vec is a column vector (where element ''i'' represents state ''i''), and \mathbf is the matrix of connections. The way connections among states are made determines the dimension of the problem; it is either *a d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
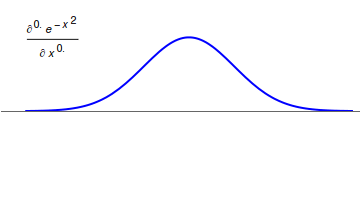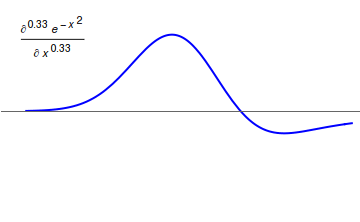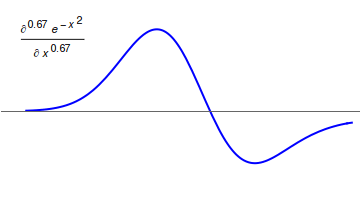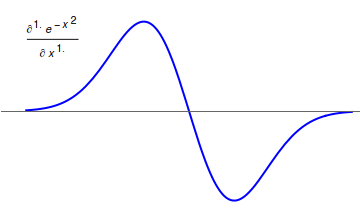
Fractional Derivative
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after its discoverer Pierre-Simon Laplace (), is an integral transform In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in ... that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex frequency domain, also known as ''s''-domain, or s-plane). The transform has many applications in science and engineering because it is a tool for solving differential equations. In particular, it transforms ordinary differential equations into algebraic equations and convolution into multiplication. For suitable functions ''f'', the Laplace transform is the integral \mathcal\(s) = \int_0^\infty f(t)e^ \, dt. H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Characteristic Function (probability Theory)
In probability theory and statistics, the characteristic function of any real-valued random variable completely defines its probability distribution. If a random variable admits a probability density function, then the characteristic function is the Fourier transform of the probability density function. Thus it provides an alternative route to analytical results compared with working directly with probability density functions or cumulative distribution functions. There are particularly simple results for the characteristic functions of distributions defined by the weighted sums of random variables. In addition to univariate distributions, characteristic functions can be defined for vector- or matrix-valued random variables, and can also be extended to more generic cases. The characteristic function always exists when treated as a function of a real-valued argument, unlike the moment-generating function. There are relations between the behavior of the characteristic function of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |