|
Compound Of Tesseract And 16-cell
In 4-dimensional geometry, the tesseract 16-cell compound is a polytope compound composed of a regular tesseract and its dual, the regular 16-cell. Its convex hull is the regular 24-cell, which is self-dual. A '' compound polytope'' is a figure that is composed of several polytopes sharing a common center. The outer vertices of a compound can be connected to form a convex polytope called its convex hull. The compound is a facetting of the convex hull. In 4-polytope compounds constructed as dual pairs, cells and vertices swap positions and faces and edges swap positions. Because of this the number of cells and vertices are equal, as are faces and edges. Mid-edges of the tesseract cross mid-face in the 16-cell, and vice versa. The tesseract 16-cell compound can be seen as the 4-dimensional analogue of a compound of cube and octahedron. It is one of four compound polytopes which are obtained by combining a regular convex 4-polytope with its dual; the other three being the compound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schläfli Symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations. The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more than three dimensions and discovered all their convex regular polytopes, including the six that occur in four dimensions. Definition The Schläfli symbol is a recursive description, starting with for a ''p''-sided regular polygon that is convex. For example, is an equilateral triangle, is a square, a convex regular pentagon, etc. Regular star polygons are not convex, and their Schläfli symbols contain irreducible fractions ''p''/''q'', where ''p'' is the number of vertices, and ''q'' is their turning number. Equivalently, is created from the vertices of , connected every ''q''. For example, is a pentagram; is a pentagon. A regular polyhedron that has ''q'' regular ''p''-sided polygon faces around each vertex is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Cube And Octahedron
The compound of cube and octahedron is a polyhedron which can be seen as either a polyhedral stellation or a compound. Construction The 14 Cartesian coordinates of the vertices of the compound are. : 6: (±2, 0, 0), ( 0, ±2, 0), ( 0, 0, ±2) : 8: ( ±1, ±1, ±1) As a compound It can be seen as the compound of an octahedron and a cube. It is one of four compounds constructed from a Platonic solid or Kepler-Poinsot polyhedron and its dual. It has octahedral symmetry (O''h'') and shares the same vertices as a rhombic dodecahedron. This can be seen as the three-dimensional equivalent of the compound of two squares ( " octagram"); this series continues on to infinity, with the four-dimensional equivalent being the compound of tesseract and 16-cell. As a stellation It is also the first stellation of the cuboctahedron and given as Wenninger model index 43. It can be seen as a cuboctahedron with square and triangular pyramids added to each face. The stellatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
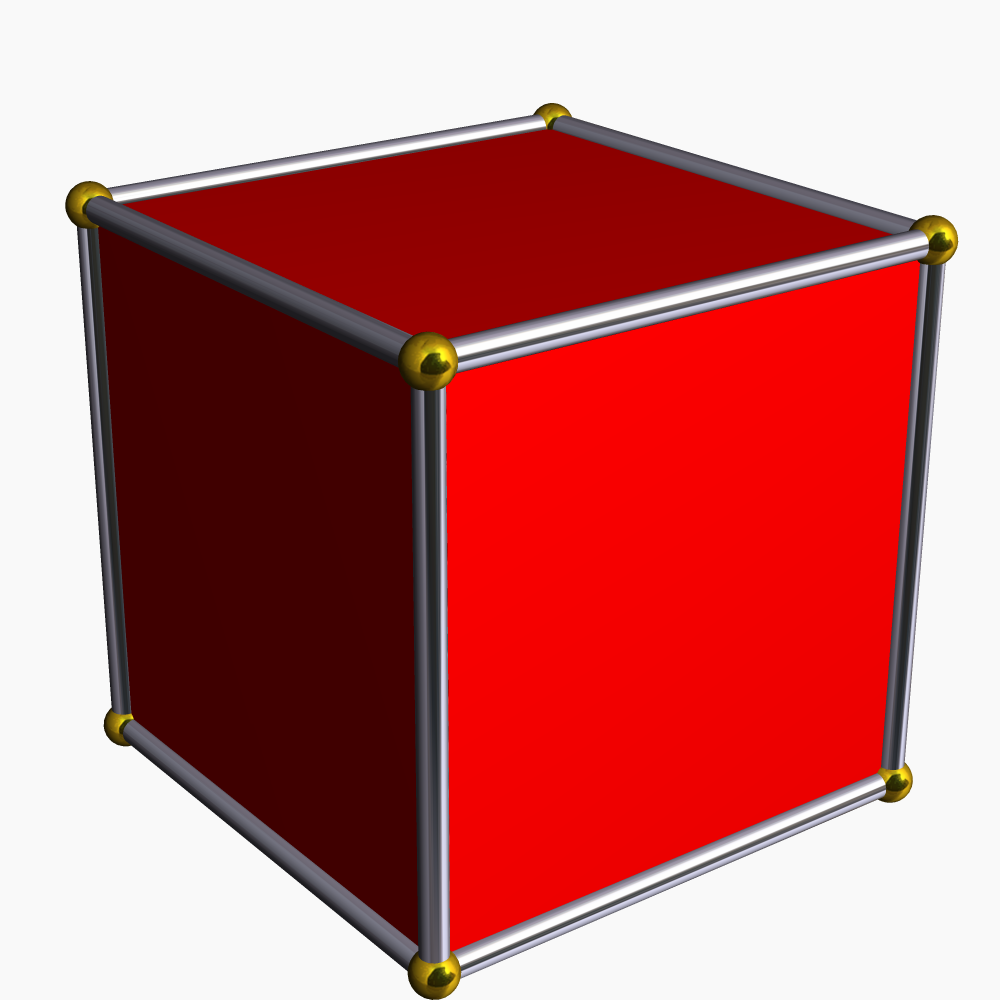
4-cube T12
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book ''A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-cube T3
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book ''A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
4-cube T0
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book ''A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coxeter Plane
In mathematics, the Coxeter number ''h'' is the order of a Coxeter element of an irreducible Coxeter group. It is named after H.S.M. Coxeter. Definitions Note that this article assumes a finite Coxeter group. For infinite Coxeter groups, there are multiple conjugacy classes of Coxeter elements, and they have infinite order. There are many different ways to define the Coxeter number ''h'' of an irreducible root system. A Coxeter element is a product of all simple reflections. The product depends on the order in which they are taken, but different orderings produce conjugate elements, which have the same order. *The Coxeter number is the order of any Coxeter element;. *The Coxeter number is 2''m''/''n'', where ''n'' is the rank, and ''m'' is the number of reflections. In the crystallographic case, ''m'' is half the number of roots; and ''2m''+''n'' is the dimension of the corresponding semisimple Lie algebra. *If the highest root is Σ''m''iα''i'' for simple roots α''i'', then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F4 (mathematics)
In mathematics, F4 is the name of a Lie group and also its Lie algebra f4. It is one of the five exceptional simple Lie groups. F4 has rank 4 and dimension 52. The compact form is simply connected and its outer automorphism group is the trivial group. Its fundamental representation is 26-dimensional. The compact real form of F4 is the isometry group of a 16-dimensional Riemannian manifold known as the octonionic projective plane OP2. This can be seen systematically using a construction known as the ''magic square'', due to Hans Freudenthal and Jacques Tits. There are 3 real forms: a compact one, a split one, and a third one. They are the isometry groups of the three real Albert algebras. The F4 Lie algebra may be constructed by adding 16 generators transforming as a spinor to the 36-dimensional Lie algebra so(9), in analogy with the construction of E8. In older books and papers, F4 is sometimes denoted by E4. Algebra Dynkin diagram The Dynkin diagram for F4 is: . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faceting
Stella octangula as a faceting of the cube In geometry, faceting (also spelled facetting) is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices. New edges of a faceted polyhedron may be created along face diagonals or internal space diagonals. A ''faceted polyhedron'' will have two faces on each edge and creates new polyhedra or compounds of polyhedra. Faceting is the reciprocal or dual process to '' stellation''. For every stellation of some convex polytope, there exists a dual faceting of the dual polytope. Faceted polygons For example, a regular pentagon has one symmetry faceting, the pentagram, and the regular hexagon has two symmetric facetings, one as a polygon, and one as a compound of two triangles. Faceted polyhedra The regular icosahedron can be faceted into three regular Kepler–Poinsot polyhedra: small stellated dodecahedron, great dodecahedron, and great icosahedron. They all have 30 edges. The reg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stellation
In geometry, stellation is the process of extending a polygon in two dimensions, polyhedron in three dimensions, or, in general, a polytope in ''n'' dimensions to form a new figure. Starting with an original figure, the process extends specific elements such as its edges or face planes, usually in a symmetrical way, until they meet each other again to form the closed boundary of a new figure. The new figure is a stellation of the original. The word ''stellation'' comes from the Latin ''stellātus'', "starred", which in turn comes from Latin ''stella'', "star". Stellation is the reciprocal or dual process to '' faceting''. Kepler's definition In 1619 Kepler defined stellation for polygons and polyhedra as the process of extending edges or faces until they meet to form a new polygon or polyhedron. He stellated the regular dodecahedron to obtain two regular star polyhedra, the small stellated dodecahedron and great stellated dodecahedron. He also stellated the regular octahe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |