|
Cohesion (structural)
In sociology, structural cohesion is the conception of a useful formal definition and measure of cohesion in social groups. It is defined as the minimal number of actors in a social network that need to be removed to disconnect the group. It is thus identical to the question of the node connectivity of a given graph in discrete mathematics. The vertex-cut version of Menger's theorem also proves that the disconnection number is equivalent to a maximally sized group with a network in which every pair of persons has at least this number of separate paths between them. It is also useful to know that -cohesive graphs (or -components) are always a subgraph of a -core, although a -core is not always -cohesive. A -core is simply a subgraph in which all nodes have at least neighbors but it need not even be connected. The boundaries of structural endogamy in a kinship group are a special case of structural cohesion. Software Cohesive.blockingis the R program for computing structural c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sociology
Sociology is a social science that focuses on society, human social behavior, patterns of Interpersonal ties, social relationships, social interaction, and aspects of culture associated with everyday life. It uses various methods of Empirical research, empirical investigation and critical analysis to develop a body of knowledge about social order and social change. While some sociologists conduct research that may be applied directly to social policy and welfare, others focus primarily on refining the Theory, theoretical understanding of social processes and phenomenology (sociology), phenomenological method. Subject matter can range from Microsociology, micro-level analyses of society (i.e. of individual interaction and agency (sociology), agency) to Macrosociology, macro-level analyses (i.e. of social systems and social structure). Traditional focuses of sociology include social stratification, social class, social mobility, sociology of religion, religion, secularization, S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Structural Endogamy
''Structural endogamy'' is a network concept that provides a means of finding the boundaries of endogamy in a community, using simply the genealogical and marriage linkages. The concept is related to that of structural cohesion. The examples are made with free tool Pajek. Another name for structural endogamy is (marital) relinking, which comes out of French social anthropology, and the study of how communities are formed through couples marrying who are already linked: linked, that is, by chains of kinship and marriage, as in circles of intermarrying families, or marriages between people with one or more ancestors in common (i.e., ''blood'' relatives, such as cousins). Many of the marriages represented in the Turkish nomads figure are with cousins, for example. But relinking also occurs without blood marriages, as in the example from the Mexican village of Belén Atzitzi-mititlán within Apetatitlán de Antonio Carvajal. References Structural endogamy and the Graphe de Paren ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Connectivity
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network. Connected vertices and graphs In an undirected graph , two '' vertices'' and are called connected if contains a path from to . Otherwise, they are called disconnected. If the two vertices are additionally connected by a path of length , i.e. by a single edge, the vertices are called adjacent. A graph is said to be connected if every pair of vertices in the graph is connected. This means that there is a path between every pair of vertices. An undirected graph that is not connected is called disconnected. An undirected graph ''G'' is therefore disconnected if there exist two vertices i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
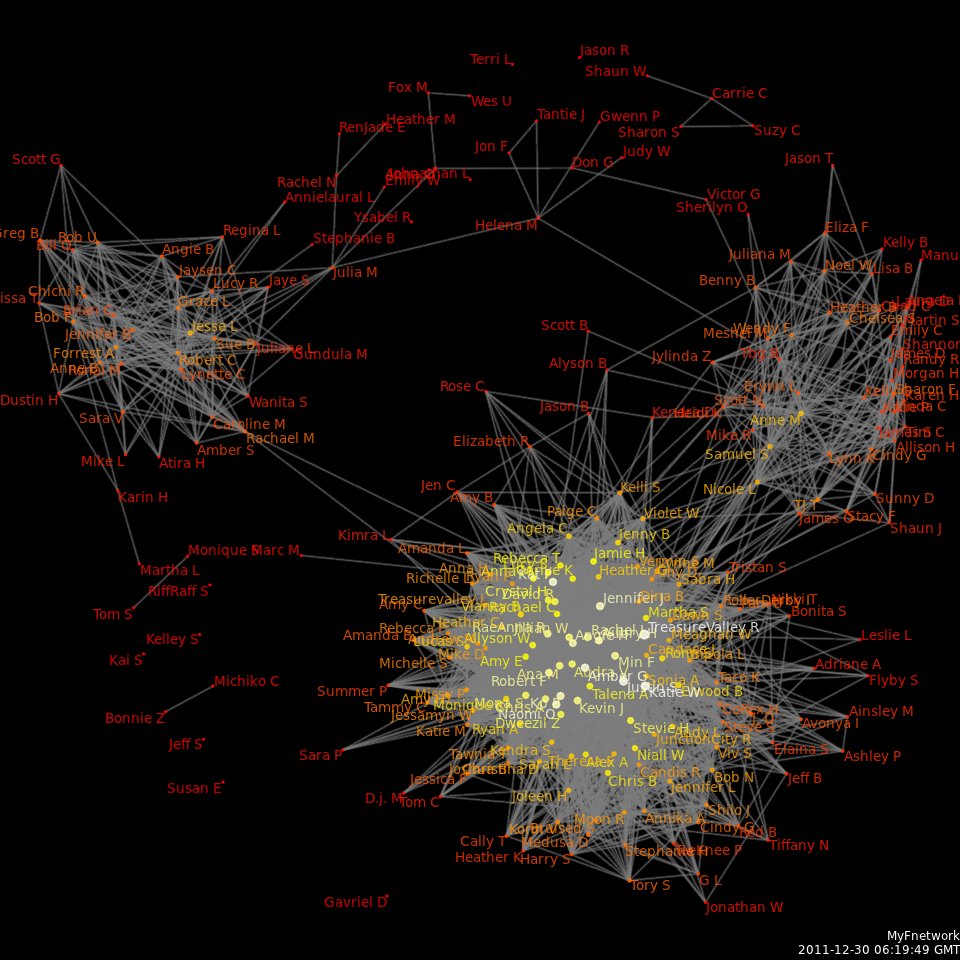
Social Network Analysis
Social network analysis (SNA) is the process of investigating social structures through the use of networks and graph theory. It characterizes networked structures in terms of ''nodes'' (individual actors, people, or things within the network) and the ''ties'', ''edges'', or ''links'' (relationships or interactions) that connect them. Examples of social structures commonly visualized through social network analysis include social media networks, memes spread, information circulation, friendship and acquaintance networks, business networks, knowledge networks, difficult working relationships, social networks, collaboration graphs, kinship, disease transmission, and sexual relationships. These networks are often visualized through ''sociograms'' in which nodes are represented as points and ties are represented as lines. These visualizations provide a means of qualitatively assessing networks by varying the visual representation of their nodes and edges to reflect attributes of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Network
A social network is a social structure made up of a set of social actors (such as individuals or organizations), sets of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities as well as a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine network dynamics. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads and "web of group affiliations". Jacob Moreno is credited with developing the first sociograms in the 1930s to study interpersonal relationships. These approaches were mathematically formalize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Community Cohesion
Community cohesion is a conceptual framework which attempts to measure the social relationships within a community. It relies on criteria such as: the presence of a shared vision, inclusion of those with diverse backgrounds, equal opportunity, and supportive relationships between individuals. It was introduced in the UK in 2001 after the 2001 England riots. The ideas contained within the framework have been refined a number of times, though the definition remains poorly defined. It has also been criticised as political in nature, with moral imperatives which are not overly helpful. History The concept of community cohesion was established in the United Kingdom following a number of riots and disturbances in England in 2001. Although the term had been used in different contexts previously (in Canada, for example), the first report to employ the term and to propose a new policy framework around it was ''Community Cohesion: The Report of The Independent Review Team''. The report con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Psychometric
Psychometrics is a field of study within psychology concerned with the theory and technique of measurement. Psychometrics generally refers to specialized fields within psychology and education devoted to testing, measurement, assessment, and related activities. Psychometrics is concerned with the objective measurement of Latent variable, latent constructs that cannot be directly observed. Examples of latent constructs include intelligence, introversion, Mental disorder, mental disorders, and Educational measurement, educational achievement. The levels of individuals on nonobservable latent variables are Statistical inference, inferred through mathematical model, mathematical modeling based on what is observed from individuals' responses to items on tests and scales. Practitioners are described as psychometricians, although not all who engage in psychometric research go by this title. Psychometricians usually possess specific qualifications such as degrees or certifications, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
K-core
In graph theory, a ''k''-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most ''k'': that is, some vertex in the subgraph touches ''k'' or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of ''k'' for which it is ''k''-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph. Degeneracy is also known as the ''k''-core number, width, and linkage, and is essentially the same as the coloring number or Szekeres–Wilf number (named after ). ''k''-degenerate graphs have also been called ''k''-inductive graphs. The degeneracy of a graph may be computed in linear time by an algorithm that repeatedly removes minimum-degree vertices. The connected components that are left after all vertices of degree less than ''k'' have been (repeatedly) removed are called the ''k''-cores of the graph and the degeneracy of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Sociological Review
The ''American Sociological Review'' is a bi-monthly peer-reviewed academic journal covering all aspects of sociology. It is published by SAGE Publications on behalf of the American Sociological Association. It was established in 1936. The editors-in-chief are Arthur S. Alderson (Indiana University-Bloomington) and Dina G. Okamoto (Indiana University-Bloomington). History For its first thirty years, the American Sociological Society (now the American Sociological Association) was largely dominated by the sociology department of the University of Chicago, and the quasi-official journal of the association was Chicago's '' American Journal of Sociology''. In 1935, the executive committee of the American Sociological Society voted 5 to 4 against disestablishing the ''American Journal of Sociology'' as the official journal of society, but the measure was passed on for consideration of the general membership, which voted 2 to 1 to establish a new journal independent of Chicago: the ''Amer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Menger's Theorem
In the mathematical discipline of graph theory, Menger's theorem says that in a finite graph, the size of a minimum cut set is equal to the maximum number of disjoint paths that can be found between any pair of vertices. Proved by Karl Menger in 1927, it characterizes the connectivity of a graph. It is generalized by the max-flow min-cut theorem, which is a weighted, edge version, and which in turn is a special case of the strong duality theorem for linear programs. Edge connectivity The edge-connectivity version of Menger's theorem is as follows: :Let ''G'' be a finite undirected graph and ''x'' and ''y'' two distinct vertices. Then the size of the minimum edge cut for ''x'' and ''y'' (the minimum number of edges whose removal disconnects ''x'' and ''y'') is equal to the maximum number of pairwise edge-independent paths from ''x'' to ''y''. :Extended to all pairs: a graph is ''k''-edge-connected (it remains connected after removing fewer than ''k'' edges) if and only if e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometimes applied to parts of the field of discrete mathematics that deals with finite se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
