|
Coherent Risk Measure
In the fields of actuarial science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance. Properties Consider a random outcome X viewed as an element of a linear space \mathcal of measurable functions, defined on an appropriate probability space. A functional \varrho : \mathcal → \R \cup \ is said to be coherent risk measure for \mathcal if it satisfies the following properties: Normalized : \varrho(0) = 0 That is, the risk when holding no assets is zero. Monotonicity : \mathrm\; Z_1,Z_2 \in \mathcal \;\mathrm\; Z_1 \leq Z_2 \; \mathrm ,\; \mathrm \; \varrho(Z_1) \geq \varrho(Z_2) That is, if portfolio Z_2 always has better values than portfolio Z_1 under almost all scenarios then the risk of Z_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Shortfall
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst q\% of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution. Expected shortfall is also called conditional value at risk (CVaR), average value at risk (AVaR), expected tail loss (ETL), and superquantile. ES estimates the risk of an investment in a conservative way, focusing on the less profitable outcomes. For high values of q it ignores the most profitable but unlikely possibilities, while for small values of q it focuses on the worst losses. On the other hand, unlike the discounted maximum loss, even for lower values of q the expected shortfall does not consider only the single most catastrophic outcome. A value of q often used in practice is 5%. Expected shortfall is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a random ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Space
In probability theory, a probability space or a probability triple (\Omega, \mathcal, P) is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die. A probability space consists of three elements:Stroock, D. W. (1999). Probability theory: an analytic view. Cambridge University Press. # A sample space, \Omega, which is the set of all possible outcomes. # An event space, which is a set of events \mathcal, an event being a set of outcomes in the sample space. # A probability function, which assigns each event in the event space a probability, which is a number between 0 and 1. In order to provide a sensible model of probability, these elements must satisfy a number of axioms, detailed in this article. In the example of the throw of a standard die, we would take the sample space to be \. For the event space, we could simply use the set of all subsets of the sampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
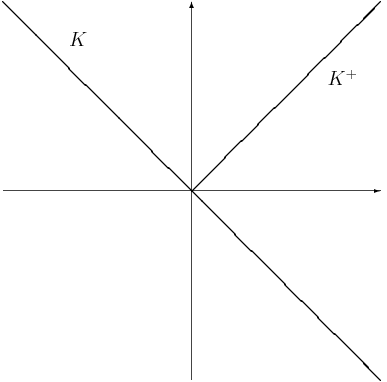
Solvency Cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the Market (economics), financial market. This is of particular interest to markets with transaction costs. Specifically, it is the convex cone of portfolios that can be exchanged to portfolios of non-negative components (including paying of any transaction costs). Mathematical basis If given a bid-ask matrix \Pi for d assets such that \Pi = \left(\pi^\right)_ and m \leq d is the number of assets which with any non-negative quantity of them can be "discarded" (traditionally m = d), then the solvency cone K(\Pi) \subset \mathbb^d is the convex cone spanned by the unit vectors e^i, 1 \leq i \leq m and the vectors \pi^e^i-e^j, 1 \leq i,j \leq d. Definition A solvency cone K is any closed convex cone such that K \subseteq \mathbb^d and K \supseteq \mathbb^d_+. Uses A process of (random) solvency cones \left\_^T is a model of a financial market. This is sometimes called a market process. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transaction Cost
In economics and related disciplines, a transaction cost is a cost in making any economic trade when participating in a market. Oliver E. Williamson defines transaction costs as the costs of running an economic system of companies, and unlike production costs, decision-makers determine strategies of companies by measuring transaction costs and production costs. Transaction costs are the total costs of making a transaction, including the cost of planning, deciding, changing plans, resolving disputes, and after-sales. Therefore, the transaction cost is one of the most significant factors in business operation and management. Oliver E. Williamson's ''Transaction Cost Economics'' popularized the concept of transaction costs. Douglass C. North argues that institutions, understood as the set of rules in a society, are key in the determination of transaction costs. In this sense, institutions that facilitate low transaction costs, boost economic growth.North, Douglass C. 1992. “Tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superhedging Price
The superhedging price is a coherent risk measure. The superhedging price of a portfolio (A) is equivalent to the smallest amount necessary to be paid for an admissible portfolio (B) at the current time so that at some specified future time the value of B is at least as great as A. In a complete market the superhedging price is equivalent to the price for hedging the initial portfolio. Mathematical definition If the set of equivalent martingale measures is denoted by EMM then the superhedging price of a portfolio ''X'' is \rho(-X) where \rho is defined by : \rho(X) = \sup_ \mathbb^Q X/math>. \rho defined as above is a coherent risk measure. Acceptance set The acceptance set for the superhedging price is the negative of the set of values of a self-financing portfolio at the terminal time. That is : A = \. Subhedging price The subhedging price is the greatest value that can be paid so that in any possible situation at the specified future time you have a second portfolio worth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Utility
In economics and finance, exponential utility is a specific form of the utility function, used in some contexts because of its convenience when risk (sometimes referred to as uncertainty) is present, in which case expected utility is maximized. Formally, exponential utility is given by: :u(c) = \begin (1-e^)/a & a \neq 0 \\ c & a = 0 \\ \end c is a variable that the economic decision-maker prefers more of, such as consumption, and a is a constant that represents the degree of risk preference (a>0 for risk aversion, a=0 for risk-neutrality, or a of final wealth ''W'' subject to :W = x'r + (W_0 - x'k) \cdot r_f where the prime sign indicates a vector transpose and where W_0 is initial wealth, ''x'' is a column vector of quantities placed in the ''n'' risky assets, ''r'' is a random vector of stochastic returns on the ''n'' assets, ''k'' is a vector of ones (so W_0 - x'k is the quantity placed in the risk-free asset), and ''r''''f'' is the known scalar return on the risk-free ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropic Risk Measure
In financial mathematics (concerned with mathematical modeling of financial markets), the entropic risk measure is a risk measure which depends on the risk aversion of the user through the exponential utility function. It is a possible alternative to other risk measures as value-at-risk or expected shortfall. It is a theoretically interesting measure because it provides different risk values for different individuals whose attitudes toward risk may differ. However, in practice it would be difficult to use since quantifying the risk aversion for an individual is difficult to do. The entropic risk measure is the prime example of a convex risk measure which is not coherent. Given the connection to utility functions, it can be used in utility maximization problems. Mathematical definition The entropic risk measure with the risk aversion parameter \theta > 0 is defined as : \rho^(X) = \frac\log\left(\mathbb ^right) = \sup_ \left\ \, where H(Q, P) = E\left frac\log\frac\right/math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Of Wang Transform Function Or Distortion Function
Sample or samples may refer to: Base meaning * Sample (statistics), a subset of a population – complete data set * Sample (signal), a digital discrete sample of a continuous analog signal * Sample (material), a specimen or small quantity of something * Sample (graphics), an intersection of a color channel and a pixel * SAMPLE history, a mnemonic acronym for questions medical first responders should ask * Product sample, a sample of a consumer product that is given to the consumer so that he or she may try a product before committing to a purchase * Standard cross-cultural sample, a sample of 186 cultures, used by scholars engaged in cross-cultural studies People *Sample (surname) *Samples (surname) * Junior Samples (1926–1983), American comedian Places * Sample, Kentucky, unincorporated community, United States * Sampleville, Ohio, unincorporated community, United States * Hugh W. and Sarah Sample House, listed on the National Register of Historic Places in Iowa, United ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a random phe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Continuous Distribution")