|
Circular Sector
A circular sector, also known as circle sector or disk sector (symbol: ⌔), is the portion of a disk (a closed region bounded by a circle) enclosed by two radii and an arc, where the smaller area is known as the ''minor sector'' and the larger being the ''major sector''. In the diagram, is the central angle, r the radius of the circle, and L is the arc length of the minor sector. The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle. Types A sector with the central angle of 180° is called a '' half-disk'' and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, such as quadrants (90°), sextants (60°), and octants (45°), which come from the sector being one 4th, 6th or 8th part of a full circle, respectively. Confusingly, the arc of a quadrant (a circular arc) can also be termed a quadrant. Compass Traditionally wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle Arc
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a '' disc''. A circle may also be defined as a special kin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octant (instrument)
The octant, also called a reflecting quadrant (instrument), quadrant, is a reflecting instrument used in navigation. Etymology The name ''octant'' derives from the Latin ''octans'' meaning ''eighth part of a circle'', because the instrument's arc is one eighth of a circle. ''Reflecting quadrant'' derives from the instrument using mirrors to reflect the path of light to the observer and, in doing so, doubles the angle measured. This allows the instrument to use a one-eighth of a Turn (geometry), turn to measure a quarter-Turn (geometry), turn or Circular sector, quadrant. Origin of the octant Newton's reflecting quadrant Isaac Newton's reflecting quadrant was invented around 1699. A detailed description of the instrument was given to Edmond Halley, but the description was not published until after Halley's death in 1742. It is not known why Halley did not publish the information during his life, as this prevented Newton from getting the credit for the invention that is gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Charles Davies (professor)
Charles Davies (January 22, 1798 – September 17, 1876) was a professor of mathematics at the United States Military Academy, notable for writing a series of mathematical textbooks. Biography Davies was born in Washington, Connecticut. His father was a County Sheriff or County Judge. During Davies' early years, the family moved to St Lawrence County, New York, where he was educated in local schools. He entered the US Military Academy at West Point in December 1813, through the influence of General Joseph Swift, who had met Davies' father during the War of 1812. Davies had earned praise for the services rendered to General James Wilkinson's army in the Descent of the St. Lawerence during the fall of 1813. Having been brought up on the frontier, Davies had had little formal education, but he had no difficulty in pursuing the courses at the academy. He graduated from the academy in December 1815. He joined the Light Artillery as a Bvt. Second Lieut. on December 11, 1815. He se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adrien-Marie Legendre
Adrien-Marie Legendre (; ; 18 September 1752 – 9 January 1833) was a French mathematician who made numerous contributions to mathematics. Well-known and important concepts such as the Legendre polynomials and Legendre transformation are named after him. Life Adrien-Marie Legendre was born in Paris on 18 September 1752 to a wealthy family. He received his education at the Collège Mazarin in Paris, and defended his thesis in physics and mathematics in 1770. He taught at the École Militaire in Paris from 1775 to 1780 and at the École Normale Supérieure, École Normale from 1795. At the same time, he was associated with the Bureau des Longitudes. In 1782, the Prussian Academy of Sciences, Berlin Academy awarded Legendre a prize for his treatise on projectiles in resistant media. This treatise also brought him to the attention of Lagrange. The ''Académie des sciences'' made Legendre an adjoint member in 1783 and an associate in 1785. In 1789, he was elected a Fellow of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Longman
Longman, also known as Pearson Longman, is a publishing company founded in London, England, in 1724 and is owned by Pearson PLC. Since 1968, Longman has been used primarily as an imprint by Pearson's Schools business. The Longman brand is also used for the Longman Schools in China and the ''Longman Dictionary''. History Beginnings The Longman company was founded by Thomas Longman (1699 – 18 June 1755), the son of Ezekiel Longman (died 1708), a gentleman of Bristol. Thomas was apprenticed in 1716 to John Osborn, a London bookseller, and at the expiration of his apprenticeship married Osborn's daughter. In August 1724, he purchased the stock and household goods of William Taylor, the first publisher of ''Robinson Crusoe'', for 9s 6d. Taylor's two shops in Paternoster Row, London, were known respectively as the '' Black Swan'' and the ''Ship'', premises at that time having signs rather than numbers, and became the publishing house premises. Longman entered into part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Quadrant
In geodesy and navigation, a meridian arc is the curve between two points on the Earth's surface having the same longitude. The term may refer either to a segment of the meridian, or to its length. The purpose of measuring meridian arcs is to determine a figure of the Earth. One or more measurements of meridian arcs can be used to infer the shape of the reference ellipsoid that best approximates the geoid in the region of the measurements. Measurements of meridian arcs at several latitudes along many meridians around the world can be combined in order to approximate a ''geocentric ellipsoid'' intended to fit the entire world. The earliest determinations of the size of a spherical Earth required a single arc. Accurate survey work beginning in the 19th century required several arc measurements in the region the survey was to be conducted, leading to a proliferation of reference ellipsoids around the world. The latest determinations use astro-geodetic measurements and the methods of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
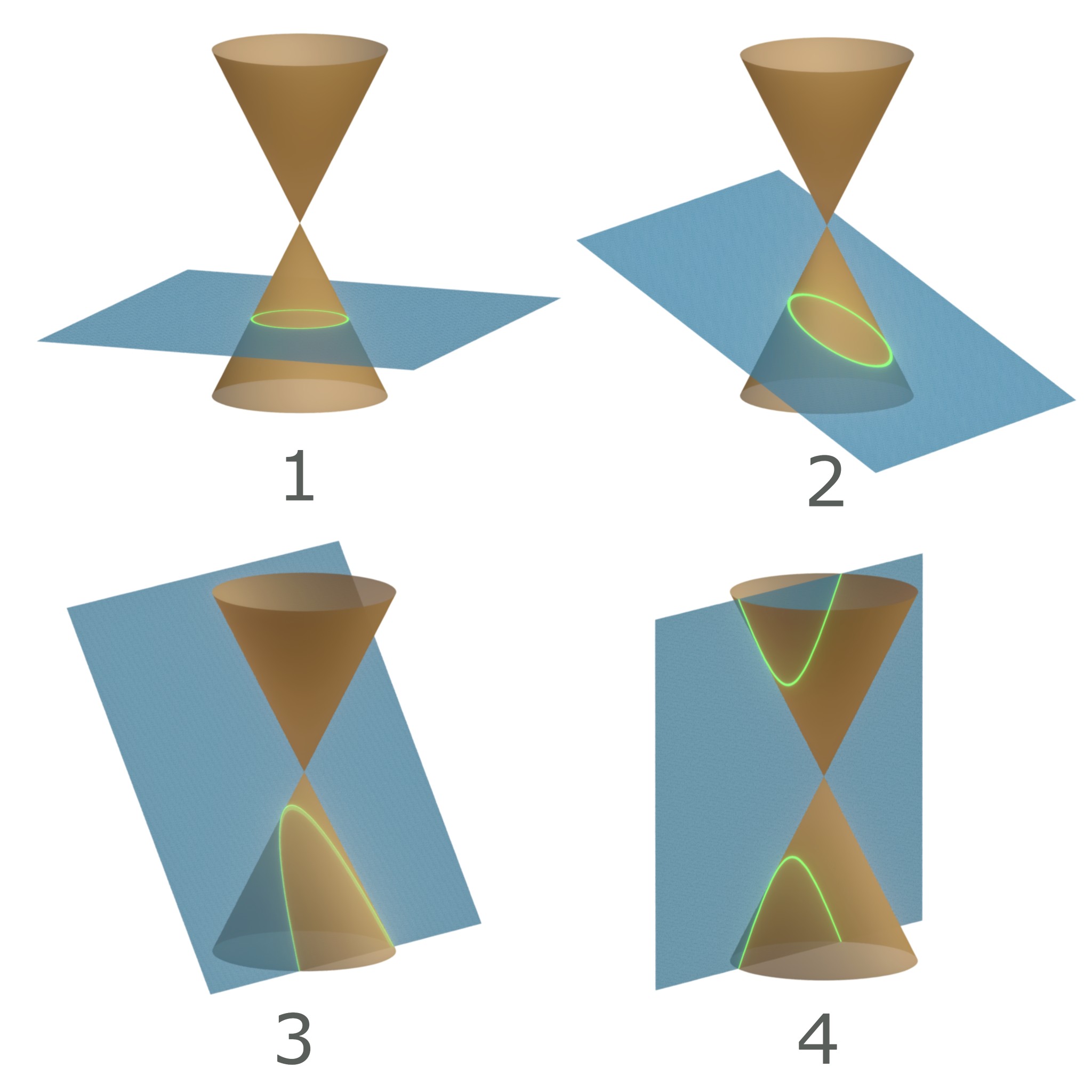
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Segment
In geometry, a circular segment (symbol: ), also known as a disk segment, is a region of a disk which is "cut off" from the rest of the disk by a secant or a chord. More formally, a circular segment is a region of two-dimensional space that is bounded by a circular arc (of less than π radians by convention) and by the circular chord connecting the endpoints of the arc. Formulae Let ''R'' be the radius of the arc which forms part of the perimeter of the segment, ''θ'' the central angle subtending the arc in radians, ''c'' the chord length, ''s'' the arc length, ''h'' the sagitta (height) of the segment, ''d'' the apothem of the segment, and ''a'' the area of the segment. Usually, chord length and height are given or measured, and sometimes the arc length as part of the perimeter, and the unknowns are area and sometimes arc length. These can't be calculated simply from chord length and height, so two intermediate quantities, the radius and central angle are usually calcula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chord (math)
A chord of a circle is a straight line segment whose endpoints both lie on a circular arc. The infinite line extension of a chord is a secant line, or just ''secant''. More generally, a chord is a line segment joining two points on any curve, for instance, an ellipse. A chord that passes through a circle's center point is the circle's diameter. The word ''chord'' is from the Latin ''chorda'' meaning ''bowstring''. In circles Among properties of chords of a circle are the following: # Chords are equidistant from the center if and only if their lengths are equal. # Equal chords are subtended by equal angles from the center of the circle. # A chord that passes through the center of a circle is called a diameter and is the longest chord of that specific circle. # If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their lengths satisfy AP·PB = CP·PD (power of a point theorem). In conics The midpoints of a set of parallel chords of a conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
West Conshohocken, Pennsylvania
West Conshohocken is a borough in Montgomery County, Pennsylvania, United States. The population was 1,320 at the 2010 census. Its sister community is Conshohocken, located across the Schuylkill River. Montgomery County's seat, Norristown, is located approximately two miles north of, and on the opposite side of the river from, West Conshohocken. History West Conshohocken Borough was incorporated October 6, 1874 from land taken almost equally from the Townships of Lower and Upper Merion. As a river borough, there existed a large number of mills and other industries utilizing water power. The Dougherty Quarry was a prosperous business, producing stone of superior quality known as ''Conshohocken'' or ''Merion Blue''. It was much sought after for public buildings, and was shipped by rail throughout the East before supplies were exhausted in the mid-twentieth century. Today, with its proximity to highways I-76 and I-476 (Blue Route), this small borough and its sister Conshohocken ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cengage
Cengage Group is an American educational content, technology, and services company for the higher education, K-12, professional, and library markets. It operates in more than 20 countries around the world.(Jun 27, 2014Global Publishing Leaders 2014: Cengage publishersweekly.comCompany Info - Wall Street JournalCengage LearningCompany Overview of Cengage Learning, Inc. BloombergBusiness Company information The company is headquartered in Boston, Massachusetts, and has approximately 5,000 employees worldwide across nearly 38 countries. It was headquartered at its Stamford, Connecticut, office until April 2014. |
Perimeter
A perimeter is a closed path that encompasses, surrounds, or outlines either a two dimensional shape or a one-dimensional length. The perimeter of a circle or an ellipse is called its circumference. Calculating the perimeter has several practical applications. A calculated perimeter is the length of fence required to surround a yard or garden. The perimeter of a wheel/circle (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter; if the length of the string was exact, it would equal the perimeter. Formulas The perimeter is the distance around a shape. Perimeters for more general shapes can be calculated, as any path, with \int_0^L \mathrms, where L is the length of the path and ds is an infinitesimal line element. Both of these must be replaced by algebraic forms in order to be practically calculated. If the perimeter is given as a closed piecewise smooth plane curve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
