|
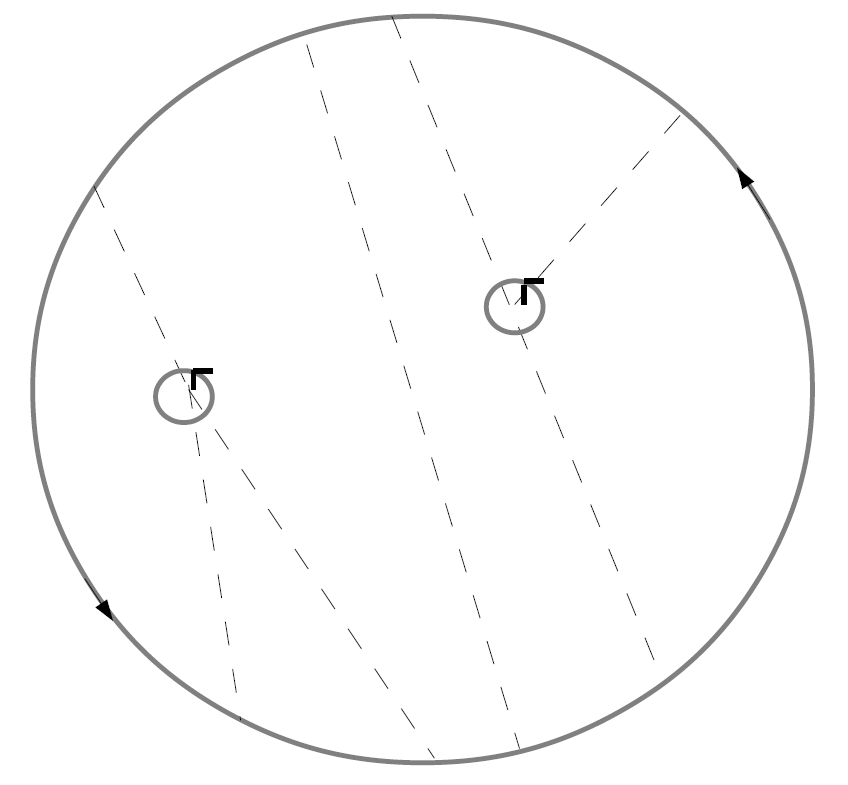
Chord Diagram (mathematics)
In mathematics, a chord diagram consists of a cyclic order on a set of objects, together with a one-to-one pairing ( perfect matching) of those objects. Chord diagrams are conventionally visualized by arranging the objects in their order around a circle, and drawing the pairs of the matching as chords of the circle. The number of different chord diagrams that may be given for a set of 2n cyclically ordered objects is the double factorial (2n-1)!!. There is a Catalan number of chord diagrams on a given ordered set in which no two chords cross each other. The crossing pattern of chords in a chord diagram may be described by a circle graph, the intersection graph of the chords: it has a vertex for each chord and an edge for each two chords that cross. In knot theory, a chord diagram can be used to describe the sequence of crossings along the planar projection of a knot, with each point at which a crossing occurs paired with the point that crosses it. To fully describe the knot, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chord Diagrams K6 Matchings
Chord or chords may refer to: Art and music * Chord (music), an aggregate of musical pitches sounded simultaneously ** Guitar chord, a chord played on a guitar, which has a particular tuning * The Chords (British band), 1970s British mod revival band * The Chords (American band), 1950s American doo-wop group * ''The Chord'' (painting), a c.1715 painting by Antoine Watteau * Andrew Chord, a comic book character who is the former mentor of the New Warriors Mathematics * Chord (geometry), a line segment joining two points on a curve * Chord (graph theory), an edge joining two nonadjacent nodes in a cycle People * Chord Overstreet, American actor and musician * Chords (musician), a Swedish hiphop/reggae artist Programming * Chord (concurrency), a concurrency construct in some object-oriented programming languages * Chord (peer-to-peer), a peer-to-peer protocol and algorithm for distributed hash tables (DHT) Science and technology * Chord (astronomy), a line crossin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Gauss Diagram
Gauss notation (also known as a Gauss code or Gauss words) is a notation for mathematical knots. It is created by enumerating and classifying the crossings of an embedding of the knot in a plane. It is named after the German mathematician Carl Friedrich Gauss (1777–1855). Gauss code represents a knot with a sequence of integers. However, rather than every crossing being represented by two different numbers, crossings are labelled with only one number. When the crossing is an overcrossing, a positive number is listed. At an undercrossing, a negative number. For example, the trefoil knot in Gauss code can be given as: 1,−2,3,−1,2,−3. Gauss code is limited in its ability to identify knots by a few problems. The starting point on the knot at which to begin tracing the crossings is arbitrary, and there is no way to determine which direction to trace in. Also, the Gauss code is unable to indicate the handedness of each crossing, which is necessary to identify a knot versus its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
International Mathematics Research Notices
The ''International Mathematics Research Notices'' is a peer-reviewed mathematics journal. Originally published by Duke University Press and Hindawi Publishing Corporation, it is now published by Oxford University Press. retrieved 2015-02-26. The Executive Editor is (). According to the '' |
European Journal Of Combinatorics
The ''European Journal of Combinatorics'' is an international peer-reviewed scientific journal that specializes in combinatorics. The journal primarily publishes papers dealing with mathematical structures within combinatorics and/or establishing direct links between combinatorics and the theories of computing. The journal includes full-length research papers, short notes, and research problems on several topics. This journal has been founded in 1980 by Michel Deza, Michel Las Vergnas and Pierre Rosenstiehl. The current editor-in-chief is Patrice Ossona de Mendez and the vice editor-in-chief is Marthe Bonamy. Abstracting and indexing The journal is abstracted and indexed in *MathSciNet, *Science Citation Index Expanded, *Scopus Scopus is a scientific abstract and citation database, launched by the academic publisher Elsevier as a competitor to older Web of Science in 2004. The ensuing competition between the two databases has been characterized as "intense" and is c . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Journal Of Statistical Planning And Inference
The ''Journal of Statistical Planning and Inference'' is a monthly peer-reviewed scientific journal covering research on statistical inference. The editors-in-chief are A. DasGupta, H. Dette and W.-L. Loh. The journal was established in 1977. According to the ''Journal Citation Reports'', the journal has a 2012 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 0.713. References External links * Statistics journals Academic journals established in 1977 Monthly journals English-language journals Elsevier academic journals {{statistics-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kontsevich Invariant
In the knot theory, mathematical theory of knots, the Kontsevich invariant, also known as the Kontsevich integral of an oriented framed link (knot theory), link, is a Finite type invariant#The universal Vassiliev invariant, universal Vassiliev invariant in the sense that any coefficient of the Kontsevich invariant is of a finite type invariant, finite type, and conversely any finite type invariant can be presented as a linear combination of such coefficients. It was defined by Maxim Kontsevich. The Kontsevich invariant is a universal quantum invariant in the sense that any quantum invariant may be recovered by substituting the appropriate #Weight system, weight system into any #Jacobi diagram and Chord diagram, Jacobi diagram. Definition The Kontsevich invariant is defined by monodromy along solutions of the Knizhnik–Zamolodchikov equations. Jacobi diagram and Chord diagram Definition Let be a circle (which is a 1-dimensional manifold). As is shown in the figure on the ri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Arrangement Of Lines
In geometry, an arrangement of lines is the subdivision of the Euclidean plane formed by a finite set of lines. An arrangement consists of bounded and unbounded convex polygons, the ''cells'' of the arrangement, line segments and rays, the ''edges'' of the arrangement, and points where two or more lines cross, the ''vertices'' of the arrangement. When considered in the projective plane rather than in the Euclidean plane, every two lines cross, and an arrangement is the projective dual to a finite set of points. Arrangements of lines have also been considered in the hyperbolic plane, and generalized to ''pseudolines'', curves that have similar topological properties to lines. The initial study of arrangements has been attributed to an 1826 paper by Jakob Steiner. An arrangement is said to be ''simple'' when at most two lines cross at each vertex, and ''simplicial'' when all cells are triangles (including the unbounded cells, as subsets of the projective plane). There are three kno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algebraic Plane Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. If the defining polynomial of a plane algebraic curve is irreducible, then one has an ''irreducible plane algebraic curve''. Otherwise, the algebraic curve is the union of one or several irreducible curves, called its ''components'', that are defined by the irreducible factors. More generally, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Singular Point Of A Curve
In geometry, a singular point on a curve is one where the curve is not given by a smooth embedding of a parameter. The precise definition of a singular point depends on the type of curve being studied. Algebraic curves in the plane Algebraic curves in the plane may be defined as the set of points satisfying an equation of the form f(x,y) = 0, where is a polynomial function If is expanded as f = a_0 + b_0 x + b_1 y + c_0 x^2 + 2c_1 xy + c_2 y^2 + \cdots If the origin is on the curve then . If then the implicit function theorem guarantees there is a smooth function so that the curve has the form near the origin. Similarly, if then there is a smooth function so that the curve has the form near the origin. In either case, there is a smooth map from to the plane which defines the curve in the neighborhood of the origin. Note that at the origin b_0 = \frac, \; b_1 = \frac, so the curve is non-singular or ''regular'' at the origin if at least one of the partial derivatives o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algebraic Geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects. The fundamental objects of study in algebraic geometry are algebraic variety, algebraic varieties, which are geometric manifestations of solution set, solutions of systems of polynomial equations. Examples of the most studied classes of algebraic varieties are line (geometry), lines, circles, parabolas, ellipses, hyperbolas, cubic curves like elliptic curves, and quartic curves like lemniscate of Bernoulli, lemniscates and Cassini ovals. These are plane algebraic curves. A point of the plane lies on an algebraic curve if its coordinates satisfy a given polynomial equation. Basic questions involve the study of points of special interest like singular point of a curve, singular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Knot Diagram
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental problem in knot the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cyclic Order
In mathematics, a cyclic order is a way to arrange a set of objects in a circle. Unlike most structures in order theory, a cyclic order is not modeled as a binary relation, such as "". One does not say that east is "more clockwise" than west. Instead, a cyclic order is defined as a ternary relation , meaning "after , one reaches before ". For example, [June, October, February], but not [June, February, October], cf. picture. A ternary relation is called a cyclic order if it is #The ternary relation, cyclic, asymmetric, transitive, and connected. Dropping the "connected" requirement results in a partial cyclic order. A set (mathematics), set with a cyclic order is called a cyclically ordered set or simply a cycle. Some familiar cycles are discrete, having only a Finite set, finite number of element (mathematics), elements: there are seven days of the week, four cardinal directions, twelve notes in the chromatic scale, and three plays in rock-paper-scissors. In a finite cycle, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |