|
Chandrasekhar Virial Equations
In astrophysics, the Chandrasekhar virial equations are a hierarchy of moment equations of the Euler equations, developed by the Indian American astrophysicist Subrahmanyan Chandrasekhar, and the physicist Enrico Fermi and Norman R. Lebovitz. Mathematical description Consider a fluid mass M of volume V with density \rho(\mathbf,t) and an isotropic pressure p(\mathbf,t) with vanishing pressure at the bounding surfaces. Here, \mathbf refers to a frame of reference attached to the center of mass. Before describing the virial equations, let's define some moments. The density moments are defined as : M = \int_V \rho \, d\mathbf, \quad I_i = \int_V \rho x_i \, d\mathbf, \quad I_ = \int_V \rho x_i x_j \, d\mathbf, \quad I_ = \int_V \rho x_i x_j x_k \, d\mathbf, \quad I_ = \int_V \rho x_i x_j x_k x_\ell \, d\mathbf, \quad \text the pressure moments are :\Pi = \int_V p \, d\mathbf, \quad \Pi_i = \int_V p x_i \, d\mathbf, \quad \Pi_ = \int_V p x_i x_j \, d\mathbf, \quad \Pi_ = \int_V p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrophysics
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the heavenly bodies, rather than their positions or motions in space–''what'' they are, rather than ''where'' they are." Among the subjects studied are the Sun, other stars, galaxies, extrasolar planets, the interstellar medium and the cosmic microwave background. Emissions from these objects are examined across all parts of the electromagnetic spectrum, and the properties examined include luminosity, density, temperature, and chemical composition. Because astrophysics is a very broad subject, ''astrophysicists'' apply concepts and methods from many disciplines of physics, including classical mechanics, electromagnetism, statistical mechanics, thermodynamics, quantum mechanics, relativity, nuclear and particle physics, and atomic and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Constant
The gravitational constant (also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant), denoted by the capital letter , is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity. In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor). The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately The modern notation of Newton's law involving was introduced in the 1890s by C. V. Boys. The first impl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet's Ellipsoidal Problem
In astrophysics, Dirichlet's ellipsoidal problem, named after Peter Gustav Lejeune Dirichlet, asks under what conditions there can exist an ellipsoidal configuration at all times of a homogeneous rotating fluid mass in which the motion, in an inertial frame, is a linear function of the coordinates. Dirichlet's basic idea was to reduce Euler equations to a system of ordinary differential equations such that the position of a fluid particle in a homogeneous ellipsoid at any time is a linear and homogeneous function of initial position of the fluid particle, using Lagrangian framework instead of the Eulerian framework. History In the winter of 1856–57, Dirichlet found some solutions of Euler equations and he presented those in his lectures on partial differential equations in July 1857 and published the results in the same month. His work was left unfinished at his sudden death in 1859, but his notes were collated and published by Richard Dedekind posthumously in 1860. Bernhard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Theorem
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by potential forces, with that of the total potential energy of the system. Mathematically, the theorem states \left\langle T \right\rangle = -\frac12\,\sum_^N \bigl\langle \mathbf_k \cdot \mathbf_k \bigr\rangle where is the total kinetic energy of the particles, represents the force on the th particle, which is located at position , and angle brackets represent the average over time of the enclosed quantity. The word virial for the right-hand side of the equation derives from ''vis'', the Latin word for "force" or "energy", and was given its technical definition by Rudolf Clausius in 1870. The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those considered in statistical mechanics; thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coriolis Force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the left of the motion of the object. In one with anticlockwise (or counterclockwise) rotation, the force acts to the right. Deflection of an object due to the Coriolis force is called the Coriolis effect. Though recognized previously by others, the mathematical expression for the Coriolis force appeared in an 1835 paper by French scientist Gaspard-Gustave de Coriolis, in connection with the theory of water wheels. Early in the 20th century, the term ''Coriolis force'' began to be used in connection with meteorology. Newton's laws of motion describe the motion of an object in an inertial (non-accelerating) frame of reference. When Newton's laws are transformed to a rotating frame of reference, the Coriolis and centrifugal accelerations appe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centrifugal Force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel to the axis of rotation and passing through the coordinate system's origin. If the axis of rotation passes through the coordinate system's origin, the centrifugal force is directed radially outwards from that axis. The magnitude of centrifugal force ''F'' on an object of mass ''m'' at the distance ''r'' from the origin of a frame of reference rotating with angular velocity is: F = m\omega^2 r The concept of centrifugal force can be applied in rotating devices, such as centrifuges, centrifugal pumps, centrifugal governors, and centrifugal clutches, and in centrifugal railways, planetary orbits and banked curves, when they are analyzed in a rotating coordinate system. Confusingly, the term has sometimes also been used for the reactiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levi-Civita Symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers; defined from the sign of a permutation of the natural numbers , for some positive integer . It is named after the Italian mathematician and physicist Tullio Levi-Civita. Other names include the permutation symbol, antisymmetric symbol, or alternating symbol, which refer to its antisymmetric property and definition in terms of permutations. The standard letters to denote the Levi-Civita symbol are the Greek lower case epsilon or , or less commonly the Latin lower case . Index notation allows one to display permutations in a way compatible with tensor analysis: \varepsilon_ where ''each'' index takes values . There are indexed values of , which can be arranged into an -dimensional array. The key defining property of the symbol is ''total antisymmetry'' in the indices. When any two indices are interchanged, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chandrasekhar Potential Energy Tensor
In astrophysics, Chandrasekhar potential energy tensor provides the gravitational potential of a body due to its own gravity created by the distribution of matter across the body, named after the Indian American astrophysicist Subrahmanyan Chandrasekhar. The Chandrasekhar tensor is a generalization of potential energy in other words, the trace of the Chandrasekhar tensor provides the potential energy of the body. Definition The Chandrasekhar potential energy tensor is defined as :W_ = -\frac \int_V \rho \Phi_ d\mathbf =\int_V \rho x_i \frac d\mathbf where :\Phi_(\mathbf) = G \int_V \rho(\mathbf) \frac d\mathbf, \quad \Rightarrow \quad \Phi_ = \Phi = G \int_V \frac d\mathbf where *G is the Gravitational constant *\Phi(\mathbf) is the self-gravitating potential from Newton's law of gravity *\Phi_ is the generalized version of \Phi *\rho(\mathbf) is the matter density distribution *V is the volume of the body It is evident that W_ is a symmetric tensor from its definition. The tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
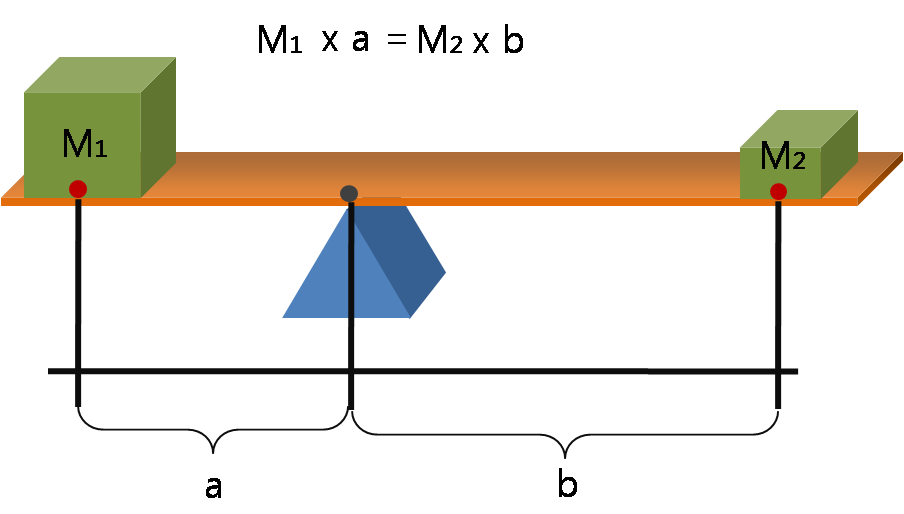
Moment (physics)
In physics, a moment is a mathematical expression involving the product of a distance and physical quantity. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In this way, the moment accounts for the quantity's location or arrangement. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enrico Fermi
Enrico Fermi (; 29 September 1901 – 28 November 1954) was an Italian (later naturalized American) physicist and the creator of the world's first nuclear reactor, the Chicago Pile-1. He has been called the "architect of the nuclear age" and the "architect of the atomic bomb". He was one of very few physicists to excel in both theoretical physics and experimental physics. Fermi was awarded the 1938 Nobel Prize in Physics for his work on induced radioactivity by neutron bombardment and for the discovery of transuranium elements. With his colleagues, Fermi filed several patents related to the use of nuclear power, all of which were taken over by the US government. He made significant contributions to the development of statistical mechanics, Quantum mechanics, quantum theory, and nuclear physics, nuclear and particle physics. Fermi's first major contribution involved the field of statistical mechanics. After Wolfgang Pauli formulated his Pauli exclusion principle, exclusion pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |