|
Centrality
In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. Definition and characterization of centrality indices Centrality indices are answers to the question "What characterizes an important vertex?" The answer is given in terms of a real-valued function on the vertices of a graph, where the values produced are expected to provide a ranking which identifies the most important nodes. The word "importance" has a wide number of meanings, leading to many di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Centrality
In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.Newman, M.E.J. 2010. ''Networks: An Introduction.'' Oxford, UK: Oxford University Press. Definition and characterization of centrality indices Centrality indices are answers to the question "What characterizes an important vertex?" The answer is given in terms of a real-valued function on the vertices of a graph, where the values produced are expected to provide a ranking which identifies the most important nodes. The word "importance" has a wide number of meanings, leading to many diff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closeness Centrality
In a connected graph, closeness centrality (or closeness) of a node is a measure of centrality in a network, calculated as the reciprocal of the sum of the length of the shortest paths between the node and all other nodes in the graph. Thus, the more central a node is, the ''closer'' it is to all other nodes. Closeness was defined by Bavelas (1950) as the reciprocal of the farness, that is: : C_B(x)= \frac. where d(y,x) is the distance (length of the shortest path) between vertices x and y. This unnormalised version of closeness is sometimes known as status When speaking of closeness centrality, people usually refer to its normalized form which represents the average length of the shortest paths instead of their sum. It is generally given by the previous formula multiplied by N-1, where N is the number of nodes in the graph resulting in: : C(x)= \frac. The normalization of closeness simplifies the comparison of nodes in graphs of different sizes. For large graphs, the minus one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betweenness Centrality
In graph theory, betweenness centrality (or "betweeness centrality") is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex. Betweenness centrality was devised as a general measure of centrality: it applies to a wide range of problems in network theory, including problems related to social networks, biology, transport and scientific cooperation. Although earlier authors have intuitively described centrality as based on betweenness, gave the first formal definition of betweenness centrality. Betweenness centrality finds wide application in network theory; it represents the degree to which nod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Betweenness Centrality
In graph theory, betweenness centrality (or "betweeness centrality") is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through (for unweighted graphs) or the sum of the weights of the edges (for weighted graphs) is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex. Betweenness centrality was devised as a general measure of centrality: it applies to a wide range of problems in network theory, including problems related to social networks, biology, transport and scientific cooperation. Although earlier authors have intuitively described centrality as based on betweenness, gave the first formal definition of betweenness centrality. Betweenness centrality finds wide application in network theory; it represents the degree to which nod ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Node Influence Metric
In graph theory and network analysis, node influence metrics are measures that rank or quantify the influence of every node (also called vertex) within a graph. They are related to centrality indices. Applications include measuring the influence of each person in a social network, understanding the role of infrastructure nodes in transportation networks, the Internet, or urban networks, and the participation of a given node in disease dynamics. Origin and development The traditional approach to understanding node importance is via centrality indicators. Centrality indices are designed to produce a ranking which accurately identifies the most influential nodes. Since the mid 2000s, however, social scientists and network physicists have begun to question the suitability of centrality indices for understanding node influence. Centralities may indicate the most influential nodes, but they are rather less informative for the vast majority of nodes which are not highly influential. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
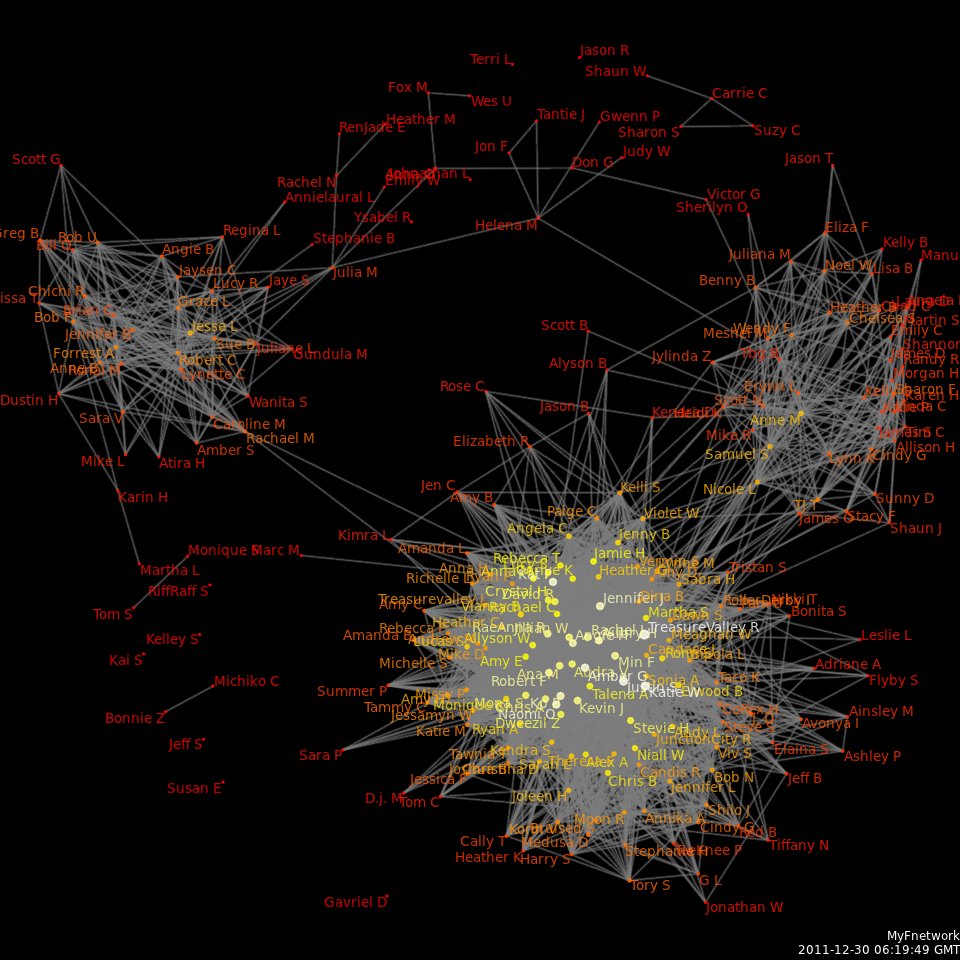
Social Network Analysis
Social network analysis (SNA) is the process of investigating social structures through the use of networks and graph theory. It characterizes networked structures in terms of ''nodes'' (individual actors, people, or things within the network) and the ''ties'', ''edges'', or ''links'' (relationships or interactions) that connect them. Examples of social structures commonly visualized through social network analysis include social media networks, memes spread, information circulation, friendship and acquaintance networks, business networks, knowledge networks, difficult working relationships, social networks, collaboration graphs, kinship, disease transmission, and sexual relationships. These networks are often visualized through '' sociograms'' in which nodes are represented as points and ties are represented as lines. These visualizations provide a means of qualitatively assessing networks by varying the visual representation of their nodes and edges to reflect attributes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvector Centrality
In graph theory, eigenvector centrality (also called eigencentrality or prestige score) is a measure of the influence of a node in a network. Relative scores are assigned to all nodes in the network based on the concept that connections to high-scoring nodes contribute more to the score of the node in question than equal connections to low-scoring nodes. A high eigenvector score means that a node is connected to many nodes who themselves have high scores. Google's PageRank and the Katz centrality are variants of the eigenvector centrality. Using the adjacency matrix to find eigenvector centrality For a given graph G:=(V,E) with , V, vertices let A = (a_) be the adjacency matrix, i.e. a_ = 1 if vertex v is linked to vertex t, and a_ = 0 otherwise. The relative centrality score, x_v, of vertex v can be defined as: : x_v = \frac 1 \lambda \sum_ x_t = \frac 1 \lambda \sum_ a_ x_t where M(v) is the set of neighbors of v and \lambda is a constant. With a small rearrangement this c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Network
A social network is a social structure made up of a set of social actors (such as individuals or organizations), sets of dyadic ties, and other social interactions between actors. The social network perspective provides a set of methods for analyzing the structure of whole social entities as well as a variety of theories explaining the patterns observed in these structures. The study of these structures uses social network analysis to identify local and global patterns, locate influential entities, and examine network dynamics. Social networks and the analysis of them is an inherently interdisciplinary academic field which emerged from social psychology, sociology, statistics, and graph theory. Georg Simmel authored early structural theories in sociology emphasizing the dynamics of triads and "web of group affiliations". Jacob Moreno is credited with developing the first sociograms in the 1930s to study interpersonal relationships. These approaches were mathematically fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Theory
Network theory is the study of graphs as a representation of either symmetric relations or asymmetric relations between discrete objects. In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes (e.g. names). Network theory has applications in many disciplines including statistical physics, particle physics, computer science, electrical engineering, biology, archaeology, economics, finance, operations research, climatology, ecology, public health, sociology, and neuroscience. Applications of network theory include logistical networks, the World Wide Web, Internet, gene regulatory networks, metabolic networks, social networks, epistemological networks, etc.; see List of network theory topics for more examples. Euler's solution of the Seven Bridges of Königsberg problem is considered to be the first true proof in the theory of networks. Network optimization N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distance (graph Theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path (also called a graph geodesic) connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite. In the case of a directed graph the distance between two vertices and is defined as the length of a shortest directed path from to consisting of arcs, provided at least one such path exists. Notice that, in contrast with the case of undirected graphs, does not necessarily coincide with —so it is just a quasi-metric, and it might be the case that one is defined while the other is not. Related concepts A metric space defined over a set of points in terms of distances in a graph defined over ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Krackhardt Kite Graph
In graph theory, the Krackhardt kite graph is a simple graph with ten nodes. The graph is named after David Krackhardt, a researcher of social network theory. Krackhardt introduced the graph in 1990 to distinguish different concepts of centrality. It has the property that the vertex with maximum degree (labeled 3 in the figure, with degree 6), the vertex with maximum betweenness centrality In graph theory, betweenness centrality (or "betweeness centrality") is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices suc ... (labeled 7), and the two vertices with maximum closeness centrality (labeled 5 and 6) are all different from each other. References {{Combin-stub Individual graphs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Freeman Centralization
Freeman, free men, or variant, may refer to: * a member of the Third Estate in medieval society (commoners), see estates of the realm * Freeman, an apprentice who has been granted freedom of the company, was a rank within Livery companies * Freeman, in Middle English synonymous with franklin (class), initially a person not tied to land as a villein or serf, later a land-owner * Freeman (Colonial), in U.S. colonial times, a person not under legal restraint * A person who has been awarded Freedom of the City * Free tenant, a social class in the Middle Ages * Freedman, a former slave that had been freed from bondage Places ;In the United States * Freeman, Georgia, an unincorporated community * Freeman, Illinois, an unincorporated community * Freeman, Indiana, an unincorporated community * Freeman, South Dakota, a city * Freeman, Virginia, an unincorporated community * Freeman, Wisconsin, a town in Crawford County * Freeman, Langlade County, Wisconsin, an unincorporated commu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
