|
Cellular Automaton
A cellular automaton (pl. cellular automata, abbrev. CA) is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling. A cellular automaton consists of a regular grid of ''cells'', each in one of a finite number of '' states'', such as ''on'' and ''off'' (in contrast to a coupled map lattice). The grid can be in any finite number of dimensions. For each cell, a set of cells called its ''neighborhood'' is defined relative to the specified cell. An initial state (time ''t'' = 0) is selected by assigning a state for each cell. A new ''generation'' is created (advancing ''t'' by 1), according to some fixed ''rule'' (generally, a mathematical function) that determines the new state of e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rule 110
The Rule 110 cellular automaton (often called simply Rule 110) is an elementary cellular automaton with interesting behavior on the boundary between stability and chaos. In this respect, it is similar to Conway's Game of Life. Like Life, Rule 110 with a particular repeating background pattern is known to be Turing complete. This implies that, in principle, any calculation or computer program can be simulated using this automaton. Definition In an elementary cellular automaton, a one-dimensional pattern of 0s and 1s evolves according to a simple set of rules. Whether a point in the pattern will be 0 or 1 in the new generation depends on its current value, as well as on those of its two neighbors. The Rule 110 automaton has the following set of rules: The name "Rule 110" derives from the fact that this rule can be summarized in the binary sequence 01101110; interpreted as a binary number, this corresponds to the decimal value 110. History In 2004, Matthew Cook published a pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modular Arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book ''Disquisitiones Arithmeticae'', published in 1801. A familiar use of modular arithmetic is in the 12-hour clock, in which the day is divided into two 12-hour periods. If the time is 7:00 now, then 8 hours later it will be 3:00. Simple addition would result in , but clocks "wrap around" every 12 hours. Because the hour number starts over at zero when it reaches 12, this is arithmetic ''modulo'' 12. In terms of the definition below, 15 is ''congruent'' to 3 modulo 12, so "15:00" on a 24-hour clock is displayed "3:00" on a 12-hour clock. Congruence Given an integer , called a modulus, two integers and are said to be congruent modulo , if is a divisor of their difference (that is, if there is an integer such that ). Congruence modulo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensions
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categories and refer to absolute space and time. That conception of the world is a four-dimensional space but not the one that was found necessa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
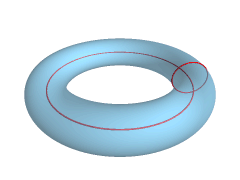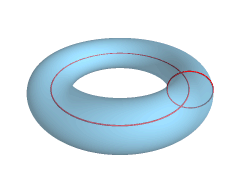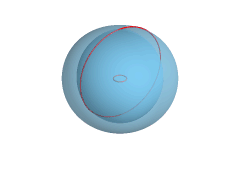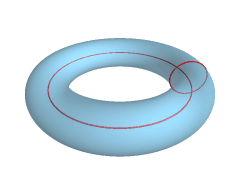
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of ''perpendicularity''. By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in other fields including art and chemistry. Etymology The word comes from the Ancient Greek ('), meaning "upright", and ('), meaning "angle". The Ancient Greek (') and Classical Latin ' originally denoted a rectangle. Later, they came to mean a right triangle. In the 12th century, the post-classical Latin word ''orthogonalis'' came to mean a right angle or something related to a right angle. Mathematics Physics * In optics, polarization states are said to be orthogonal when they propagate independently of each other, as in vertical and horizontal linear polarization or right- and left-handed circular polarization. * In special relativity, a time axis determined by a rapidity of motion is hyperbolic-orthogonal to a space axis of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Paper
Graph paper, coordinate paper, grid paper, or squared paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting graphs of functions or experimental data and drawing curves. It is commonly found in mathematics and engineering education settings and in laboratory notebooks. Graph paper is available either as loose leaf paper or bound in notebooks. History The Metropolitan Museum of Art owns a pattern book dated to around 1596 in which each page bears a grid printed with a woodblock. The owner has used these grids to create block pictures in black and white and in colour. The first commercially published "coordinate paper" is usually attributed to a Dr. Buxton of England, who patented paper, printed with a rectangular coordinate grid, in 1794. A century later, E. H. Moore, a distinguished mathematician at the University of Chicago, advocated usage of paper with "squared lines" by students of high schools an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann Neighborhood
In cellular automata, the von Neumann neighborhood (or 4-neighborhood) is classically defined on a two-dimensional square lattice and is composed of a central cell and its four adjacent cells. The neighborhood is named after John von Neumann, who used it to define the von Neumann cellular automaton and the von Neumann universal constructor within it. It is one of the two most commonly used neighborhood types for two-dimensional cellular automata, the other one being the Moore neighborhood. This neighbourhood can be used to define the notion of 4-connected pixels in computer graphics.. The von Neumann neighbourhood of a cell is the cell itself and the cells at a Manhattan distance of 1. The concept can be extended to higher dimensions, for example forming a 6-cell octahedral neighborhood for a cubic cellular automaton in three dimensions. Von Neumann neighborhood of range ''r'' An extension of the simple von Neumann neighborhood described above is to take the set of poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moore Neighborhood
In cellular automata, the Moore neighborhood is defined on a two-dimensional square lattice and is composed of a central cell and the eight cells that surround it. Name The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. Importance It is one of the two most commonly used neighborhood types, the other one being the von Neumann neighborhood, which excludes the corner cells. The well known Conway's Game of Life, for example, uses the Moore neighborhood. It is similar to the notion of 8-connected pixels in computer graphics. The Moore neighbourhood of a cell is the cell itself and the cells at a Chebyshev distance of 1. The concept can be extended to higher dimensions, for example forming a 26-cell cubic neighborhood for a cellular automaton in three dimensions, as used by 3D Life. In dimension ''d,'' where 0 \le d, d \in \mathbb, the size of the neighborhood is 3''d'' − 1. In two dimensions, the number of cells in an ''ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turing Machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algorithm. The machine operates on an infinite memory tape divided into discrete cells, each of which can hold a single symbol drawn from a finite set of symbols called the alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right, or halts the computation. The choice of which replacement symbol to write and which direction to move is based on a finite table that specifies what to do for each comb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |