|
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor \boldsymbol\sigma, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components \sigma_ that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector e to the traction vector T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sigma_e_i, or, :\leftright\leftrightcdot \leftright The SI units of both stress tensor and traction vector are N/m2, corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of materi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Components Stress Tensor Cartesian
Circuit Component may refer to: •Are devices that perform functions when they are connected in a circuit. In engineering, science, and technology Generic systems *System components, an entity with discrete structure, such as an assembly or software module, within a system considered at a particular level of analysis *Lumped element model, a model of spatially distributed systems Electrical *Component video, a type of analog video information that is transmitted or stored as two or more separate signals *Electronic components, the constituents of electronic circuits * Symmetrical components, in electrical engineering, analysis of unbalanced three-phase power systems Mathematics *Color model, a way of describing how colors can be represented, typically as multiple values or color components *Component (group theory), a quasi-simple subnormal sub-group *Connected component (graph theory), a maximal connected subgraph *Connected component (topology), a maximal connected s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Momentum Equation
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum. Main equation In convective (or Lagrangian) form the Cauchy momentum equation is written as: : \frac = \frac 1 \rho \nabla \cdot \boldsymbol + \mathbf where * \mathbf is the flow velocity vector field, which depends on time and space, (unit: \mathrm) * t is time, (unit: \mathrm) * \frac is the material derivative of \mathbf, equal to \partial_t\mathbf + \mathbf\cdot \nabla\mathbf, (unit: \mathrm) * \rho is the density at a given point of the continuum (for which the continuity equation holds), (unit: \mathrm) * \boldsymbol is the stress tensor, (unit: \mathrm) * \mathbf=\beginf_x\\ f_y\\ f_z\end is a vector containing all of the accelerations caused by body forces (sometimes simply gravitational acceleration), (unit: \mathrm) * \nabla\cdot\boldsymbol= \begin \dfrac + \dfrac + \dfrac \\ \dfrac + \dfrac + \dfrac \\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Force
Surface force denoted ''fs'' is the force that acts across an internal or external surface element in a material body. Surface force can be decomposed into two perpendicular components: normal forces and shear forces. A normal force acts normally over an area and a shear force acts tangentially over an area. Equations for surface force Surface force due to pressure : f_s=p \cdot A \ , where ''f'' = force, ''p'' = pressure, and ''A'' = area on which a uniform pressure acts Examples Pressure related surface force Since pressure is \frac=\mathrm , and area is a (length)\cdot(width) = \mathrm= \mathrm , :a pressure of 5\ \mathrm = 5\ \mathrm over an area of 20\ \mathrm will produce a surface force of (5\ \mathrm) \cdot (20\ \mathrm) = 100\ \mathrm . See also *Body force *Contact force A contact force is any force that occurs as a result of two objects making contact with each other. Contact forces are ubiquitous and are responsible for most visible inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a push or a pull. A force has both magnitude and direction, making it a vector quantity. It is measured in the SI unit of newton (N). Force is represented by the symbol (formerly ). The original form of Newton's second law states that the net force acting upon an object is equal to the rate at which its momentum changes with time. If the mass of the object is constant, this law implies that the acceleration of an object is directly proportional to the net force acting on the object, is in the direction of the net force, and is inversely proportional to the mass of the object. Concepts related to force include: thrust, which increases the velocity of an object; drag, which decreases the velocity of an object; and torque, which produce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress Vector
In continuum mechanics, the Cauchy stress tensor \boldsymbol\sigma, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components \sigma_ that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector e to the traction vector T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sigma_e_i, or, :\leftright\leftrightcdot \leftright The SI units of both stress tensor and traction vector are N/m2, corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of materia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Forces In Continuum 2
{{disambig ...
Internal may refer to: * Internality as a concept in behavioural economics * Neijia, internal styles of Chinese martial arts * Neigong or "internal skills", a type of exercise in meditation associated with Daoism *'' Internal (album)'' by Safia, 2016 See also * * Internals (other) *External (other) External may refer to: * External (mathematics), a concept in abstract algebra * Externality In economics, an externality or external cost is an indirect cost or benefit to an uninvolved third party that arises as an effect of another party' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Forces In Continuum
{{disambig ...
Internal may refer to: * Internality as a concept in behavioural economics * Neijia, internal styles of Chinese martial arts * Neigong or "internal skills", a type of exercise in meditation associated with Daoism *'' Internal (album)'' by Safia, 2016 See also * * Internals (other) *External (other) External may refer to: * External (mathematics), a concept in abstract algebra * Externality In economics, an externality or external cost is an indirect cost or benefit to an uninvolved third party that arises as an effect of another party' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Stresses And Stress Invariants
Principal may refer to: Title or rank * Principal (academia), the chief executive of a university ** Principal (education), the office holder/ or boss in any school * Principal (civil service) or principal officer, the senior management level in the UK Civil Service * Principal dancer, the top rank in ballet * Principal (music), the top rank in an orchestra Law * Principal (commercial law), the person who authorizes an agent ** Principal (architecture), licensed professional(s) with ownership of the firm * Principal (criminal law), the primary actor in a criminal offense * Principal (Catholic Church), an honorific used in the See of Lisbon Places * Principal, Cape Verde, a village * Principal, Ecuador, a parish Media * ''The Principal'' (TV series), a 2015 Australian drama series * ''The Principal'', a 1987 action film * Principal (music), the lead musician in a section of an orchestra * Principal photography, the first phase of movie production * "The Principal", a song on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
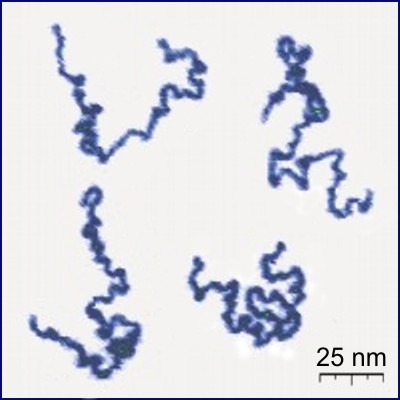
Polymers
A polymer (; Greek '' poly-'', "many" + ''-mer'', "part") is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic and natural polymers play essential and ubiquitous roles in everyday life. Polymers range from familiar synthetic plastics such as polystyrene to natural biopolymers such as DNA and proteins that are fundamental to biological structure and function. Polymers, both natural and synthetic, are created via polymerization of many small molecules, known as monomers. Their consequently large molecular mass, relative to small molecule compounds, produces unique physical properties including toughness, high elasticity, viscoelasticity, and a tendency to form amorphous and semicrystalline structures rather than crystals. The term "polymer" derives from the Greek word πολύς (''polus'', meaning "many, much") and μέρος (''meros'', meani ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |