Carnot's Theorem
Carnot's theorem or Carnot's principle may refer to: In geometry: *Carnot's theorem (inradius, circumradius), describing a property of the incircle and the circumcircle of a triangle *Carnot's theorem (conics), describing a relation between triangles and conic sections *Carnot's theorem (perpendiculars), describing a property of certain perpendiculars on triangle sides In physics: *Carnot's theorem (thermodynamics), setting a maximum efficiency obtainable from a heat engine See also * Carnot cycle A Carnot cycle is an ideal thermodynamic cycle proposed by French physicist Sadi Carnot in 1824 and expanded upon by others in the 1830s and 1840s. By Carnot's theorem, it provides an upper limit on the efficiency of any classical thermodynam ...

Carnot's Theorem (inradius, Circumradius)
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter ''D'' to the sides of an arbitrary triangle ''ABC'' is :DF + DG + DH = R + r,\ where ''r'' is the inradius and ''R'' is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment ''DX'' (''X'' = ''F'', ''G'', ''H'') lies completely outside the triangle. In the diagram, ''DF'' is negative and both ''DG'' and ''DH'' are positive. The theorem is named after Lazare Carnot (1753–1823). It is used in a proof of the Japanese theorem for concyclic polygons. References *Claudi Alsina, Roger B. Nelsen: ''When Less is More: Visualizing Basic Inequalities''. MAA, 2009, , 99*Frédéric Perrier: ''Carnot's Theorem in Trigonometric Disguise''. The Mathematical Gazette, Volume 91, No. 520 (March, 2007), pp. 115–117JSTOR *David Richeson''The Japanese Theorem for Nonconvex Polygons – Carnot's Theorem'' Convergenc ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Carnot's Theorem (conics)
Carnot's theorem (named after Lazare Carnot) describes a relation between conic sections and triangle A triangle is a polygon with three Edge (geometry), edges and three Vertex (geometry), vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, an ...s. In a triangle ABC with points C_A, C_B on the side AB, A_B, A_C on the side BC and B_C, B_A on the side AC those six points are located on a common conic section if and only if the following equation holds: : \frac\cdot \frac\cdot \frac\cdot \frac \cdot \frac\cdot \frac=1 . References *Huub P.M. van Kempen''On Some Theorems of Poncelet and Carnot'' Forum Geometricorum, Volume 6 (2006), pp. 229–234. *Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: ''Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie''. Springer 2016, {{ISBN, 9783662530344, pp. 40, 168–173 (German) External links ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

Carnot's Theorem (perpendiculars)
Carnot's theorem (named after Lazare Carnot) describes a necessary and sufficient condition for three lines that are perpendicular to the (extended) sides of a triangle having a common point of intersection. The theorem can also be thought of as a generalization of the Pythagorean theorem In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t .... Theorem For a triangle \triangle ABC with sides a, b, c consider three lines that are perpendicular to the triangle sides and intersect in a common point F. If P_a, P_b, P_c are the pedal points of those three perpendiculars on the sides a, b, c, then the following equation holds: : , AP_c, ^2+, BP_a, ^2+, CP_b, ^2=, BP_c, ^2+, CP_a, ^2+, AP_b, ^2 The converse of the statement above is true as well, that is if the equation holds for the peda ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

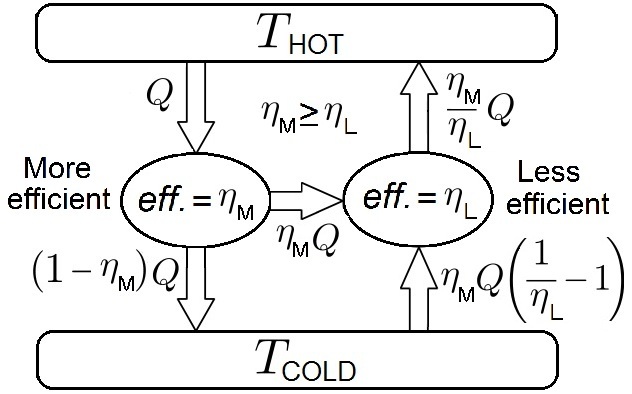
Carnot's Theorem (thermodynamics)
In thermodynamics, Carnot's theorem, developed in 1824 by Nicolas Léonard Sadi Carnot, also called Carnot's rule, is a principle that specifies limits on the maximum efficiency that any heat engine can obtain. Carnot's theorem states that all heat engines operating between the same two thermal or heat reservoirs can't have efficiencies greater than a reversible heat engine operating between the same reservoirs. A corollary of this theorem is that every reversible heat engine operating between a pair of heat reservoirs is equally efficient, regardless of the working substance employed or the operation details. Since a Carnot heat engine is also a reversible engine, the efficiency of all the reversible heat engines is determined as the efficiency of the Carnot heat engine that depends solely on the temperatures of its hot and cold reservoirs. The maximum efficiency (i.e., the Carnot heat engine efficiency) of a heat engine operating between cold and hot reservoirs, denoted as ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]