|
CAL Actor Language
CAL (the Cal Actor Language) is a high-level programming languageCAL Language Report: Specification of the CAL actor language, Johan Eker and Jörn W. Janneck, Technical Memorandum No. UCB/ERL M03/48, University of California, Berkeley, CA, 94720, USA, December 1, 2003 for writing (dataflow) actors, which are stateful operators that transform input streams of data objects (tokens) into output streams. CAL has been compiled to a variety of target platforms, including single-core processors, multicore processors, and programmable hardware. It has been used in several application areas, including video and processing, compression and cryptography. The MPEG Reconfigurable Video Coding (RVC)Overview of the MPEG Reconfigurable Video Coding Framework, Shuvra S. Bhattacharyya, Johan Eker, Jörn W. Janneck, Christophe Lucarz, Marco Mattavelli, Mickaël Raulet, ''Journal of Signal Processing Systems, 2009, Springer'' working group has adopted CAL as part of their standardization efforts. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dataflow Programming
In computer programming, dataflow programming is a programming paradigm that models a program as a directed graph of the data flowing between operations, thus implementing dataflow principles and architecture. Dataflow programming languages share some features of functional languages, and were generally developed in order to bring some functional concepts to a language more suitable for numeric processing. Some authors use the term ''datastream'' instead of ''dataflow'' to avoid confusion with dataflow computing or dataflow architecture, based on an indeterministic machine paradigm. Dataflow programming was pioneered by Jack Dennis and his graduate students at MIT in the 1960s. Considerations Traditionally, a program is modelled as a series of operations happening in a specific order; this may be referred to as sequential, procedural, control flow (indicating that the program chooses a specific path), or imperative programming. The program focuses on commands, in line with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Unary Operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. This is in contrast to ''binary operations'', which use two operands. An example is any function , where is a set; the function is a unary operation on . Common notations are prefix notation (e.g. ¬, −), postfix notation (e.g. factorial ), functional notation (e.g. or ), and superscripts (e.g. transpose ). Other notations exist as well, for example, in the case of the square root, a horizontal bar extending the square root sign over the argument can indicate the extent of the argument. Examples Absolute value Obtaining the absolute value of a number is a unary operation. This function is defined as , n, = \begin n, & \mbox n\geq0 \\ -n, & \mbox n<0 \end where is the absolute value of . Negation |
Expression (computer Science)
In computer science, an expression is a Syntax (programming languages), syntactic entity in a programming language that may be evaluated to determine its value (computer science), value. It is a combination of one or more Constant (programming), constants, variable (programming), variables, function (programming), functions, and operator (programming), operators that the programming language interprets (according to its particular Order of operations, rules of precedence and of Associative property, association) and computes to produce ("to return", in a state (computer science), stateful environment) another value. This process, for mathematical expressions, is called ''evaluation''. In simple settings, the return type, resulting value is usually one of various primitive data type, primitive types, such as string (computer science), string, boolean expression, boolean, or numerical (such as integer (computer science), integer, floating-point number, floating-point, or complex data t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numerical Digit
A numerical digit (often shortened to just digit) or numeral is a single symbol used alone (such as "1"), or in combinations (such as "15"), to represent numbers in positional notation, such as the common base 10. The name "digit" originates from the Latin ''digiti'' meaning fingers. For any numeral system with an integer base, the number of different digits required is the absolute value of the base. For example, decimal (base 10) requires ten digits (0 to 9), and binary (base 2) requires only two digits (0 and 1). Bases greater than 10 require more than 10 digits, for instance hexadecimal (base 16) requires 16 digits (usually 0 to 9 and A to F). Overview In a basic digital system, a numeral is a sequence of digits, which may be of arbitrary length. Each position in the sequence has a place value, and each digit has a value. The value of the numeral is computed by multiplying each digit in the sequence by its place value, and summing the results. Di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ada (programming Language)
Ada is a structured, statically typed, imperative, and object-oriented high-level programming language, inspired by Pascal and other languages. It has built-in language support for '' design by contract'' (DbC), extremely strong typing, explicit concurrency, tasks, synchronous message passing, protected objects, and non-determinism. Ada improves code safety and maintainability by using the compiler to find errors in favor of runtime errors. Ada is an international technical standard, jointly defined by the International Organization for Standardization (ISO), and the International Electrotechnical Commission (IEC). , the standard, ISO/IEC 8652:2023, is called Ada 2022 informally. Ada was originally designed by a team led by French computer scientist Jean Ichbiah of Honeywell under contract to the United States Department of Defense (DoD) from 1977 to 1983 to supersede over 450 programming languages then used by the DoD. Ada was named after Ada Lovelace (1815–185 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Java (programming Language)
Java is a High-level programming language, high-level, General-purpose programming language, general-purpose, Memory safety, memory-safe, object-oriented programming, object-oriented programming language. It is intended to let programmers ''write once, run anywhere'' (Write once, run anywhere, WORA), meaning that compiler, compiled Java code can run on all platforms that support Java without the need to recompile. Java applications are typically compiled to Java bytecode, bytecode that can run on any Java virtual machine (JVM) regardless of the underlying computer architecture. The syntax (programming languages), syntax of Java is similar to C (programming language), C and C++, but has fewer low-level programming language, low-level facilities than either of them. The Java runtime provides dynamic capabilities (such as Reflective programming, reflection and runtime code modification) that are typically not available in traditional compiled languages. Java gained popularity sh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
PASCAL (database)
PASCAL is a scientific bibliographic database, which is maintained by INIST The Institut de l'information scientifique et technique, or INIST () is the CNRS centre of documentation located in France. It has as mission to collect, treat and diffuse results of scientific and technical research. The INIST produces three bi ... ( CNRS). PASCAL covers the core scientific literature in science, technology and medicine with a special emphasis on European literature. , PASCAL maintains a database of more than 17 million records, 90% of which are author abstracts. Its coverage is from 1973 to present. Its source documents are composed of journal articles at 88% (3,085 international titles), proceedings at 9%, and dissertations, books, patents, and reports account combined for 3%. References External links * Bibliographic databases and indexes French National Centre for Scientific Research {{database-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
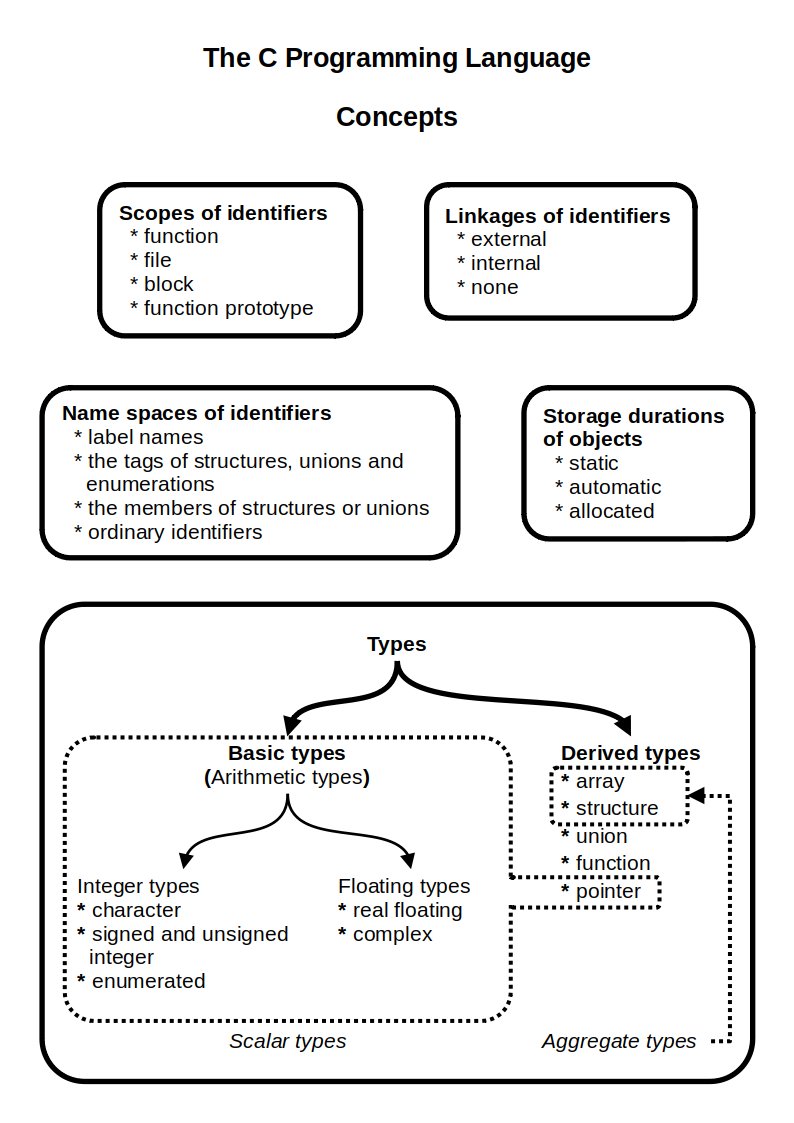
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Syntactic Sugar
In computer science, syntactic sugar is syntax within a programming language that is designed to make things easier to read or to express. It makes the language "sweeter" for human use: things can be expressed more clearly, more concisely, or in an alternative style that some may prefer. Syntactic sugar is usually a shorthand for a common operation that could also be expressed in an alternate, more verbose, form: The programmer has a choice of whether to use the shorter form or the longer form, but will usually use the shorter form since it is shorter and easier to type and read. For example, many programming languages provide special syntax for referencing and updating array elements. Abstractly, an array reference is a procedure of two arguments: an array and a subscript vector, which could be expressed as get_array(Array, vector(i,j)). Instead, many languages provide syntax such as Array ,j/code>. Similarly an array element update is a procedure consisting of three arguments, fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nondeterminism
Nondeterminism or nondeterministic may refer to: Computer science *Nondeterministic programming *Nondeterministic algorithm *Nondeterministic model of computation **Nondeterministic finite automaton **Nondeterministic Turing machine *Indeterminacy in computation Other *Indeterminism Indeterminism is the idea that events (or certain events, or events of certain types) are not caused, or are not caused deterministically. It is the opposite of determinism and related to chance. It is highly relevant to the philosophical pr ... (philosophy) See also * Indeterminacy (other) {{Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Operator (computer Programming)
In computer programming, an operator is a programming language construct that provides functionality that may not be possible to define as a user-defined function (i.e. sizeof in C) or has syntax different than a function (i.e. infix addition as in a+b). Like other programming language concepts, ''operator'' has a generally accepted, although debatable meaning among practitioners while at the same time each language gives it specific meaning in that context, and therefore the meaning varies by language. Some operators are represented with symbols characters typically not allowed for a function identifier to allow for presentation that is more familiar looking than typical function syntax. For example, a function that tests for greater-than could be named gt, but many languages provide an infix symbolic operator so that code looks more familiar. For example, this: if gt(x, y) then return Can be: if x > y then return Some languages allow a language-defined operator t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |