|
Wiener Process
In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown (Scottish botanist from Montrose), Robert Brown. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary increments, stationary independent increments) and occurs frequently in pure and applied mathematics, economy, economics, quantitative finance, evolutionary biology, and physics. The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingale (probability theory), martingales. It is a key process in terms of which more complicated sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
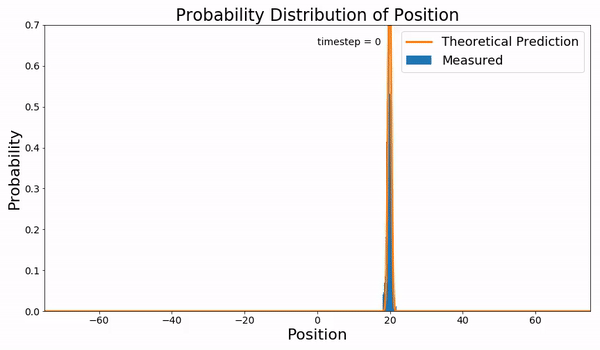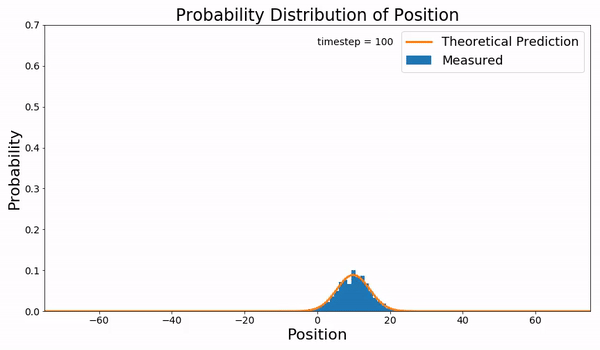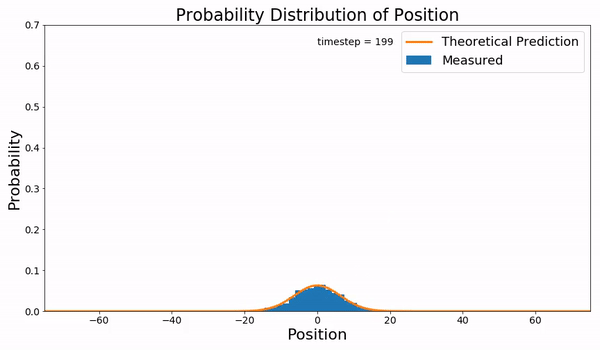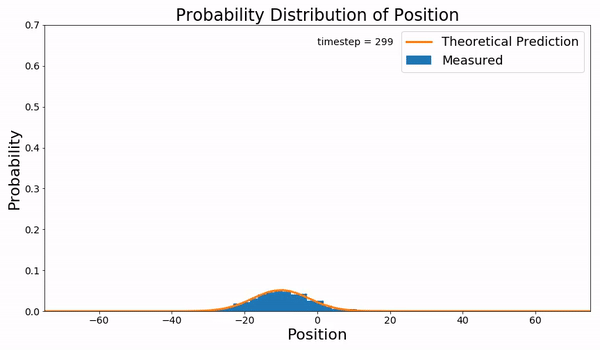
Wiener Process Zoom
Wiener (from German: "wikt:Viennese, Viennese") may refer to: Food * A Polish sausage (kielbasa) or "wenar" * A Vienna sausage of German origin, named after the capital of Austria * A hot dog, a cooked sausage, traditionally grilled or steamed and served in a sliced bun People * Wiener (surname) Places *Wiener Neudorf, a town in the eastern part of the Mödling district, Austria *Wiener Neustadt, a town south of Vienna, in the state of Lower Austria, Austria *Wiener Stadthalle, an indoor arena, in Vienna, Austria *Wiener Staatsoper, the Vienna State Opera Other uses *The Wiener AC, also known as Wiener AC or WAC, an Austrian sports club in Vienna * Wiener process, a mathematical model related to Brownian motion * Wiener equation, named after Norbert Wiener, assumes the current velocity of a fluid particle fluctuates randomly * Wiener filter, a noise filter used in signal processing * Wiener (crater), a crater on the far side of the Moon *''Wiener Bonbons'', a waltz by Johan St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martingale (probability Theory)
In probability theory, a martingale is a sequence of random variables (i.e., a stochastic process) for which, at a particular time, the conditional expectation of the next value in the sequence is equal to the present value, regardless of all prior values. History Originally, '' martingale'' referred to a class of betting strategies that was popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins their stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double their bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, their probability of eventually flipping heads approaches 1, which makes the martingale betting strategy seem like a sure thing. However, the exponential growth of the bets eventually bankrupts its users due to f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langevin Equation
In physics, a Langevin equation (named after Paul Langevin) is a stochastic differential equation describing how a system evolves when subjected to a combination of deterministic and fluctuating ("random") forces. The dependent variables in a Langevin equation typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, which models the fluctuating motion of a small particle in a fluid. Brownian motion as a prototype The original Langevin equation describes Brownian motion, the apparently random movement of a particle in a fluid due to collisions with the molecules of the fluid, m\frac=-\lambda \mathbf+\boldsymbol\left( t\right). Here, \mathbf is the velocity of the particle, and m is its mass. The force acting on the particle is written as a sum of a viscous force ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single schem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control system eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Filter (signal Processing)
In signal processing, a filter is a device or process that removes some unwanted components or features from a signal. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies or frequency bands. However, filters do not exclusively act in the frequency domain; especially in the field of image processing many other targets for filtering exist. Correlations can be removed for certain frequency components and not for others without having to act in the frequency domain. Filters are widely used in electronics and telecommunication, in radio, television, audio recording, radar, control systems, music synthesis, image processing, and computer graphics. There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Filters may be: *non-linear or linear *time-variant or t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brownian Noise
] In science, Brownian noise, also known as Brown noise or red noise, is the type of signal noise produced by Brownian motion, hence its alternative name of random walk noise. The term "Brown noise" does not come from the color, but after Robert Brown, who documented the erratic motion for multiple types of inanimate particles in water. The term "red noise" comes from the "white noise"/"white light" analogy; red noise is strong in longer wavelengths, similar to the red end of the visible spectrum. Explanation The graphic representation of the sound signal mimics a Brownian pattern. Its spectral density is inversely proportional to ''f'' 2, meaning it has higher intensity at lower frequencies, even more so than pink noise. It decreases in intensity by 6 dB per octave (20 dB per decade) and, when heard, has a "damped" or "soft" quality compared to white and pink noise. The sound is a low roar resembling a waterfall or heavy rainfall. See also violet noise, which is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronics Engineering
Electronics engineering is a sub-discipline of electrical engineering which emerged in the early 20th century and is distinguished by the additional use of active components such as semiconductor devices to amplify and control electric current flow. Previously electrical engineering only used passive devices such as mechanical switches, resistors, inductors and capacitors. It covers fields such as: analog electronics, digital electronics, consumer electronics, embedded systems and power electronics. It is also involved in many related fields, for example solid-state physics, radio engineering, telecommunications, control systems, signal processing, systems engineering, computer engineering, instrumentation engineering, electric power control, robotics. The Institute of Electrical and Electronics Engineers (IEEE) is one of the most important professional bodies for electronics engineers in the US; the equivalent body in the UK is the Institution of Engineering and Technology (IET ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
White Noise
In signal processing, white noise is a random signal having equal intensity at different frequencies, giving it a constant power spectral density. The term is used, with this or similar meanings, in many scientific and technical disciplines, including physics, acoustical engineering, telecommunications, and statistical forecasting. White noise refers to a statistical model for signals and signal sources, rather than to any specific signal. White noise draws its name from white light, although light that appears white generally does not have a flat power spectral density over the visible band. In discrete time, white noise is a discrete signal whose samples are regarded as a sequence of serially uncorrelated random variables with zero mean and finite variance; a single realization of white noise is a random shock. Depending on the context, one may also require that the samples be independent and have identical probability distribution (in other words independent and iden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schramm–Loewner Evolution
In probability theory, the Schramm–Loewner evolution with parameter ''κ'', also known as stochastic Loewner evolution (SLE''κ''), is a family of random planar curves that have been proven to be the scaling limit of a variety of two-dimensional lattice models in statistical mechanics. Given a parameter ''κ'' and a domain in the complex plane ''U'', it gives a family of random curves in ''U'', with ''κ'' controlling how much the curve turns. There are two main variants of SLE, ''chordal SLE'' which gives a family of random curves from two fixed boundary points, and ''radial SLE'', which gives a family of random curves from a fixed boundary point to a fixed interior point. These curves are defined to satisfy conformal invariance and a domain Markov property. It was discovered by as a conjectured scaling limit of the planar uniform spanning tree (UST) and the planar loop-erased random walk (LERW) probabilistic processes, and developed by him together with Greg Lawler and Wendel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
