|
Curie's Law
For many paramagnetic materials, the magnetization of the material is directly proportional to an applied magnetic field, for sufficiently high temperatures and small fields. However, if the material is heated, this proportionality is reduced. For a fixed value of the field, the magnetic susceptibility is inversely proportional to temperature, that is : M = \chi H, \quad \chi = \frac, where : \chi>0 is the (volume) magnetic susceptibility, : M is the magnitude of the resulting magnetization ( A/ m), : H is the magnitude of the applied magnetic field (A/m), : T is absolute temperature ( K), : C is a material-specific Curie constant (K). Pierre Curie discovered this relation, now known as Curie's law, by fitting data from experiment. It only holds for high temperatures and weak magnetic fields. As the derivations below show, the magnetization saturates in the opposite limit of low temperatures and strong fields. If the Curie constant is null, other magnetic effects dominate, like ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paramagnetism
Paramagnetism is a form of magnetism whereby some materials are weakly attracted by an externally applied magnetic field, and form internal, induced magnetic fields in the direction of the applied magnetic field. In contrast with this behavior, diamagnetic materials are repelled by magnetic fields and form induced magnetic fields in the direction opposite to that of the applied magnetic field. Paramagnetic materials include most chemical elements and some compounds; they have a relative magnetic permeability slightly greater than 1 (i.e., a small positive magnetic susceptibility) and hence are attracted to magnetic fields. The magnetic moment induced by the applied field is linear in the field strength and rather weak. It typically requires a sensitive analytical balance to detect the effect and modern measurements on paramagnetic materials are often conducted with a SQUID magnetometer. Paramagnetism is due to the presence of unpaired electrons in the material, so most atom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Free Energy
In thermodynamics, the Gibbs free energy (or Gibbs energy as the recommended name; symbol is a thermodynamic potential that can be used to calculate the maximum amount of Work (thermodynamics), work, other than Work (thermodynamics)#Pressure–volume work, pressure–volume work, that may be performed by a closed system, thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as G(p,T) = U + pV - TS = H - TS where: * U is the internal energy of the system * H is the enthalpy of the system * S is the entropy of the system * T is the temperature of the system * V is the volume of the system * p is the pressure of the system (which must be equal to that of the surroundings for mechanical equilibrium). The Gibbs free energy change (, measured in joules in International System of Units, SI) is the ''maximum'' amount of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Position (vector)
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector res ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brillouin Function
The Brillouin and Langevin functions are a pair of special functions that appear when studying an idealized paramagnetic material in statistical mechanics. These functions are named after French physicists Paul Langevin and Léon Brillouin who contributed to the microscopic understanding of magnetic properties of matter. The Langevin function is derived using statistical mechanics, and describes how magnetic dipoles are aligned by an applied field. The Brillouin function was developed later to give an explanation that considers quantum physics. The Langevin function could then be a seen as a special case of the more general Brillouin function if the quantum number J would be infinite (J \to \infty ). Brillouin function for paramagnetism The Brillouin function arises when studying magnetization of an ideal paramagnet. In particular, it describes the dependency of the magnetization M on the applied magnetic field B, defined by the following equation: The function B_J is usually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Units
Gaussian units constitute a metric system of units of measurement. This system is the most common of the several electromagnetic unit systems based on the centimetre–gram–second system of units (CGS). It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units. The term "cgs units" is ambiguous and therefore to be avoided if possible: there are several variants of CGS, which have conflicting definitions of electromagnetic quantities and units. International System of Units, SI units predominate in most fields, and continue to increase in popularity at the expense of Gaussian units. Alternative unit systems also exist. Conversions between quantities in the Gaussian and SI systems are direct unit conversions, because the quantities themselves are defined differently in each system. This means that the equations that express physical laws of electromagnetism—such as Maxwell's equations—will change depending on the system of quantities that is emp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Total Angular Momentum Quantum Number
In quantum mechanics, the total angular momentum quantum number parametrises the total angular momentum of a given particle, by combining its orbital angular momentum and its intrinsic angular momentum (i.e., its spin). If s is the particle's spin angular momentum and ℓ its orbital angular momentum vector, the total angular momentum j is \mathbf j = \mathbf s + \boldsymbol ~. The associated quantum number is the main total angular momentum quantum number ''j''. It can take the following range of values, jumping only in integer steps: \vert \ell - s\vert \le j \le \ell + s where ''ℓ'' is the azimuthal quantum number (parameterizing the orbital angular momentum) and ''s'' is the spin quantum number (parameterizing the spin). The relation between the total angular momentum vector j and the total angular momentum quantum number ''j'' is given by the usual relation (see angular momentum quantum number) \Vert \mathbf j \Vert = \sqrt \, \hbar The vector's ''z''-projection is giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Introduction To Solid State Physics
''Introduction to Solid State Physics'', known colloquially as ''Kittel'', is a classic condensed matter physics textbook written by American physicist Charles Kittel in 1953. The book has been highly influential and has seen widespread adoption; Marvin L. Cohen remarked in 2019 that Kittel's content choices in the original edition played a large role in defining the field of solid-state physics. It was also the first proper textbook covering this new field of physics. The book is published by John Wiley and Sons and, as of 2018, it is in its ninth edition and has been reprinted many times as well as translated into over a dozen languages, including Chinese, French, German, Hungarian, Indonesian, Italian, Japanese, Korean, Malay, Romanian, Russian, Spanish, and Turkish. In some later editions, the eighteenth chapter, titled ''Nanostructures'', was written by Paul McEuen. Along with its competitor '' Ashcroft and Mermin'', the book is considered a standard textbook in condensed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
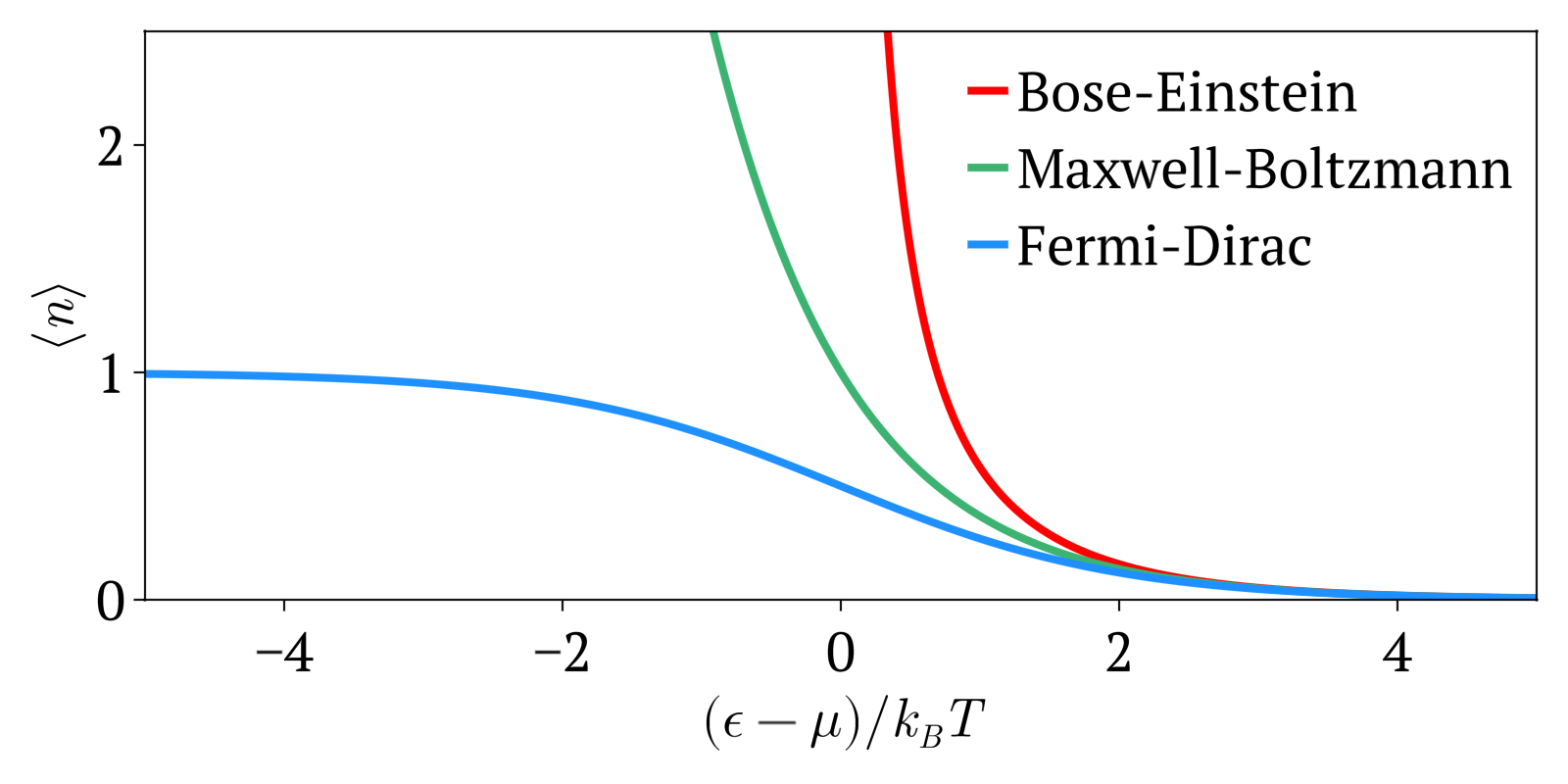
Fermi–Dirac Statistics
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics. Fermi–Dirac statistics applies to identical and indistinguishable particles with half-integer spin (1/2, 3/2, etc.), called fermions, in thermodynamic equilibrium. For the case of negligible interaction between particles, the system can be described in terms of single-particle energy states. A result is the Fermi–Dirac distribution of particles over these states where no two particles can occupy the same state, which has a considerable effect on the properties of the system. Fermi� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Exclusion Principle
In quantum mechanics, the Pauli exclusion principle (German: Pauli-Ausschlussprinzip) states that two or more identical particles with half-integer spins (i.e. fermions) cannot simultaneously occupy the same quantum state within a system that obeys the laws of quantum mechanics. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940. In the case of electrons in atoms, the exclusion principle can be stated as follows: in a poly-electron atom it is impossible for any two electrons to have the same two values of ''all'' four of their quantum numbers, which are: ''n'', the principal quantum number; ', the azimuthal quantum number; ''m'', the magnetic quantum number; and ''ms'', the spin quantum number. For example, if two electrons reside in the same orbital, then their values of ''n'', ', and ''m'' are equal. In that case, the two values of ''m''s (spin) pair must be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Surface
In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied electron states from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic band structure, electronic energy bands. The existence of a Fermi surface is a direct consequence of the Pauli exclusion principle, which allows a maximum of one electron per quantum state. The study of the Fermi surfaces of materials is called fermiology. Theory Consider a Spin (physics), spin-less ideal Fermi gas of N particles. According to Fermi–Dirac statistics, the mean occupation number of a state with energy \epsilon_i is given by : \langle n_i\rangle =\frac, where * \left\langle n_i\right\rangle is the mean occupation number of the ith state * \epsilon_i is the kinetic energy of the ith state * \mu is the chemical potential (at zero temperature, this is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curie Constant
Curie may refer to: *Curie family, a family of distinguished scientists: :* Jacques Curie (1856–1941), French physicist, Pierre's brother :* Pierre Curie (1859–1906), French physicist and Nobel Prize winner, Marie's husband :* Marie Skłodowska–Curie (1867–1934), Polish chemist and physicist, two-time Nobel Prize winner, Pierre's wife :* Irène Joliot-Curie (1897–1956), French physicist and Nobel Prize winner, Pierre and Marie's daughter :* Frédéric Joliot-Curie (1900–1958), French physicist and Nobel Prize winner, Irène's husband :*Ève Curie (1904–2007), French-American journalist and pianist, Pierre and Marie's daughter :* Henry Richardson Labouisse (1904–1987), American diplomat and director of UNICEF, Ève's husband Things and ideas named after the Curie family Scientific concepts, inventions and discoveries * Curie (unit) (Ci), unit of radioactivity * Curie (lunar crater) * Curie (Martian crater) * Curie (rocket engine), a liquid-propellant engine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Tangent
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Diction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |