|
Cox–Ingersoll–Ross Model
In mathematical finance, the Cox–Ingersoll–Ross (CIR) model describes the evolution of interest rates. It is a type of "one factor model" ( short-rate model) as it describes interest rate movements as driven by only one source of market risk. The model can be used in the valuation of interest rate derivatives. It was introduced in 1985 by John C. Cox, Jonathan E. Ingersoll and Stephen A. Ross as an extension of the Vasicek model. The model The CIR model specifies that the instantaneous interest rate r_t follows the stochastic differential equation, also named the CIR Process: :dr_t = a(b-r_t)\, dt + \sigma\sqrt\, dW_t where W_t is a Wiener process (modelling the random market risk factor) and a , b , and \sigma\, are the parameters. The parameter a corresponds to the speed of adjustment to the mean b , and \sigma\, to volatility. The drift factor, a(b-r_t), is exactly the same as in the Vasicek model. It ensures mean reversion of the interest rate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ornstein–Uhlenbeck Process
In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck. The Ornstein–Uhlenbeck process is a stationary Gauss–Markov process, which means that it is a Gaussian process, a Markov process, and is temporally homogeneous. In fact, it is the only nontrivial process that satisfies these three conditions, up to allowing linear transformations of the space and time variables. Over time, the process tends to drift towards its mean function: such a process is called mean-reverting. The process can be considered to be a modification of the random walk in continuous time, or Wiener process, in which the properties of the process have been changed so that there is a tendency of the walk to move back towa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chen Model
In finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" (short-rate model) as it describes interest rate movements as driven by three sources of market risk. It was the first stochastic mean and stochastic volatility model and it was published in 1994 by Lin Chen, economist, theoretical physicist and former lecturer/professor at Beijing Institute of Technology, Yonsei University of Korea, and Nanyang Tech University of Singapore. The dynamics of the instantaneous interest rate are specified by the stochastic differential equations: : dr_t = \kappa(\theta_t-r_t)\,dt + \sqrt\,\sqrt\, dW_1, : d \theta_t = \nu(\zeta-\theta_t)\,dt + \alpha\,\sqrt\, dW_2, : d \sigma_t = \mu(\beta-\sigma_t)\,dt + \eta\,\sqrt\, dW_3. In an authoritative review of modern finance (''Continuous-Time Methods in Finance: A Review and an Assessment''), the Chen model is listed along with the models of Robert C. Merton, Oldrich Vasi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed-form Expression
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th root, exponent, logarithm, trigonometric functions, and inverse hyperbolic functions), but usually no limit, differentiation, or integration. The set of operations and functions may vary with author and context. Example: roots of polynomials The solutions of any quadratic equation with complex coefficients can be expressed in closed form in terms of addition, subtraction, multiplication, division, and square root extraction, each of which is an elementary function. For example, the quadratic equation :ax^2+bx+c=0, is tractable since its solutions can be expressed as a closed-form expression, i.e. in terms of elementary functions: :x=\frac. Similarly, solutions of cubic and quartic (third and fourth degree) equations can be expresse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basic Affine Jump Diffusion
In mathematics probability theory, a basic affine jump diffusion (basic AJD) is a stochastic process Z of the form : dZ_t=\kappa (\theta -Z_t)\,dt+\sigma \sqrt\,dB_t+dJ_t,\qquad t\geq 0, Z_\geq 0, where B is a standard Brownian motion, and J is an independent compound Poisson process with constant jump intensity l and independent exponentially distributed jumps with mean \mu . For the process to be well defined, it is necessary that \kappa \theta \geq 0 and \mu \geq 0 . A basic AJD is a special case of an affine process and of a jump diffusion. On the other hand, the Cox–Ingersoll–Ross (CIR) process is a special case of a basic AJD. Basic AJDs are attractive for modeling default times in credit risk applications, since both the moment generating function : m\left( q\right) =\operatorname \left( e^\right) ,\qquad q\in \mathbb, and the characteristic function : \varphi \left( u\right) =\operatorname \left( e^\right) ,\qquad u\in \mathbb, are known in close ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discretization
In applied mathematics, discretization is the process of transferring continuous functions, models, variables, and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers. Dichotomization is the special case of discretization in which the number of discrete classes is 2, which can approximate a continuous variable as a binary variable (creating a dichotomy for modeling purposes, as in binary classification). Discretization is also related to discrete mathematics, and is an important component of granular computing. In this context, ''discretization'' may also refer to modification of variable or category ''granularity'', as when multiple discrete variables are aggregated or multiple discrete categories fused. Whenever continuous data is discretized, there is always some amount of discretization error. The goal is to reduce the amount to a level conside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Simulation
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.DLOUHÝ, M.; FÁBRY, J.; KUNCOVÁ, M.. Simulace pro ekonomy. Praha : VŠE, 2005. Realizations of these random variables are generated and inserted into a model of the system. Outputs of the model are recorded, and then the process is repeated with a new set of random values. These steps are repeated until a sufficient amount of data is gathered. In the end, the distribution of the outputs shows the most probable estimates as well as a frame of expectations regarding what ranges of values the variables are more or less likely to fall in. Often random variables inserted into the model are created on a computer with a random number generator (RNG). The U(0,1) uniform distribution outputs of the random number generator are then transformed into random variables with probability distributions that are used in the system model. Etymology '' St ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimation theory, estimating the Statistical parameter, parameters of an assumed probability distribution, given some observed data. This is achieved by Mathematical optimization, maximizing a likelihood function so that, under the assumed statistical model, the Realization (probability), observed data is most probable. The point estimate, point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is Differentiable function, differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Least Squares
In statistics, ordinary least squares (OLS) is a type of linear least squares method for choosing the unknown parameters in a linear regression model (with fixed level-one effects of a linear function of a set of explanatory variables) by the principle of least squares: minimizing the sum of the squares of the differences between the observed dependent variable (values of the variable being observed) in the input dataset and the output of the (linear) function of the independent variable. Geometrically, this is seen as the sum of the squared distances, parallel to the axis of the dependent variable, between each data point in the set and the corresponding point on the regression surface—the smaller the differences, the better the model fits the data. The resulting estimator can be expressed by a simple formula, especially in the case of a simple linear regression, in which there is a single regressor on the right side of the regression equation. The OLS estimator is consiste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Reversion (finance)
Mean reversion is a financial term for the assumption that an asset's price will tend to converge to the average price over time. Using mean reversion as a timing strategy involves both the identification of the trading range for a security and the computation of the average price using quantitative methods. Mean reversion is a phenomenon that can be exhibited in a host of financial time-series data, from price data, earnings data, and book value. When the current market price is less than the average past price, the security is considered attractive for purchase, with the expectation that the price will rise. When the current market price is above the average past price, the market price is expected to fall. In other words, deviations from the average price are expected to revert to the average. This knowledge serves as the cornerstone of multiple trading strategies. Stock reporting services commonly offer moving averages for periods such as 50 and 100 days. While reporting ser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
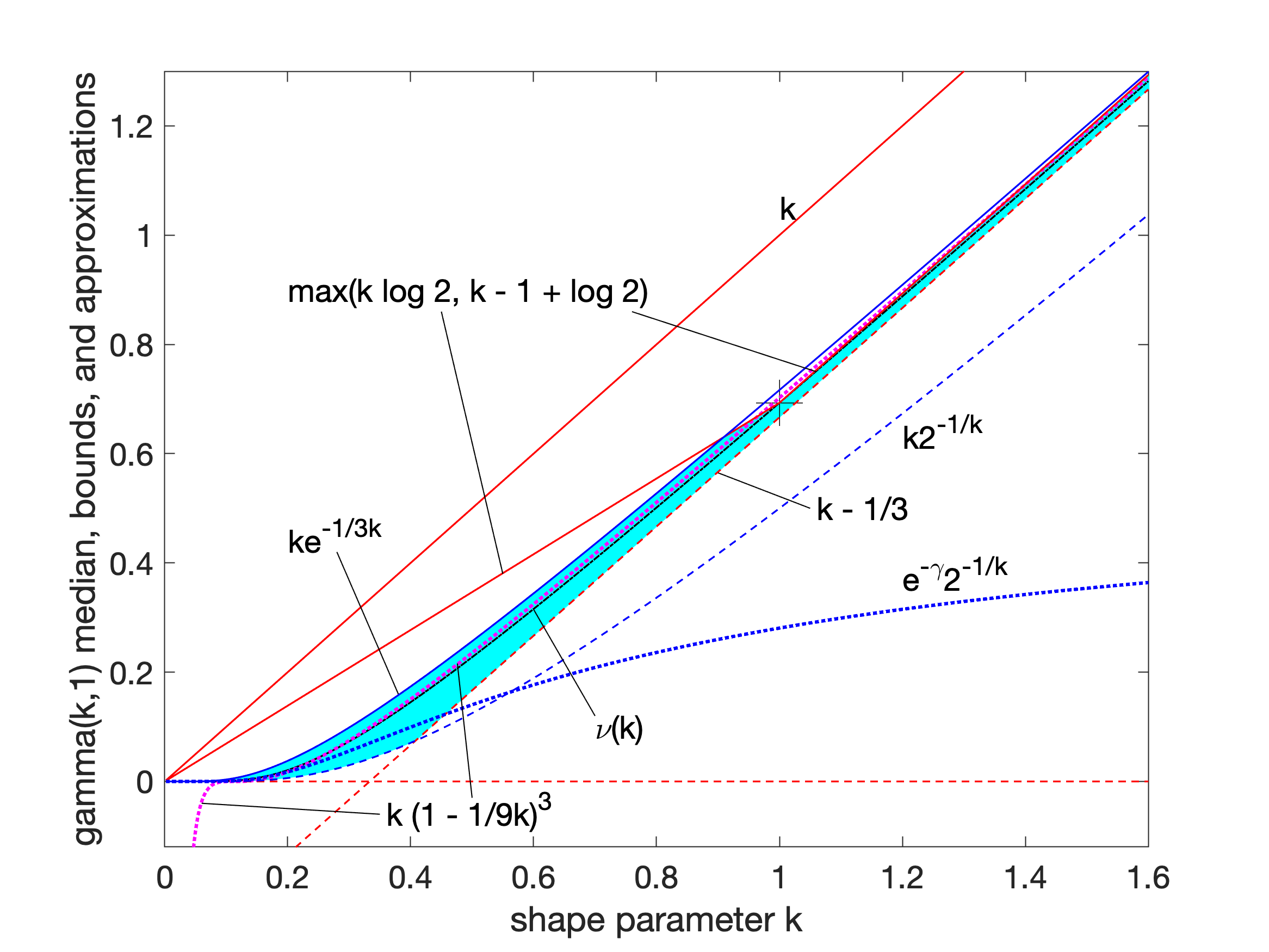
Gamma Distribution
In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common in econo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
