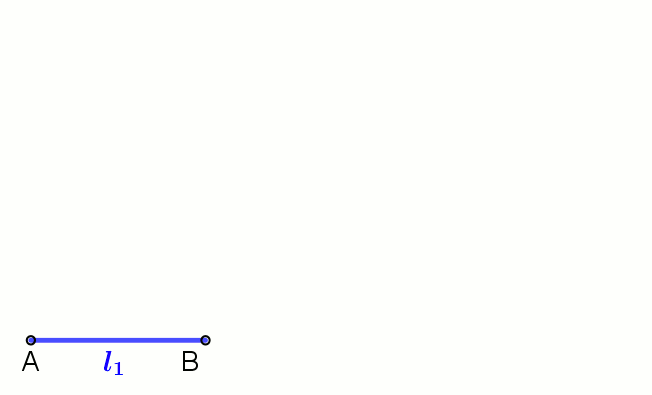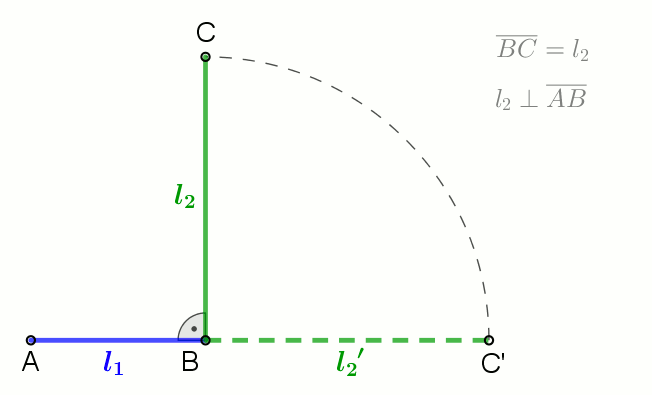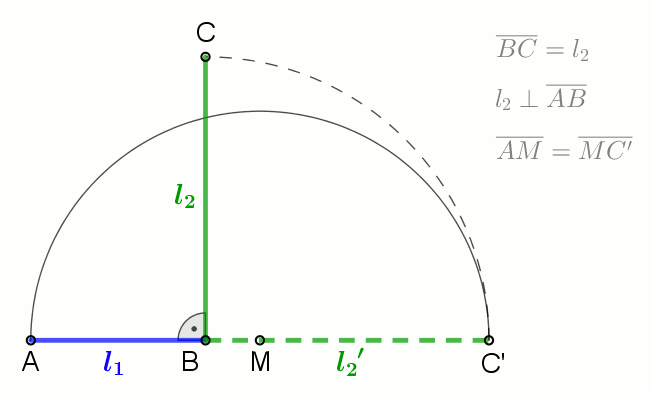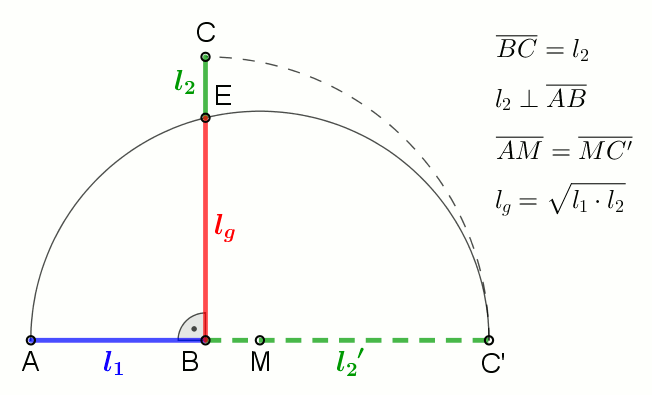|
Coordinate Systems For The Hyperbolic Plane
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used. This article tries to give an overview of several coordinate systems in use for the two-dimensional hyperbolic plane. In the descriptions below the constant Gaussian curvature of the plane is −1. Sinh, cosh and tanh are hyperbolic functions. Polar coordinate system The polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian system) is called the ''pole'', and the ray from the pole in the reference direction is the ''polar axis''. The distance from the pole is called the ''radial coordinate'' or ''radius'', and the angle is called the ''angular coordinate'', or ''polar angl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P'' not on ''R'', in the plane containing both line ''R'' and point ''P'' there are at least two distinct lines through ''P'' that do not intersect ''R''. (Compare the above with Playfair's axiom, the modern version of Euclid's parallel postulate.) Hyperbolic plane geometry is also the geometry of pseudospherical surfaces, surfaces with a constant negative Gaussian curvature. Saddle surfaces have negative Gaussian curvature in at least some regions, where they locally resemble the hyperbolic plane. A modern use of hyperbolic geometry is in the theory of special relativity, particularly the Minkowski model. When geometers first realised they were working with something other than the standard Euclidean geometry, they described thei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a set of numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometric mean is defined as the th root of the product of numbers, i.e., for a set of numbers , the geometric mean is defined as :\left(\prod_^n a_i\right)^\frac = \sqrt /math> or, equivalently, as the arithmetic mean in logscale: :\exp For instance, the geometric mean of two numbers, say 2 and 8, is just the square root of their product, that is, \sqrt = 4. As another example, the geometric mean of the three numbers 4, 1, and 1/32 is the cube root of their product (1/8), which is 1/2, that is, \sqrt = 1/2. The geometric mean applies only to positive numbers. The geometric mean is often used for a set of numbers whose values are meant to be multiplied together or are exponential in nature, such as a set of growth figures: values of the human population or int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nikolai Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, Никола́й Ива́нович Лобаче́вский, p=nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; – ) was a Russian mathematician and geometer, known primarily for his work on hyperbolic geometry, otherwise known as Lobachevskian geometry, and also for his fundamental study on Dirichlet integrals, known as the Lobachevsky integral formula. William Kingdon Clifford called Lobachevsky the "Copernicus of Geometry" due to the revolutionary character of his work. Biography Nikolai Lobachevsky was born either in or near the city of Nizhny Novgorod in the Russian Empire (now in Nizhny Novgorod Oblast, Russia) in 1792 to parents of Russian and Polish origin – Ivan Maksimovich Lobachevsky and Praskovia Alexandrovna Lobachevskaya.Victor J. Katz. ''A history of mathematics: Introduction''. Addison-Wesley. 2009. p. 842. Stephen Hawking. ''God Created the Integers: The Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axial Coordinates
{{disambiguation ...
Axial may refer to: * one of the anatomical directions describing relationships in an animal body * In geometry: :* a geometric term of location :* an axis of rotation * In chemistry, referring to an axial bond * a type of modal frame, in music * axial-flow, a type of fan * the Axial Age in China, India, etc. * Axial Seamount and submarine volcano off Oregon, USA * Axial, Colorado, a ghost town See also *Axiality (other) *Axis (other) An axis (plural ''axes'') is an imaginary line around which an object rotates or is symmetrical. Axis may also refer to: Mathematics * Axis of rotation: see rotation around a fixed axis *Axis (mathematics), a designator for a Cartesian-coordinate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circles About The Origin In Hyperbolic Axial Coordinates
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with r=0 (a single point) is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted. Specifically, a circle is a simple closed curve that divides the plane into two regions: an interior and an exterior. In everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the figure, or to the whole figure including its interior; in strict technical usage, the circle is only the boundary and the whole figure is called a ''disc''. A circle may also be defined as a special kind o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter ''O'', used as a fixed point of reference for the geometry of the surrounding space. In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer. This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry. Cartesian coordinates In a Cartesian coordinate system, the origin is the point where the axes of the system intersect.. The origin divides each of these axes into two halves, a positive and a negative semiaxis. Points can then be located with reference to the origin by giving their numerical coordinates—that is, the positions of their projections along each axis, either in the positive or negative direction. The coordinates of the origin are always all zero, for example (0,0) in two dimensions and (0,0,0) in three. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Point
In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line ''l'' and a point ''P'' not on ''l'', right- and left- limiting parallels to ''l'' through ''P'' converge to ''l'' at ''ideal points''. Unlike the projective case, ideal points form a boundary, not a submanifold. So, these lines do not intersect at an ideal point and such points, although well-defined, do not belong to the hyperbolic space itself. The ideal points together form the Cayley absolute or boundary of a hyperbolic geometry. For instance, the unit circle forms the Cayley absolute of the Poincaré disk model and the Klein disk model. While the real line forms the Cayley absolute of the Poincaré half-plane model . Pasch's axiom and the exterior angle theorem still hold for an omega triangle, defined by two points in hyperbolic space and an omega point. Properties * The hyperbolic distance between an ideal point an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercycle (geometry)
In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line (its axis). Given a straight line and a point not on , one can construct a hypercycle by taking all points on the same side of as , with perpendicular distance to equal to that of . The line is called the ''axis'', ''center'', or ''base line'' of the hypercycle. The lines perpendicular to , which are also perpendicular to the hypercycle, are called the '' normals'' of the hypercycle. The segments of the normals between and the hypercycle are called the ''radii''. Their common length is called the ''distance'' or ''radius'' of the hypercycle. The hypercycles through a given point that share a tangent through that point converge towards a horocycle as their distances go towards infinity. Properties similar to those of Euclidean lines Hypercycles in hyperbolic geometry have some properties similar to those of lines in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lambert Quadrilateral
In geometry, a Lambert quadrilateral (also known as Ibn al-Haytham–Lambert quadrilateral), is a quadrilateral in which three of its angles are right angles. Historically, the fourth angle of a Lambert quadrilateral was of considerable interest since if it could be shown to be a right angle, then the Euclidean parallel postulate could be proved as a theorem. It is now known that the type of the fourth angle depends upon the geometry in which the quadrilateral exists. In hyperbolic geometry the fourth angle is acute, in Euclidean geometry it is a right angle and in elliptic geometry it is an obtuse angle. A Lambert quadrilateral can be constructed from a Saccheri quadrilateral by joining the midpoints of the base and summit of the Saccheri quadrilateral. This line segment is perpendicular to both the base and summit and so either half of the Saccheri quadrilateral is a Lambert quadrilateral. Lambert quadrilateral in hyperbolic geometry In hyperbolic geometry a Lambert quadril ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Angle
In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin ''angulus rectus''; here ''rectus'' means "upright", referring to the vertical perpendicular to a horizontal base line. Closely related and important geometrical concepts are perpendicular lines, meaning lines that form right angles at their point of intersection, and orthogonality, which is the property of forming right angles, usually applied to vectors. The presence of a right angle in a triangle is the defining factor for right triangles, making the right angle basic to trigonometry. Etymology The meaning of ''right'' in ''right angle'' possibly refers to the Latin adjective ''rectus'' 'erect, straight, upright, perpendicular'. A Greek equivalent is ''orthos'' 'straight; perpendicular' (see orthogonal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rectangles
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram containing a right angle. A rectangle with four sides of equal length is a ''square''. The term " oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ''ABCD'' would be denoted as . The word rectangle comes from the Latin ''rectangulus'', which is a combination of ''rectus'' (as an adjective, right, proper) and ''angulus'' (angle). A crossed rectangle is a crossed (self-intersecting) quadrilateral which consists of two opposite sides of a rectangle along with the two diagonals (therefore only two sides are parallel). It is a special case of an antiparallelogram, and its angles are not right angles and not all equal, though opposite angles are equal. Other geometries, such as spherical, elliptic, and hype ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Coordinates
In mathematics, hyperbolic coordinates are a method of locating points in quadrant I of the Cartesian plane :\ = Q. Hyperbolic coordinates take values in the hyperbolic plane defined as: :HP = \. These coordinates in ''HP'' are useful for studying logarithmic comparisons of direct proportion in ''Q'' and measuring deviations from direct proportion. For (x,y) in Q take :u = \ln \sqrt and :v = \sqrt. The parameter ''u'' is the hyperbolic angle to (''x, y'') and ''v'' is the geometric mean of ''x'' and ''y''. The inverse mapping is :x = v e^u ,\quad y = v e^. The function Q \rarr HP is a continuous mapping, but not an analytic function. Alternative quadrant metric Since ''HP'' carries the metric space structure of the Poincaré half-plane model of hyperbolic geometry, the bijective correspondence Q \leftrightarrow HP brings this structure to ''Q''. It can be grasped using the notion of hyperbolic motions. Since geodesics in ''HP'' are semicircles with centers on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |