|
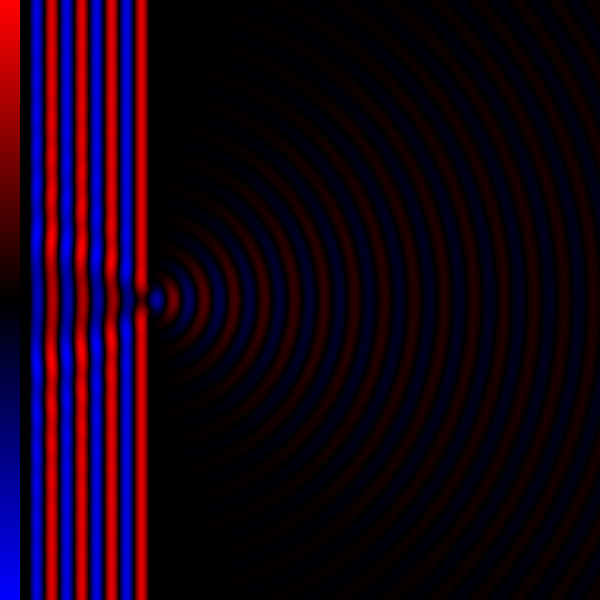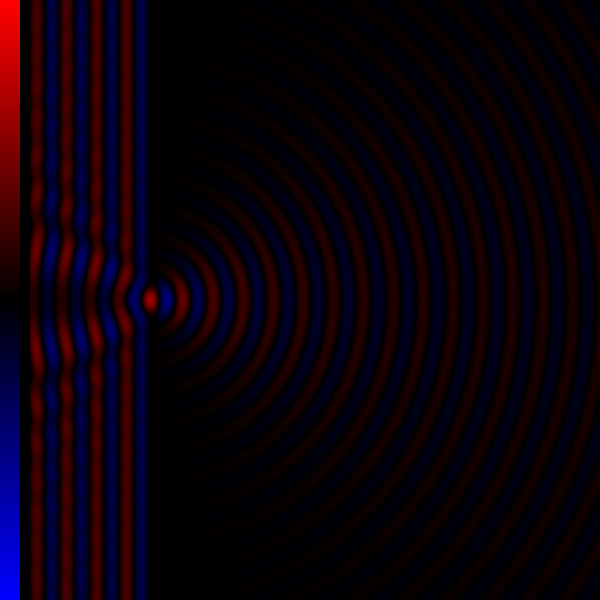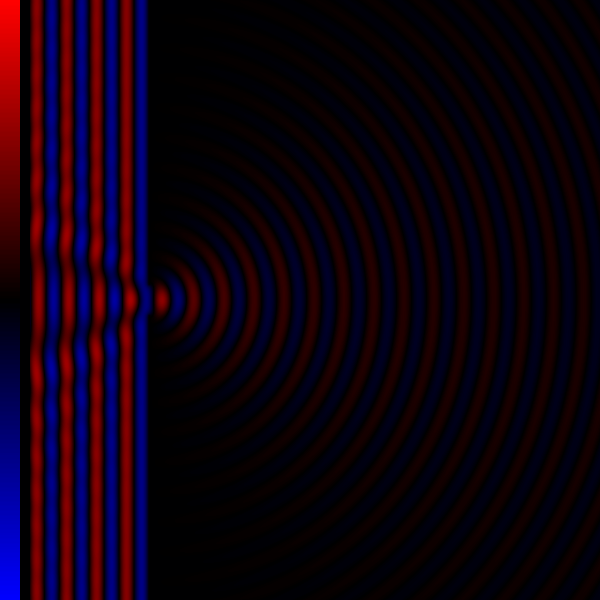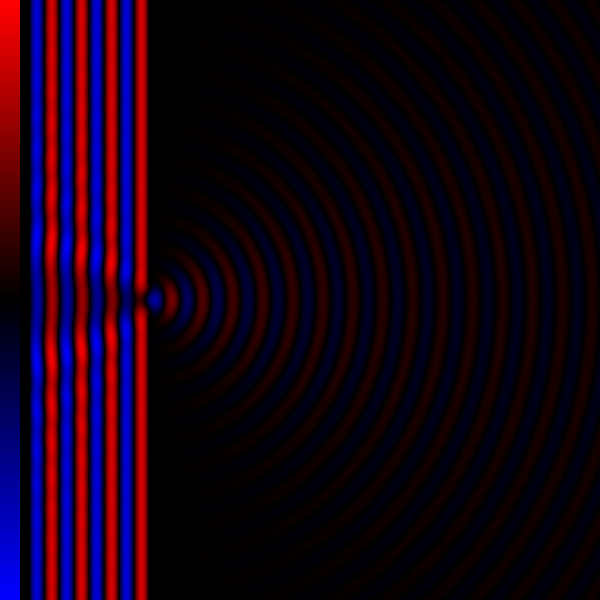
Contrast Transfer Function
The contrast transfer function (CTF) mathematically describes how aberrations in a transmission electron microscope (TEM) modify the image of a sample.Spence, John C. H. (1988 2nd ed) ''Experimental high-resolution electron microscopy'' (Oxford U. Press, NY) .Ludwig Reimer (1997 4th ed) ''Transmission electron microscopy: Physics of image formation and microanalysis'' (Springer, BerlinpreviewEarl J. Kirkland (1998) ''Advanced computing in electron microscopy'' (Plenum Press, NY). This contrast transfer function (CTF) sets the resolution of high-resolution transmission electron microscopy (HRTEM), also known as phase contrast TEM. By considering the recorded image as a CTF-degraded true object, describing the CTF allows the true object to be reverse-engineered. This is typically denoted CTF-correction, and is vital to obtain high resolution structures in three-dimensional electron microscopy, especially electron cryo-microscopy. Its equivalent in light-based optics is the optical tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Aberration
In optics, spherical aberration (SA) is a type of aberration found in optical systems that have elements with spherical surfaces. This phenomenon commonly affects lenses and curved mirrors, as these components are often shaped in a spherical manner for ease of manufacturing. Light rays that strike a spherical surface off-centre are refracted or reflected more or less than those that strike close to the centre. This deviation reduces the quality of images produced by optical systems. The effect of spherical aberration was first identified in the 11th century by Ibn al-Haytham who discussed it in his work Kitāb al-Manāẓir. Overview A spherical lens has an aplanatic point (i.e., no spherical aberration) only at a lateral distance from the optical axis that equals the radius of the spherical surface divided by the index of refraction of the lens material. Spherical aberration makes the focus of telescopes and other instruments less than ideal. This is an important effect, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transmission Electron Microscopy
Transmission electron microscopy (TEM) is a microscopy technique in which a beam of electrons is transmitted through a specimen to form an image. The specimen is most often an ultrathin section less than 100 nm thick or a suspension on a grid. An image is formed from the interaction of the electrons with the sample as the beam is transmitted through the specimen. The image is then magnified and focused onto an imaging device, such as a fluorescent screen, a layer of photographic film, or a detector such as a scintillator attached to a charge-coupled device or a direct electron detector. Transmission electron microscopes are capable of imaging at a significantly higher resolution than light microscopes, owing to the smaller de Broglie wavelength of electrons. This enables the instrument to capture fine detail—even as small as a single column of atoms, which is thousands of times smaller than a resolvable object seen in a light microscope. Transmission electron micr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Point Spread Function
The point spread function (PSF) describes the response of a focused optical imaging system to a point source or point object. A more general term for the PSF is the system's impulse response; the PSF is the impulse response or impulse response function (IRF) of a focused optical imaging system. The PSF in many contexts can be thought of as the shapeless blob in an image that should represent a single point object. We can consider this as a spatial impulse response function. In functional terms, it is the spatial domain version (i.e., the inverse Fourier transform) of the Optical transfer function, optical transfer function (OTF) of an imaging system. It is a useful concept in Fourier optics, astronomy, astronomical imaging, medical imaging, electron microscope, electron microscopy and other imaging techniques such as dimension, 3D microscopy (like in confocal laser scanning microscopy) and fluorescence microscopy. The degree of spreading (blurring) in the image of a point ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Transfer Function
The optical transfer function (OTF) of an optical system such as a camera, microscope, human eye, or image projector, projector is a scale-dependent description of their imaging contrast. Its magnitude is the image contrast of the Sine and cosine, harmonic intensity pattern, 1 + \cos(2\pi \nu \cdot x), as a function of the spatial frequency, \nu, while its Argument (complex analysis), complex argument indicates a phase shift in the periodic pattern. The optical transfer function is used by optical engineers to describe how the optics project light from the object or scene onto a photographic film, Image sensor, detector array, retina, screen, or simply the next item in the optical transmission chain. Formally, the optical transfer function is defined as the Fourier transform of the point spread function (PSF, that is, the impulse response of the optics, the image of a point source). As a Fourier transform, the OTF is generally complex-valued; however, it is real-valued in the comm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Airy Disk
In optics, the Airy disk (or Airy disc) and Airy pattern are descriptions of the best-focus (optics), focused Point source#Light, spot of light that a perfect lens (optics), lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy. The diffraction pattern resulting from a uniformly illuminated, circular aperture has a bright circle of confusion, central region, known as the Airy disk, which together with the series of concentric objects, concentric rings around is called the Airy pattern. Both are named after George Biddell Airy. The disk and rings phenomenon had been known prior to Airy; John Herschel described the appearance of a bright star seen through a telescope under high magnification for an 1828 article on light for the ''Encyclopedia Metropolitana'': Airy wrote the first full theoretical treatment explaining the phenomenon (his 1835 "On the Diffraction of an Object-glass with Circul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Theory Of Diffraction
The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice are atomic crystal structures or nanometer-scale multi-layers or self-arranged systems. In a wider sense, similar treatment is related to the interaction of light with optical band-gap materials or related wave problems in acoustics. The sections below deal with dynamical diffraction of X-rays. Principle The dynamical theory of diffraction considers the wave field in the periodic potential of the crystal and takes into account all multiple scattering effects. Unlike the kinematic theory of diffraction which describes the approximate position of Bragg or Laue diffraction peaks in reciprocal space, dynamical theory corrects for refraction, shape and width of the peaks, extinction and interference effects. Graphical representations are described in dispersion surfaces around reciprocal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffraction Formalism
Diffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations. General diffraction Because diffraction is the result of addition of all waves (of given wavelength) along all unobstructed paths, the usual procedure is to consider the contribution of an infinitesimally small neighborhood around a certain path (this contribution is usually called a wavelet) and then integrate over all paths (= add all wavelets) from the source to the detector (or given point on a screen). Thus in order to determine the pattern produced by diffraction, the phase and the amplitude of each of the wavelets is calculated. That is, at each point in space we must determine the distance to each of the simple sources on the incoming wavefront. If th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurence D
Laurence is in modern use as an English masculine and a French feminine given name. The modern English masculine name is a variant of Lawrence and originates from a French form of the Latin ''Laurentius'', a name meaning "man from Laurentum". The French feminine name Laurence is derived from the same source and is used in French-speaking countries as a form of the masculine '' Laurent''. The name was used in the Middle Ages for both males and females in honor of Saint Laurence, one of the seven deacons of Rome. In England, it was also given in reference to Saint Laurence of Canterbury. In other languages: Lorenzo (Italian, Spanish), Lorenz ( German). In Ireland, Laurence has traditionally been used as an Anglicization of the Irish masculine name Lorcan or Lorcán. Usage Laurence, used as a spelling variant of the more popular Lawrence, was in regular use for boys in the Anglosphere since the medieval era. It was most popular for boys in English-speaking countries during ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CTF Modified By Spatial And Temporal Envelope Functions
CTF may refer to: Organizations and associations * Cambridge Theological Federation, association of colleges etc. in Cambridge, England * Canadian Taxpayers Federation * Canadian Teachers' Federation * Child Trust Fund, a UK child savings scheme * Children's Tumor Foundation, United States, supports those with neurofibromatosis/schwannomatosis * Clean Technology Fund * Cyprus Tennis Federation * Chow Tai Fook, Hong Kong based conglomerate Science and technology * Capture the flag (cybersecurity), an educational exercise in computer security * Charge trap flash * Chlorine trifluoride, a highly corrosive chemical * Collaborative Translation Framework, a platform designed by Microsoft to improve machine translation through (possibly crowdsourced) user contributions * Computer to film, an imaging technology used in lithographic printing * Contrast threshold function, in physiological imaging * Contrast transfer function, in general imaging * Controlled thermonuclear fusio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulus Squared
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 (caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is '' quadratic''. The square of an integer may also be called a ''square number'' or a ''perfect square''. In algebra, the operation of squaring is often generalized to polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial is the quadratic polynomial . One of the important properties of squaring, for numbers as well as in many other mathematical systems, is that (for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |