|
Conformally Flat Manifold
A (pseudo-) Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation. In practice, the metric g of the manifold M has to be conformal to the flat metric \eta, i.e., the geodesics maintain in all points of M the angles by moving from one to the other, as well as keeping the null geodesics unchanged, that means exists a function \lambda(x) such that g(x) = \lambda^2(x)\, \eta, where \lambda(x) is known as the conformal factor and x is a point on the manifold. More formally, let (M,g) be a pseudo-Riemannian manifold. Then (M,g) is conformally flat if for each point x in M, there exists a neighborhood U of x and a smooth function f defined on U such that (U,e^ g) is flat (i.e. the curvature of e^ g vanishes on U). The function f need not be defined on all of M. Some authors use the definition of locally conformally flat when referred to just some point x on M and reserve the definition of ''conformally f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map
In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths. More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in U if it preserves angles between directed curves through u_0, as well as preserving orientation. Conformal maps preserve both angles and the shapes of infinitesimally small figures, but not necessarily their size or curvature. The conformal property may be described in terms of the Jacobian derivative matrix of a coordinate transformation. The transformation is conformal whenever the Jacobian at each point is a positive scalar times a rotation matrix (orthogonal with determinant one). Some authors define conformality to include orientation-reversing mappings whose Jacobians can be written as any scalar times any orthogonal matrix. For mappings in two dimensions, the (orientation-preserving) conformal mappings are precisely the locally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
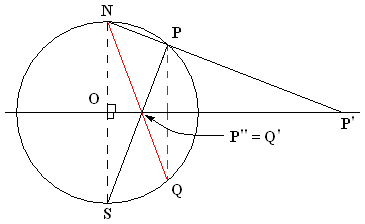
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric (distance preserving) nor equiareal (area preserving). The stereographic projection gives a way to represent a sphere by a plane. The metric induced by the inverse stereographic projection from the plane to the sphere defines a geodesic distance between points in the plane equal to the spherical distance between the spherical points they represent. A two-dimensional coordinate system on the stereo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Geometry
In mathematics, conformal geometry is the study of the set of angle-preserving ( conformal) transformations on a space. In a real two dimensional space, conformal geometry is precisely the geometry of Riemann surfaces. In space higher than two dimensions, conformal geometry may refer either to the study of conformal transformations of what are called "flat spaces" (such as Euclidean spaces or spheres), or to the study of conformal manifolds which are Riemannian or pseudo-Riemannian manifolds with a class of metrics that are defined up to scale. Study of the flat structures is sometimes termed Möbius geometry, and is a type of Klein geometry. Conformal manifolds A conformal manifold is a pseudo-Riemannian manifold equipped with an equivalence class of metric tensors, in which two metrics ''g'' and ''h'' are equivalent if and only if :h = \lambda^2 g , where ''λ'' is a real-valued smooth function defined on the manifold and is called the conformal factor. An equivalence clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yamabe Problem
The Yamabe problem refers to a conjecture in the mathematical field of differential geometry, which was resolved in the 1980s. It is a statement about the scalar curvature of Riemannian manifolds: By computing a formula for how the scalar curvature of relates to that of , this statement can be rephrased in the following form: The mathematician Hidehiko Yamabe, in the paper , gave the above statements as theorems and provided a proof; however, discovered an error in his proof. The problem of understanding whether the above statements are true or false became known as the Yamabe problem. The combined work of Yamabe, Trudinger, Thierry Aubin, and Richard Schoen provided an affirmative resolution to the problem in 1984. It is now regarded as a classic problem in geometric analysis, with the proof requiring new methods in the fields of differential geometry and partial differential equations. A decisive point in Schoen's ultimate resolution of the problem was an application of the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Geometry
In mathematics, conformal geometry is the study of the set of angle-preserving ( conformal) transformations on a space. In a real two dimensional space, conformal geometry is precisely the geometry of Riemann surfaces. In space higher than two dimensions, conformal geometry may refer either to the study of conformal transformations of what are called "flat spaces" (such as Euclidean spaces or spheres), or to the study of conformal manifolds which are Riemannian or pseudo-Riemannian manifolds with a class of metrics that are defined up to scale. Study of the flat structures is sometimes termed Möbius geometry, and is a type of Klein geometry. Conformal manifolds A conformal manifold is a pseudo-Riemannian manifold equipped with an equivalence class of metric tensors, in which two metrics ''g'' and ''h'' are equivalent if and only if :h = \lambda^2 g , where ''λ'' is a real-valued smooth function defined on the manifold and is called the conformal factor. An equivalence clas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weyl–Schouten Theorem
In the mathematical field of differential geometry, the existence of isothermal coordinates for a ( pseudo-)Riemannian metric is often of interest. In the case of a metric on a two-dimensional space, the existence of isothermal coordinates is unconditional. For higher-dimensional spaces, the Weyl–Schouten theorem (named after Hermann Weyl and Jan Arnoldus Schouten) characterizes the existence of isothermal coordinates by certain equations to be satisfied by the Riemann curvature tensor of the metric. Existence of isothermal coordinates is also called conformal flatness, although some authors refer to it instead as ''local conformal flatness''; for those authors, conformal flatness refers to a more restrictive condition. Theorem In terms of the Riemann curvature tensor, the Ricci tensor, and the scalar curvature, the Weyl tensor of a pseudo-Riemannian metric of dimension is given by :W_=R_-\frac+\frac(g_g_-g_g_). The Schouten tensor is defined via the Ricci and scalar curvature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kruskal–Szekeres Coordinates
In general relativity, Kruskal–Szekeres coordinates, named after Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole. These coordinates have the advantage that they cover the entire spacetime manifold of the maximally extended Schwarzschild solution and are well-behaved everywhere outside the physical singularity. There is no misleading coordinate singularity at the horizon. The Kruskal–Szekeres coordinates also apply to space-time around a spherical object, but in that case do not give a description of space-time inside the radius of the object. Space-time in a region where a star is collapsing into a black hole is approximated by the Kruskal–Szekeres coordinates (or by the Schwarzschild coordinates). The surface of the star remains outside the event horizon in the Schwarzschild coordinates, but crosses it in the Kruskal–Szekeres coordinates. (In any "black hole" which we observe, we see it at a time when its matt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
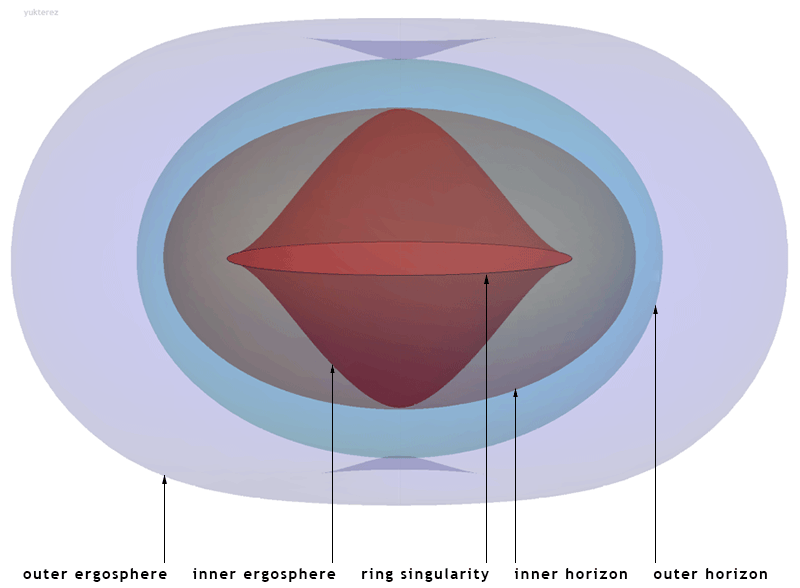
Kerr Spacetime
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find. Overview The Kerr metric is a generalization to a rotating body of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically symmetric, and non-rotating body. The corresponding solution for a ''charged'', spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, ''rotating'' black hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr.Melia, Fulvio (2009). "Cracking the Einstein code: relativity and the birth of black h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Friedmann–Lemaître–Robertson–Walker Metric
The Friedmann–Lemaître–Robertson–Walker (FLRW; ) metric is a metric based on the exact solution of Einstein's field equations of general relativity; it describes a homogeneous, isotropic, expanding (or otherwise, contracting) universe that is path-connected, but not necessarily simply connected. The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists – Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker – are customarily grouped as Friedmann or Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL). This model is sometimes called the ''Standard Model'' of modern cosmology, although such a description is also associated with the further developed Lambda-CDM model. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-sphere
In mathematics, an -sphere or a hypersphere is a topological space that is homeomorphic to a ''standard'' -''sphere'', which is the set of points in -dimensional Euclidean space that are situated at a constant distance from a fixed point, called the ''center''. It is the generalization of an ordinary sphere in the ordinary three-dimensional space. The "radius" of a sphere is the constant distance of its points to the center. When the sphere has unit radius, it is usual to call it the unit -sphere or simply the -sphere for brevity. In terms of the standard norm, the -sphere is defined as : S^n = \left\ , and an -sphere of radius can be defined as : S^n(r) = \left\ . The dimension of -sphere is , and must not be confused with the dimension of the Euclidean space in which it is naturally embedded. An -sphere is the surface or boundary of an -dimensional ball. In particular: *the pair of points at the ends of a (one-dimensional) line segment is a 0-sphere, *a circle, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simply Connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the space) into any other such path while preserving the two endpoints in question. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit circle and closed unit disk in the Euclidean plane respectively. An equivalent formulation is this: X is simply connected if and only if it is path-connected, and when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |