|
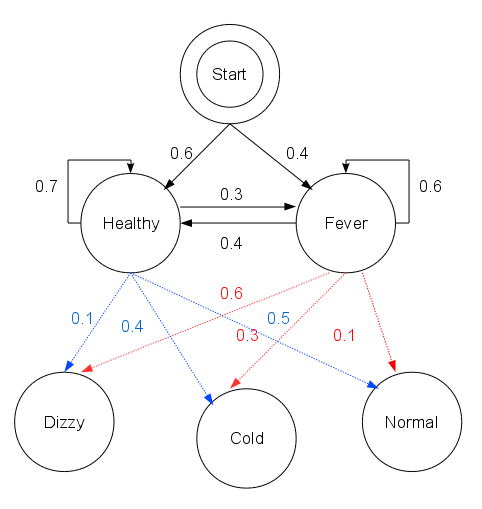
Conditional Random Field
Conditional random fields (CRFs) are a class of statistical modeling methods often applied in pattern recognition and machine learning and used for structured prediction. Whereas a classifier predicts a label for a single sample without considering "neighbouring" samples, a CRF can take context into account. To do so, the predictions are modelled as a graphical model, which represents the presence of dependencies between the predictions. The kind of graph used depends on the application. For example, in natural language processing, "linear chain" CRFs are popular, for which each prediction is dependent only on its immediate neighbours. In image processing, the graph typically connects locations to nearby and/or similar locations to enforce that they receive similar predictions. Other examples where CRFs are used are: labeling or parsing of sequential data for natural language processing or biological sequences, part-of-speech tagging, shallow parsing, named entity recogn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discriminative Model
Discriminative models, also referred to as conditional models, are a class of models frequently used for classification. They are typically used to solve binary classification problems, i.e. assign labels, such as pass/fail, win/lose, alive/dead or healthy/sick, to existing datapoints. Types of discriminative models include logistic regression (LR), conditional random fields (CRFs), decision trees among many others. Generative model approaches which uses a joint probability distribution instead, include naive Bayes classifiers, Gaussian mixture models, variational autoencoders, generative adversarial networks and others. Definition Unlike generative modelling, which studies the joint probability P(x,y), discriminative modeling studies the P(y, x) or maps the given unobserved variable (target) x to a class label y dependent on the observed variables (training samples). For example, in object recognition, x is likely to be a vector of raw pixels (or features extracted from the ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Model
A statistical model is a mathematical model that embodies a set of statistical assumptions concerning the generation of Sample (statistics), sample data (and similar data from a larger Statistical population, population). A statistical model represents, often in considerably idealized form, the Data generating process, data-generating process. When referring specifically to probability, probabilities, the corresponding term is probabilistic model. All Statistical hypothesis testing, statistical hypothesis tests and all Estimator, statistical estimators are derived via statistical models. More generally, statistical models are part of the foundation of statistical inference. A statistical model is usually specified as a mathematical relationship between one or more random variables and other non-random variables. As such, a statistical model is "a formal representation of a theory" (Herman J. Adèr, Herman Adèr quoting Kenneth A. Bollen, Kenneth Bollen). Introduction Informally, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming Relaxation
In mathematics, the relaxation of a (mixed) integer linear program is the problem that arises by removing the integrality constraint of each variable. For example, in a 0–1 integer program, all constraints are of the form :x_i\in\. The relaxation of the original integer program instead uses a collection of linear constraints :0 \le x_i \le 1. The resulting relaxation is a linear program, hence the name. This relaxation technique transforms an NP-hard optimization problem (integer programming) into a related problem that is solvable in polynomial time (linear programming); the solution to the relaxed linear program can be used to gain information about the solution to the original integer program. Example Consider the set cover problem, the linear programming relaxation of which was first considered by Lovász in 1975. In this problem, one is given as input a family of sets ''F'' = ; the task is to find a subfamily, with as few sets as possible, having the same union as ''F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Belief Propagation
Belief propagation, also known as sum–product message passing, is a message-passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node (or variable), conditional on any observed nodes (or variables). Belief propagation is commonly used in artificial intelligence and information theory, and has demonstrated empirical success in numerous applications, including low-density parity-check codes, turbo codes, free energy approximation, and satisfiability. The algorithm was first proposed by Judea Pearl in 1982, who formulated it as an exact inference algorithm on trees, later extended to polytrees. While the algorithm is not exact on general graphs, it has been shown to be a useful approximate algorithm. Motivation Given a finite set of discrete random variables X_1, \ldots, X_n with joint probability mass function p, a common task is to compute ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Submodular Function
In mathematics, a submodular set function (also known as a submodular function) is a set function that, informally, describes the relationship between a set of inputs and an output, where adding more of one input has a decreasing additional benefit ( diminishing returns). The natural diminishing returns property which makes them suitable for many applications, including approximation algorithms, game theory (as functions modeling user preferences) and electrical networks. Recently, submodular functions have also found utility in several real world problems in machine learning and artificial intelligence, including automatic summarization, multi-document summarization, feature selection, active learning, sensor placement, image collection summarization and many other domains. Definition If \Omega is a finite set, a submodular function is a set function f:2^\rightarrow \mathbb, where 2^\Omega denotes the power set of \Omega, which satisfies one of the following equivalent conditi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Viterbi Algorithm
The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM). The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal. His ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphical Model
A graphical model or probabilistic graphical model (PGM) or structured probabilistic model is a probabilistic model for which a graph expresses the conditional dependence structure between random variables. Graphical models are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning. Types of graphical models Generally, probabilistic graphical models use a graph-based representation as the foundation for encoding a distribution over a multi-dimensional space and a graph that is a compact or factorized representation of a set of independences that hold in the specific distribution. Two branches of graphical representations of distributions are commonly used, namely, Bayesian networks and Markov random fields. Both families encompass the properties of factorization and independences, but they differ in the set of independences they can encode and the factorization of the distribution that they induce. Undirected Graphical Model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neighbourhood (graph Theory)
In graph theory, an adjacent vertex of a vertex (graph theory), vertex in a Graph (discrete mathematics), graph is a vertex that is connected to by an edge (graph theory), edge. The neighbourhood of a vertex in a graph is the subgraph of induced subgraph, induced by all vertices adjacent to , i.e., the graph composed of the vertices adjacent to and all edges connecting vertices adjacent to . The neighbourhood is often denoted or (when the graph is unambiguous) . The same neighbourhood notation may also be used to refer to sets of adjacent vertices rather than the corresponding induced subgraphs. The neighbourhood described above does not include itself, and is more specifically the open neighbourhood of ; it is also possible to define a neighbourhood in which itself is included, called the closed neighbourhood and denoted by . When stated without any qualification, a neighbourhood is assumed to be open. Neighbourhoods may be used to represent graphs in computer algori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process, which means that its future evolution is independent of its history. It is named after the Russian mathematician Andrey Markov. The term strong Markov property is similar to the Markov property, except that the meaning of "present" is defined in terms of a random variable known as a stopping time. The term Markov assumption is used to describe a model where the Markov property is assumed to hold, such as a hidden Markov model. A Markov random field extends this property to two or more dimensions or to random variables defined for an interconnected network of items. An example of a model for such a field is the Ising model. A discrete-time stochastic process satisfying the Markov property is known as a Markov chain. Introduction A stochastic process has the Markov property if the conditional probability distribution of future states of the process (cond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrew McCallum
Andrew McCallum is a professor in the computer science department at University of Massachusetts Amherst. His primary specialties are in machine learning, natural language processing, information extraction, information integration, and social network analysis. Career McCallum graduated summa cum laude from Dartmouth College in 1989. He completed his Ph.D. at University of Rochester in 1995 under the supervision of Dana H. Ballard. He was then a postdoctoral fellow, working with Sebastian Thrun and Tom M. Mitchell at Carnegie Mellon University. From 1998 to 2000 he was a Research Scientist and Research Coordinator at Justsystem Pittsburgh Research Center. From 2000 to 2002 was Vice President of Research and Development at WhizBang Labs, and Director of its Pittsburgh office. Since 2002, he worked as a professor of computer science at the University of Massachusetts Amherst. In 2020, he also joined Google as a part-time research scientist. He was elected as a fellow of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |