|
Cluster Expansion
In statistical mechanics, the cluster expansion (also called the high temperature expansion or hopping expansion) is a power series expansion of the partition function of a statistical field theory around a model that is a union of non-interacting 0-dimensional field theories. Cluster expansions originated in the work of . Unlike the usual perturbation expansion which usually leads to a divergent asymptotic series, the cluster expansion may converge within a non-trivial region, in particular when the interaction is small and short-ranged. Classical case General theory In statistical mechanics, the properties of a system of noninteracting particles are described using the partition function. For N noninteracting particles, the system is described by the Hamiltonian : \big. H_0=\sum_i^N \frac, and the partition function can be calculated (for the classical case) as :\big. Z_0 =\frac\int \prod_i d\vec_i\;d\vec_i \exp\left\ =\frac\left( \frac \right)^. From the partition functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
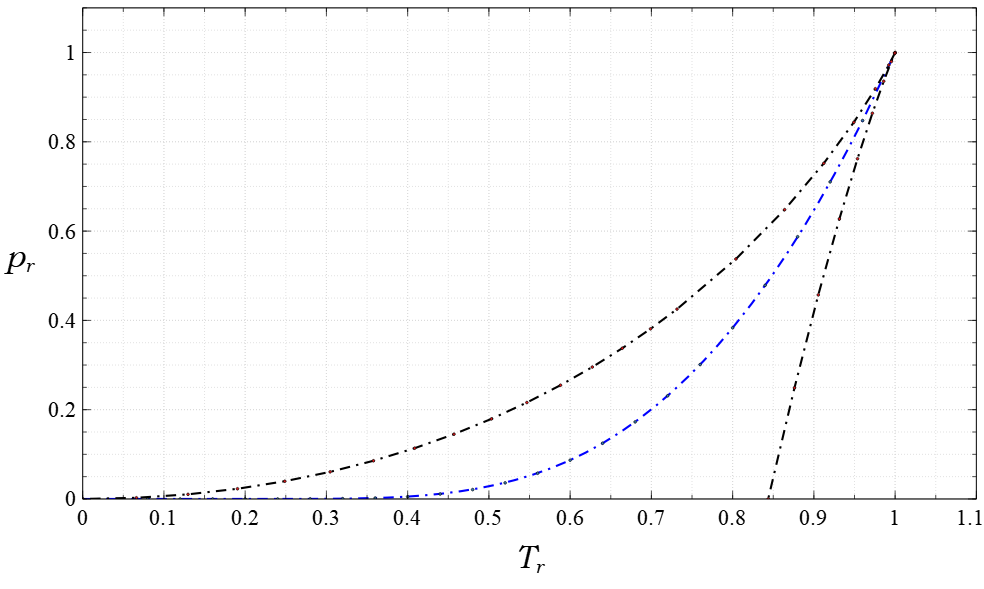
Equation Of State
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predict ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Butterworth-Heinemann
Butterworth–Heinemann is a British publishing company specialised in professional information and learning materials for higher education and professional training, in printed and electronic forms. It was formed in 1990 by the merger of Heinemann Professional Publishing and Butterworths Scientific, both subsidiaries of Reed International. With its earlier constituent companies, the founding dates back to 1923. It has publishing units in Oxford (UK) and Waltham, Massachusetts (United States). As of 2006, it is an imprint of Elsevier. See also *LexisNexis Butterworths LexisNexis is a part of the RELX corporation that sells data analytics products and various databases that are accessed through online portals, including portals for computer-assisted legal research (CALR), newspaper search, and consumer informa ... References External links * Book publishing companies of the United Kingdom Elsevier imprints {{publish-corp-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Course Of Theoretical Physics
The ''Course of Theoretical Physics'' is a ten-volume series of books covering theoretical physics that was initiated by Lev Landau and written in collaboration with his student Evgeny Lifshitz starting in the late 1930s. It is said that Landau composed much of the series in his head while in an NKVD prison in 1938–1939. However, almost all of the actual writing of the early volumes was done by Lifshitz, giving rise to the witticism, "not a word of Landau and not a thought of Lifshitz". The first eight volumes were finished in the 1950s, written in Russian and translated into English in the late 1950s by John Stewart Bell, together with John Bradbury Sykes, M. J. Kearsley, and W. H. Reid. The last two volumes were written in the early 1980s. Vladimir Berestetskii and Lev Pitaevskii also contributed to the series. The series is often referred to as "Landau and Lifshitz", "Landafshitz" (Russian: "Ландафшиц"), or "Lanlifshitz" (Russian: "Ланлифшиц") in informal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by Henry VIII of England, King Henry VIII in 1534, it is the oldest university press A university press is an academic publishing house specializing in monographs and scholarly journals. Most are nonprofit organizations and an integral component of a large research university. They publish work that has been reviewed by schola ... in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 Country, countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Van Der Waals Equation
In chemistry and thermodynamics, the Van der Waals equation (or Van der Waals equation of state) is an equation of state which extends the ideal gas law to include the effects of interaction between molecules of a gas, as well as accounting for the finite size of the molecules. The ideal gas law treats gas molecules as point particles that interact with their containers but not each other, meaning they neither take up space nor change kinetic energy during collisions (i.e. all collisions are perfectly elastic). The ideal gas law states that the volume ''V'' occupied by ''n'' moles of any gas has a pressure ''P'' at temperature ''T'' given by the following relationship, where ''R'' is the gas constant: :PV=nRT To account for the volume occupied by real gas molecules, the Van der Waals equation replaces V/n in the ideal gas law with (V_m-b), where ''Vm'' is the molar volume of the gas and ''b'' is the volume occupied by the molecules of one mole: :P(V_m - b)=R T The second m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Coefficients
Virial coefficients B_i appear as coefficients in the virial expansion of the pressure of a many-particle system in powers of the density, providing systematic corrections to the ideal gas law. They are characteristic of the interaction potential between the particles and in general depend on the temperature. The second virial coefficient B_2 depends only on the pair interaction between the particles, the third (B_3) depends on 2- and non-additive 3-body interactions, and so on. Derivation The first step in obtaining a closed expression for virial coefficients is a cluster expansion of the grand canonical partition function : \Xi = \sum_ = e^ Here p is the pressure, V is the volume of the vessel containing the particles, k_B is Boltzmann's constant, T is the absolute temperature, \lambda =\exp mu/(k_BT) is the fugacity, with \mu the chemical potential. The quantity Q_n is the canonical partition function of a subsystem of n particles: : Q_n = \operatorname e^ Here H(1,2,\ld ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Virial Equation
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predict ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mayer Function
The Mayer f-function is an auxiliary function that often appears in the series expansion of thermodynamic quantities related to classical many-particle systems.Donald Allan McQuarrie, ''Statistical Mechanics'' (HarperCollins, 1976), page 228 It is named after chemist and physicist Joseph Edward Mayer. Definition Consider a system of classical particles interacting through a pair-wise potential :V(\mathbf,\mathbf) where the bold labels \mathbf and \mathbf denote the continuous degrees of freedom associated with the particles, e.g., :\mathbf=\mathbf_i for spherically symmetric particles and :\mathbf=(\mathbf_i,\Omega_i) for rigid non-spherical particles where \mathbf denotes position and \Omega the orientation parametrized e.g. by Euler angles. The Mayer f-function is then defined as :f(\mathbf,\mathbf)=e^-1 where \beta=(k_T)^ the inverse absolute temperature in units of (Temperature times the Boltzmann constant k_)−1 . See also *Virial coefficient *Cluster expansion *Excluded vol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Series Expansion
In mathematics, a power series (in one variable) is an infinite series of the form \sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots where ''an'' represents the coefficient of the ''n''th term and ''c'' is a constant. Power series are useful in mathematical analysis, where they arise as Taylor series of infinitely differentiable functions. In fact, Borel's theorem implies that every power series is the Taylor series of some smooth function. In many situations, ''c'' (the ''center'' of the series) is equal to zero, for instance when considering a Maclaurin series. In such cases, the power series takes the simpler form \sum_^\infty a_n x^n = a_0 + a_1 x + a_2 x^2 + \dots. Beyond their role in mathematical analysis, power series also occur in combinatorics as generating functions (a kind of formal power series) and in electronic engineering (under the name of the Z-transform). The familiar decimal notation for real numbers can also be viewed as an ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Configuration Integral
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless. Each partition function is constructed to represent a particular statistical ensemble (which, in turn, corresponds to a particular free energy). The most common statistical ensembles have named partition functions. The canonical partition function applies to a canonical ensemble, in which the system is allowed to exchange heat with the environment at fixed temperature, volume, and number of particles. The grand canonical partition function applies to a grand canonical ensemble, in which the system can exchange both heat and pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
