|
Cauchy's Theorem (geometry)
Cauchy's theorem is a theorem in geometry, named after Augustin-Louis Cauchy, Augustin Cauchy. It states that convex polytopes in three dimensions with congruence (geometry), congruent corresponding faces must be congruent to each other. That is, any Net (polyhedron), polyhedral net formed by unfolding the faces of the polyhedron onto a flat surface, together with gluing instructions describing which faces should be connected to each other, uniquely determines the shape of the original polyhedron. For instance, if six squares are connected in the pattern of a cube, then they must form a cube: there is no convex polyhedron with six square faces connected in the same way that does not have the same shape. This is a fundamental result in rigidity theory (structural), rigidity theory: one consequence of the theorem is that, if one makes a physical model of a convex polyhedron by connecting together rigid plates for each of the polyhedron faces with flexible hinges along the polyhedron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
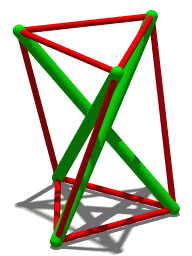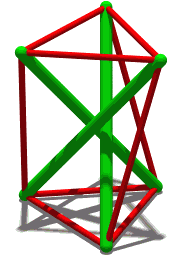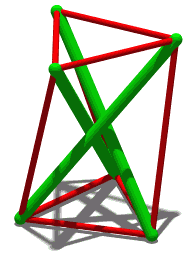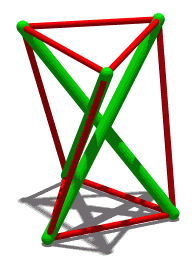
Flexible Polyhedra
In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex (this is also true in higher dimensions). Examples The first examples of flexible polyhedra, now called Bricard octahedra, were discovered by . They are self-intersecting surfaces isometric to an octahedron. The first example of a flexible non-self-intersecting surface in \mathbb^3, the Connelly sphere, was discovered by . Steffen's polyhedron is another non-self-intersecting flexible polyhedron derived from Bricard's octahedra. Bellows conjecture In the late 1970s Connelly and D. Sullivan formulated the bellows conjecture stating that the volume of a flexible polyhedron is invariant under flexing. This conjecture was proved for polyhedra homeomorphic to a sphere by using elimination theory, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schönhardt Polyhedron
In geometry, a Schönhardt polyhedron is a polyhedron with the same combinatorial structure as a regular octahedron, but with dihedral angles that are non-convex along three disjoint edges. Because it has no interior diagonals, it cannot be triangulated into tetrahedra without adding new vertices. It has the fewest vertices of any polyhedron that cannot be triangulated. It is named after the German mathematician Erich Schönhardt, who described it in 1928, although the artist Karlis Johansons had exhibited a related structure in 1921. One construction for the Schönhardt polyhedron starts with a triangular prism and twists the two equilateral triangle faces of the prism relative to each other, breaking each square face into two triangles separated by a non-convex edge. Some twist angles produce a ''jumping polyhedron'' whose two solid forms share the same face shapes. A 30° twist instead produces a ''shaky polyhedron'', rigid but not infinitesimally rigid, whose edges fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aleksei Pogorelov
Aleksei Vasilyevich Pogorelov (, ; 3 March 1919 – 17 December 2002), was a Soviet mathematician. Specialist in the field of convex and differential geometry, geometric PDEs and elastic shells theory, the author of novel school textbooks on geometry and university textbooks on analytical geometry, on differential geometry, and on the foundations of geometry. Pogorelov's uniqueness theorem and the Alexandrov–Pogorelov theorem are named after him. Biography He was born in Korocha in a peasant family. In 1931, because of the collectivization, the parents of Pogorelov escaped from the village to Kharkiv, where his father become a worker at the construction of the Kharkiv tractor plant. In 1935, Pogorelov won the first prize at the Mathematical Olympiad in Kharkiv State University. After high school graduation in 1937, he entered the mathematical department of the Kharkiv State University. He was the best student at the department. In 1941, after the involvement of the Sovi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stefan Cohn-Vossen
Stefan Cohn-Vossen (28 May 1902 – 25 June 1936) was a mathematician, who was responsible for Cohn-Vossen's inequality and the Cohn-Vossen transformation is also named after him. He proved the first version of the splitting theorem. He was also known for his collaboration with David Hilbert on the 1932 book ''Anschauliche Geometrie'', translated into English as ''Geometry and the Imagination''. He was born in Breslau (then a city in the Kingdom of Prussia; now Wrocław in Poland). He wrote a 1924 doctoral dissertation at the University of Breslau (now the University of Wrocław) under the supervision of Adolf Kneser. He became a professor at the University of Cologne in 1930. He was barred from lecturing in 1933 under Nazi racial legislation, because he was Jewish.. In 1934 he emigrated to the USSR, with some help from Herman Müntz. While there, he taught at Leningrad University. He died in Moscow from pneumonia. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a " straight line". The noun '' geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of havi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), function called a metric or distance function. Metric spaces are a general setting for studying many of the concepts of mathematical analysis and geometry. The most familiar example of a metric space is 3-dimensional Euclidean space with its usual notion of distance. Other well-known examples are a sphere equipped with the angular distance and the hyperbolic plane. A metric may correspond to a Conceptual metaphor , metaphorical, rather than physical, notion of distance: for example, the set of 100-character Unicode strings can be equipped with the Hamming distance, which measures the number of characters that need to be changed to get from one string to another. Since they are very general, metric spaces are a tool used in many different bra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexandrov's Uniqueness Theorem
Alexandrov's theorem on polyhedra is a rigidity theorem in mathematics, describing three-dimensional convex polyhedra in terms of the distances between points on their surfaces. It implies that convex polyhedra with distinct shapes from each other also have distinct metric spaces of surface distances, and it characterizes the metric spaces that come from the surface distances on polyhedra. It is named after Soviet mathematician Aleksandr Danilovich Aleksandrov, who published it in the 1940s. Statement of the theorem The surface of any convex polyhedron in Euclidean space forms a metric space, in which the distance between two points is measured by the length of the shortest path from one point to the other along the surface. Within a single shortest path, distances between pairs of points equal the distances between corresponding points of a line segment of the same length; a path with this property is known as a geodesic. This property of polyhedral surfaces, that every pair of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Dehn
Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States.The story of his travel in 1940 from Norway via Stockholm, Moscow, trans-Siberian train, Vladivostok, Japan to San Francisco is described in Dehn was a student of David Hilbert, and in his habilitation in 1900 Dehn resolved Hilbert's third problem, making him the first to resolve one of Hilbert's problems, Hilbert's well-known 23 problems. Dehn's doctoral students include Ott-Heinrich Keller, Ruth Moufang, and Wilhelm Magnus; he also mentored mathematician Peter Nemenyi and the artists Dorothea Rockburne and Ruth Asawa. Biography Dehn was born to a family of Jewish origin in Hamburg, Imperial Germany. He studied the foundations of geometry with David Hilbert, Hil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Surface
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space. Topological surfaces are sometimes equipped with additional information, such as a Riemannian metric or a complex structure, that connects them to other disciplines within mathematics, such as differential geometry and complex analysis. The various mathematical notions of surface can be used to model surfaces in the physical world. In general In mathematics, a surface is a geometrical shape that resembles a deformed plane. The most familiar examples arise as boundaries of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simply Connected Space
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed into any other such path while preserving the two endpoints in question. Intuitively, this corresponds to a space that has no disjoint parts and no holes that go completely through it, because two paths going around different sides of such a hole cannot be continuously transformed into each other. The fundamental group of a topological space is an indicator of the failure for the space to be simply connected: a path-connected topological space is simply connected if and only if its fundamental group is trivial. Definition and equivalent formulations A topological space X is called if it is path-connected and any loop in X defined by f : S^1 \to X can be contracted to a point: there exists a continuous map F : D^2 \to X such that F restricted to S^1 is f. Here, S^1 and D^2 denotes the unit c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Connelly
Robert Connelly (born July 15, 1942) is a mathematician specializing in discrete geometry and rigidity theory. Connelly received his Ph.D. from University of Michigan in 1969. He is currently a professor at Cornell University. Connelly is best known for discovering embedded flexible polyhedra. One such polyhedron is in the National Museum of American History. His recent interests include tensegrities and the carpenter's rule problem. In 2012 he became a fellow of the American Mathematical Society. Asteroid 4816 Connelly, discovered by Edward Bowell at Lowell Observatory 1981, was named after Robert Connelly. The official was published by the Minor Planet Center The Minor Planet Center (MPC) is the official body for observing and reporting on minor planets under the auspices of the International Astronomical Union (IAU). Founded in 1947, it operates at the Smithsonian Astrophysical Observatory. Funct ... on 18 February 1992 (). Author Connelly has authored or co-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |