|
Box Counting
Box counting is a method of gathering data for analyzing complex patterns by breaking a dataset, object, image, etc. into smaller and smaller pieces, typically "box"-shaped, and analyzing the pieces at each smaller scale. The essence of the process has been compared to zooming in or out using optical or computer based methods to examine how observations of detail change with scale. In box counting, however, rather than changing the magnification or resolution of a lens, the investigator changes the size of the element used to inspect the object or pattern (see Figure 1). Computer based box counting algorithms have been applied to patterns in 1-, 2-, and 3-dimensional spaces. The technique is usually implemented in software for use on patterns extracted from digital media, although the fundamental method can be used to investigate some patterns physically. The technique arose out of and is used in fractal analysis. It also has application in related fields such as lacunarity an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
32 Segment Fractal
3 (three) is a number, numeral and digit. It is the natural number following 2 and preceding 4, and is the smallest odd prime number and the only prime preceding a square number. It has religious or cultural significance in many societies. Evolution of the Arabic digit The use of three lines to denote the number 3 occurred in many writing systems, including some (like Roman and Chinese numerals) that are still in use. That was also the original representation of 3 in the Brahmic (Indian) numerical notation, its earliest forms aligned vertically. However, during the Gupta Empire the sign was modified by the addition of a curve on each line. The Nāgarī script rotated the lines clockwise, so they appeared horizontally, and ended each line with a short downward stroke on the right. In cursive script, the three strokes were eventually connected to form a glyph resembling a with an additional stroke at the bottom: ३. The Indian digits spread to the Caliphate in the 9th ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Box Counting Dimension
A box (plural: boxes) is a container used for the storage or transportation of its contents. Most boxes have flat, parallel, rectangular sides. Boxes can be very small (like a matchbox) or very large (like a shipping box for furniture), and can be used for a variety of purposes from functional to decorative. Boxes may be made of a variety of materials, both durable, such as wood and metal; and non-durable, such as corrugated fiberboard and paperboard. Corrugated metal boxes are commonly used as shipping containers. Most commonly, boxes have flat, parallel, rectangular sides, making them rectangular prisms; but boxes may also have other shapes. Rectangular prisms are often referred to colloquially as "boxes." Boxes may be closed and shut with flaps, doors, or a separate lid. They can be secured shut with adhesives, tapes, or more decorative or elaborately functional mechanisms, such as a catch, clasp or lock. Types Packaging Several types of boxes are used in packaging and s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lacunarity
Lacunarity, from the Latin lacuna, meaning "gap" or "lake", is a specialized term in geometry referring to a measure of how patterns, especially fractals, fill space, where patterns having more or larger gaps generally have higher lacunarity. Beyond being an intuitive measure of gappiness, lacunarity can quantify additional features of patterns such as "rotational invariance" and more generally, heterogeneity. This is illustrated in Figure 1 showing three fractal patterns. When rotated 90°, the first two fairly homogeneous patterns do not appear to change, but the third more heterogeneous figure does change and has correspondingly higher lacunarity. The earliest reference to the term in geometry is usually attributed to Benoit Mandelbrot, who, in 1983 or perhaps as early as 1977, introduced it as, in essence, an adjunct to fractal analysis. Lacunarity analysis is now used to characterize patterns in a wide variety of fields and has application in multifractal analysis in partic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multifractal
A multifractal system is a generalization of a fractal system in which a single exponent (the fractal dimension) is not enough to describe its dynamics; instead, a continuous spectrum of exponents (the so-called singularity spectrum) is needed. Multifractal systems are common in nature. They include the length of coastlines, mountain topography, fully developed turbulence, real-world scenes, heartbeat dynamics, human gait and activity, human brain activity, and natural luminosity time series. Models have been proposed in various contexts ranging from turbulence in fluid dynamics to internet traffic, finance, image modeling, texture synthesis, meteorology, geophysics and more. The origin of multifractality in sequential (time series) data has been attributed to mathematical convergence effects related to the central limit theorem that have as foci of convergence the family of statistical distributions known as the Tweedie exponential dispersion models, as well as the geomet ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski–Bouligand Dimension
450px, Estimating the box-counting dimension of the coast of Great Britain In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set ''S'' in a Euclidean space R''n'', or more generally in a metric space (''X'', ''d''). It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand. To calculate this dimension for a fractal ''S'', imagine this fractal lying on an evenly spaced grid and count how many boxes are required to cover the set. The box-counting dimension is calculated by seeing how this number changes as we make the grid finer by applying a box-counting algorithm. Suppose that ''N''(''ε'') is the number of boxes of side length ''ε'' required to cover the set. Then the box-counting dimension is defined as : \dim_\text(S) := \lim_ \frac . Roughly speaking, this means that the dimension is the exponent ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Dimension
In mathematics, more specifically in fractal geometry, a fractal dimension is a ratio providing a statistical index of complexity comparing how detail in a pattern (strictly speaking, a fractal pattern) changes with the scale at which it is measured. It has also been characterized as a measure of the space-filling capacity of a pattern that tells how a fractal scales differently from the space it is embedded in; a fractal dimension does not have to be an integer. The essential idea of "fractured" dimensions has a long history in mathematics, but the term itself was brought to the fore by Benoit Mandelbrot based on his 1967 paper on self-similarity in which he discussed ''fractional dimensions''. In that paper, Mandelbrot cited previous work by Lewis Fry Richardson describing the counter-intuitive notion that a coastline's measured length changes with the length of the measuring stick used ( see Fig. 1). In terms of that notion, the fractal dimension of a coastline quantifies ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractal Analysis
Fractal analysis is assessing fractal characteristics of data. It consists of several methods to assign a fractal dimension and other fractal characteristics to a dataset which may be a theoretical dataset, or a pattern or signal extracted from phenomena including topography, natural geometric objects, ecology and aquatic sciences, sound, market fluctuations, heart rates, frequency domain in electroencephalography signals, digital images, molecular motion, and data science. Fractal analysis is now widely used in all areas of science. An important limitation of fractal analysis is that arriving at an empirically determined fractal dimension does not necessarily prove that a pattern is fractal; rather, other essential characteristics have to be considered. Fractal analysis is valuable in expanding our knowledge of the structure and function of various systems, and as a potential tool to mathematically assess novel areas of study. Fractal calculus was formulated which is a generaliz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Local Connected Dimension
Local may refer to: Geography and transportation * Local (train), a train serving local traffic demand * Local, Missouri, a community in the United States * Local government, a form of public administration, usually the lowest tier of administration * Local news, coverage of events in a local context which would not normally be of interest to those of other localities * Local union, a locally based trade union organization which forms part of a larger union Arts, entertainment, and media * ''Local'' (comics), a limited series comic book by Brian Wood and Ryan Kelly * ''Local'' (novel), a 2001 novel by Jaideep Varma * Local TV LLC, an American television broadcasting company * Locast, a non-profit streaming service offering local, over-the-air television * ''The Local'' (film), a 2008 action-drama film * '' The Local'', English-language news websites in several European countries Computing * .local, a network address component * Local variable, a variable that is given loca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multifractal Analysis
A multifractal system is a generalization of a fractal system in which a single exponent (the fractal dimension) is not enough to describe its dynamics; instead, a continuous spectrum of exponents (the so-called singularity spectrum) is needed. Multifractal systems are common in nature. They include the length of coastlines, mountain topography, fully developed turbulence, real-world scenes, heartbeat dynamics, human gait and activity, human brain activity, and natural luminosity time series. Models have been proposed in various contexts ranging from turbulence in fluid dynamics to internet traffic, finance, image modeling, texture synthesis, meteorology, geophysics and more. The origin of multifractality in sequential (time series) data has been attributed to mathematical convergence effects related to the central limit theorem that have as foci of convergence the family of statistical distributions known as the Tweedie exponential dispersion models, as well as the geometri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Section The Data
Section, Sectioning or Sectioned may refer to: Arts, entertainment and media * Section (music), a complete, but not independent, musical idea * Section (typography), a subdivision, especially of a chapter, in books and documents ** Section sign (§), typographical characters * Section (bookbinding), a group of sheets, folded in the middle, bound into the binding together * The Section (band), a 1970s American instrumental rock band * ''The Outpost'' (1995 film), also known as ''The Section'' * Section, an instrumental group within an orchestra * "Section", a song by 2 Chainz from the 2016 album ''ColleGrove'' * "Sectioning", a ''Peep Show'' episode * David "Section" Mason, a fictional character in '' Call of Duty: Black Ops II'' Organisations * Section (Alpine club) * Section (military unit) * Section (Scouting) Science, technology and mathematics Science * Section (archaeology), a view in part of the archaeological sequence showing it in the vertical plane * Section (bi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
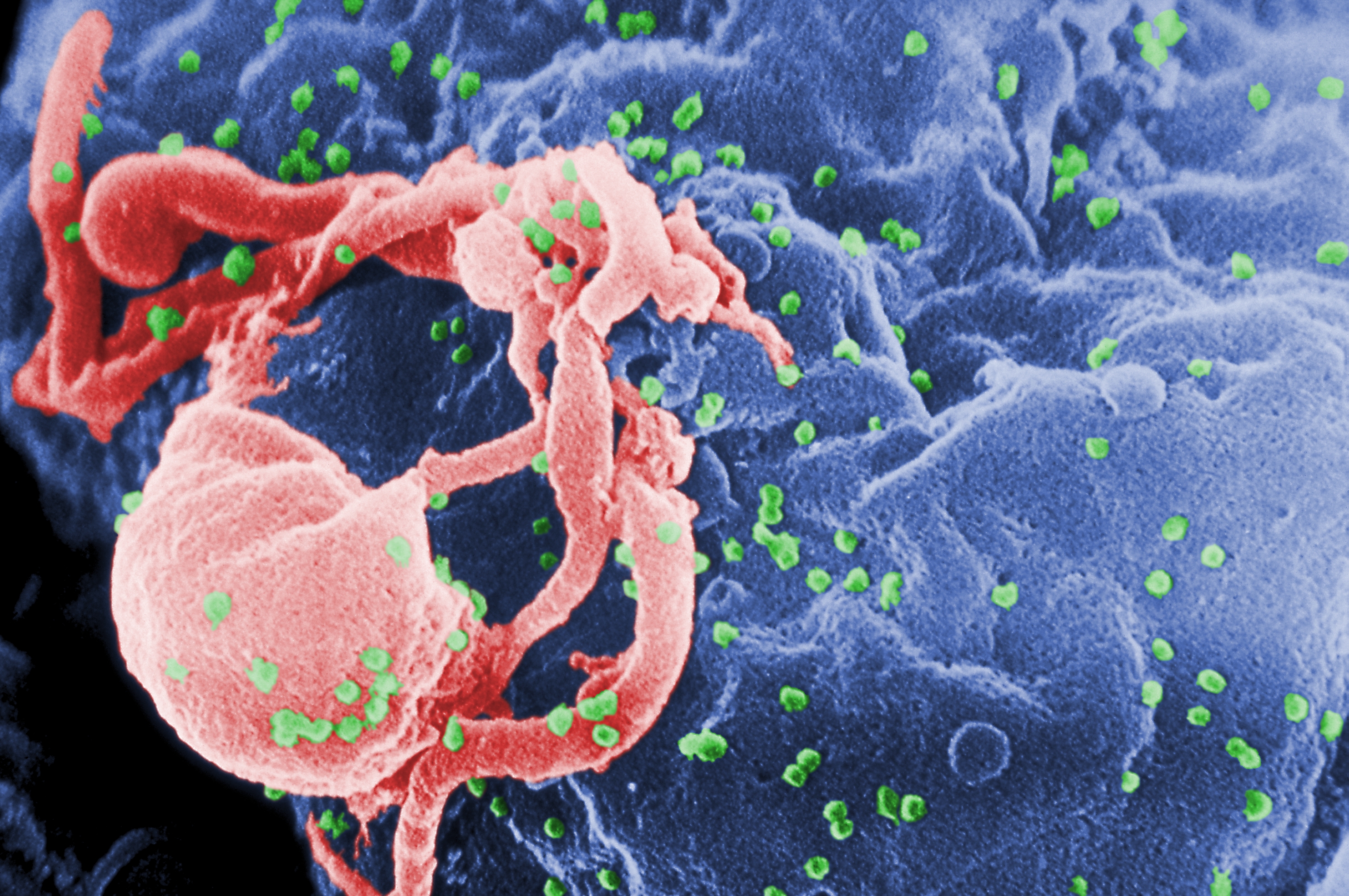
Grids
AIDS is caused by a human immunodeficiency virus (HIV), which originated in non-human primates in Central and West Africa. While various sub-groups of the virus acquired human infectivity at different times, the present pandemic had its origins in the emergence of one specific strain – HIV-1 subgroup M – in Léopoldville in the Belgian Congo (now Kinshasa in the Democratic Republic of the Congo) in the 1920s. There are two types of HIV: HIV-1 and HIV-2. HIV-1 is more virulent, easily transmitted and is the cause of the vast majority of HIV infections globally. The pandemic strain of HIV-1 is closely related to a virus found in chimpanzees of the subspecies ''Pan troglodytes troglodytes'', which live in the forests of the Central African nations of Cameroon, Equatorial Guinea, Gabon, the Republic of the Congo, and the Central African Republic. HIV-2 is less transmittable and is largely confined to West Africa, along with its closest relative, a virus of the sooty mangabey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |