 |
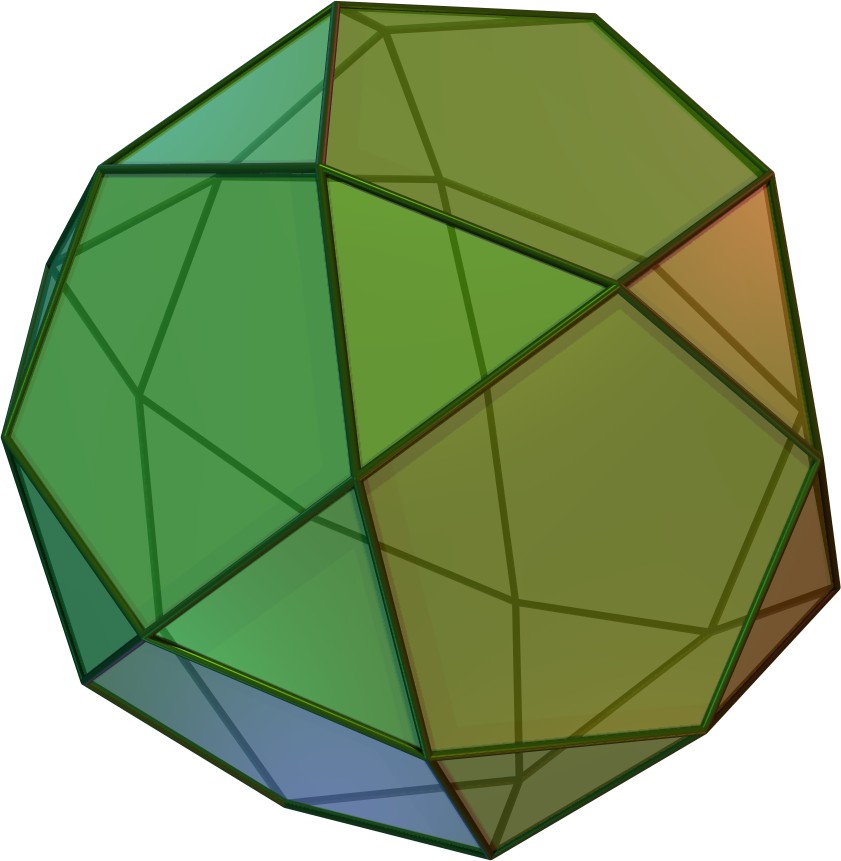
Birotunda
In geometry, a birotunda is any member of a family of dihedral-symmetric polyhedra, formed from two rotunda adjoined through the largest face. They are similar to a bicupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. There are two forms, ''ortho-'' and ''gyro-'': an ''orthobirotunda'' has one of the two rotundas is placed as the mirror reflection of the other, while in a ''gyrobirotunda'' one rotunda is twisted relative to the other. The pentagonal birotundas can be formed with regular faces, one a Johnson solid, the other a semiregular polyhedron: * pentagonal orthobirotunda, * pentagonal gyrobirotunda, which is also called an icosidodecahedron. Other forms can be generated with dihedral symmetry and distorted equilateral pentagons. Examples See also *Gyroelongated pentagonal birotunda *Elongated pentagonal orthobirotunda *Elongated pentagonal gyrobirotunda In geometry, the elongated pentagonal gyrobirotunda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Pentagonal Orthobirotunda
In geometry, the pentagonal orthobirotunda is one of the Johnson solids (). It can be constructed by joining two pentagonal rotundae () along their decagonal faces, matching like faces. Related polyhedra The pentagonal orthobirotunda is also related to an Archimedean solid, the icosidodecahedron, which can also be called a ''pentagonal gyrobirotunda'', similarly created by two pentagonal rotunda but with a 36-degree rotation Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional .... External links * Johnson solids {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Rotunda (geometry)
In geometry, a rotunda is any member of a family of dihedral-symmetric polyhedra. They are similar to a cupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. The pentagonal rotunda is a Johnson solid In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johns .... Other forms can be generated with dihedral symmetry and distorted equilateral pentagons. Examples Star-rotunda See also * Birotunda References * Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others. * The first proof that there are only 92 Johnson solids. {{Polyhedron navigator Johnson solids ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Johnson Solid
In geometry, a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides ( ); it has 1 square face and 4 triangular faces. Some authors require that the solid not be uniform (i.e., not Platonic solid, Archimedean solid, uniform prism, or uniform antiprism) before they refer to it as a “Johnson solid”. As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid () is an example that has a degree-5 vertex. Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the face ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pentagonal Orthobirotunda
In geometry, the pentagonal orthobirotunda is one of the Johnson solids (). It can be constructed by joining two pentagonal rotundae () along their decagonal faces, matching like faces. Related polyhedra The pentagonal orthobirotunda is also related to an Archimedean solid, the icosidodecahedron, which can also be called a ''pentagonal gyrobirotunda'', similarly created by two pentagonal rotunda but with a 36-degree rotation Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional .... External links * Johnson solids {{Polyhedron-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
List Of Spherical Symmetry Groups
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry. This article lists the groups by Schoenflies notation, Coxeter notation, orbifold notation, and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion. Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.Sands, 1993 Involutional symmetry There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Green Square Orthobirotunda
Green is the color between cyan and yellow on the visible spectrum. It is evoked by light which has a dominant wavelength of roughly 495570 nm. In subtractive color systems, used in painting and color printing, it is created by a combination of yellow and cyan; in the RGB color model, used on television and computer screens, it is one of the additive primary colors, along with red and blue, which are mixed in different combinations to create all other colors. By far the largest contributor to green in nature is chlorophyll, the chemical by which plants photosynthesize and convert sunlight into chemical energy. Many creatures have adapted to their green environments by taking on a green hue themselves as camouflage. Several minerals have a green color, including the emerald, which is colored green by its chromium content. During post-classical and early modern Europe, green was the color commonly associated with wealth, merchants, bankers, and the gentry, whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Square Gyrobirotunda
In Euclidean geometry, a square is a regular polygon, regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree (angle), degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose Internal and external angle, internal angle, central angle#Central angle of a regular polygon, central angle, and Internal and external angle, external angle are all equal (90°), and whose diagonals are all equal in length. A square with Vertex (geometry), vertices ''ABCD'' would be denoted . Characterizations A Convex polygon, convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Green Square Gyrobirotunda
Green is the color between cyan and yellow on the visible spectrum. It is evoked by light which has a dominant wavelength of roughly 495570 nm. In subtractive color systems, used in painting and color printing, it is created by a combination of yellow and cyan; in the RGB color model, used on television and computer screens, it is one of the additive primary colors, along with red and blue, which are mixed in different combinations to create all other colors. By far the largest contributor to green in nature is chlorophyll, the chemical by which plants photosynthesize and convert sunlight into chemical energy. Many creatures have adapted to their green environments by taking on a green hue themselves as camouflage. Several minerals have a green color, including the emerald, which is colored green by its chromium content. During post-classical and early modern Europe, green was the color commonly associated with wealth, merchants, bankers, and the gentry, while red ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Octagonal Orthobirotunda
In geometry, an octagon (from the Greek ὀκτάγωνον ''oktágōnon'', "eight angles") is an eight-sided polygon or 8-gon. A ''regular octagon'' has Schläfli symbol and can also be constructed as a quasiregular truncated square, t, which alternates two types of edges. A truncated octagon, t is a hexadecagon, . A 3D analog of the octagon can be the rhombicuboctahedron with the triangular faces on it like the replaced edges, if one considers the octagon to be a truncated square. Properties of the general octagon The sum of all the internal angles of any octagon is 1080°. As with all polygons, the external angles total 360°. If squares are constructed all internally or all externally on the sides of an octagon, then the midpoints of the segments connecting the centers of opposite squares form a quadrilateral that is both equidiagonal and orthodiagonal (that is, whose diagonals are equal in length and at right angles to each other).Dao Thanh Oai (2015), "Equilateral tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Green Octagonal Orthobirotunda
Green is the color between cyan and yellow on the visible spectrum. It is evoked by light which has a dominant wavelength of roughly 495570 nm. In subtractive color systems, used in painting and color printing, it is created by a combination of yellow and cyan; in the RGB color model, used on television and computer screens, it is one of the additive primary colors, along with red and blue, which are mixed in different combinations to create all other colors. By far the largest contributor to green in nature is chlorophyll, the chemical by which plants photosynthesize and convert sunlight into chemical energy. Many creatures have adapted to their green environments by taking on a green hue themselves as camouflage. Several minerals have a green color, including the emerald, which is colored green by its chromium content. During post-classical and early modern Europe, green was the color commonly associated with wealth, merchants, bankers, and the gentry, while red was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Heptagonal Orthobirotunda
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon. The heptagon is sometimes referred to as the septagon, using "sept-" (an elision of ''septua-'', a Latin-derived numerical prefix, rather than ''hepta-'', a Greek-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle. Regular heptagon A regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128 degrees). Its Schläfli symbol is . Area The area (''A'') of a regular heptagon of side length ''a'' is given by: :A = \fraca^2 \cot \frac \simeq 3.634 a^2. This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of \pi/7, and the area of each of the 14 small triangles is one-fourth of the apothem. The area of a regular heptagon i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |