|
Biological Applications Of Bifurcation Theory
Biological applications of bifurcation theory provide a framework for understanding the behavior of biological networks modeled as dynamical systems. In the context of a biological system, bifurcation theory describes how small changes in an input parameter can cause a bifurcation or qualitative change in the behavior of the system. The ability to make dramatic change in system output is often essential to organism function, and bifurcations are therefore ubiquitous in biological networks such as the switches of the cell cycle. Biological networks and dynamical systems Biological networks originate from evolution and therefore have less standardized components and potentially more complex interactions than networks designed by humans, such as electrical networks. At the cellular level, components of a network can include a large variety of proteins, many of which differ between organisms. Network interactions occur when one or more proteins affect the function of another through tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical System
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, fluid dynamics, the flow of water in a pipe, the Brownian motion, random motion of particles in the air, and population dynamics, the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real number, real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a Set (mathematics), set, without the need of a Differentiability, smooth space-time structure defined on it. At any given time, a dynamical system has a State ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrasensitivity
In molecular biology, ultrasensitivity describes an output response that is more sensitive to stimulus change than the hyperbolic Michaelis-Menten response. Ultrasensitivity is one of the biochemical switches in the cell cycle and has been implicated in a number of important cellular events, including exiting G2 cell cycle arrests in ''Xenopus laevis'' oocytes, a stage to which the cell or organism would not want to return. Ultrasensitivity is a cellular system which triggers entry into a different cellular state. Ultrasensitivity gives a small response to first input signal, but an increase in the input signal produces higher and higher levels of output. This acts to filter out noise, as small stimuli and threshold concentrations of the stimulus (input signal) is necessary for the trigger which allows the system to get activated quickly. Ultrasensitive responses are represented by sigmoidal graphs, which resemble cooperativity. The quantification of ultrasensitivity is often perfo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Formula
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, grouping, AC method), completing the square, graphing and others. Given a general quadratic equation of the form :ax^2+bx+c=0 with representing an unknown, with , and representing constants, and with , the quadratic formula is: :x = \frac where the plus–minus symbol "±" indicates that the quadratic equation has two solutions. Written separately, they become: : x_1=\frac\quad\text\quad x_2=\frac Each of these two solutions is also called a root (or zero) of the quadratic equation. Geometrically, these roots represent the -values at which ''any'' parabola, explicitly given as , crosses the -axis. As well as being a formula that yields the zeros of any parabola, the quadratic formula can also be used to identify the axis of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Stability
In mathematics, in the theory of differential equations and dynamical systems, a particular stationary or quasistationary solution to a nonlinear system is called linearly unstable if the linearization of the equation at this solution has the form \frac = A r, where ''r'' is the perturbation to the steady state, ''A'' is a linear operator whose spectrum contains eigenvalues with ''positive'' real part. If all the eigenvalues have ''negative'' real part, then the solution is called linearly stable. Other names for linear stability include exponential stability or stability in terms of first approximation. If there exist an eigenvalue with ''zero'' real part then the question about stability cannot be solved on the basis of the first approximation and we approach the so-called "centre and focus problem". Examples Ordinary differential equation The differential equation \frac = x - x^2 has two stationary (time-independent) solutions: ''x'' = 0 and ''x'' = 1. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imperfect Transcritical
The imperfect (abbreviated ) is a verb form that combines past tense (reference to a past time) and imperfective aspect (reference to a continuing or repeated event or state). It can have meanings similar to the English "was walking" or "used to walk". It contrasts with preterite forms, which refer to a single completed event in the past. Traditionally, the imperfect of languages such as Latin and French is referred to as one of the tenses, although it actually encodes aspectual information in addition to tense (time reference). It may be more precisely called ''past imperfective''. English has no general imperfective and expresses it in different ways. The term "imperfect" in English refers to forms much more commonly called ''past progressive'' or ''past continuous'' (e.g. "was doing" or "were doing"). These are combinations of past tense with specifically continuous or progressive aspect. In German, formerly referred to the simply conjugated past tense (to contrast with the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Transcritical
Perfect commonly refers to: * Perfection, completeness, excellence * Perfect (grammar), a grammatical category in some languages Perfect may also refer to: Film * ''Perfect'' (1985 film), a romantic drama * ''Perfect'' (2018 film), a science fiction thriller Literature * ''Perfect'' (Friend novel), a 2004 novel by Natasha Friend * ''Perfect'' (Hopkins novel), a young adult novel by Ellen Hopkins * ''Perfect'' (Joyce novel), a 2013 novel by Rachel Joyce * ''Perfect'' (Shepard novel), a Pretty Little Liars novel by Sara Shepard * ''Perfect'', a young adult science fiction novel by Dyan Sheldon Music * Perfect interval, in music theory * Perfect Records, a record label Artists * Perfect (musician) (born 1980), reggae singer * Perfect (Polish band) * Perfect (American band), an American alternative rock group Albums * ''Perfect'' (Intwine album) (2004) * ''Perfect'' (Half Japanese album) (2016) * ''perfecT'', an album by Sam Shaber * ''Perfect'', an album by True Fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
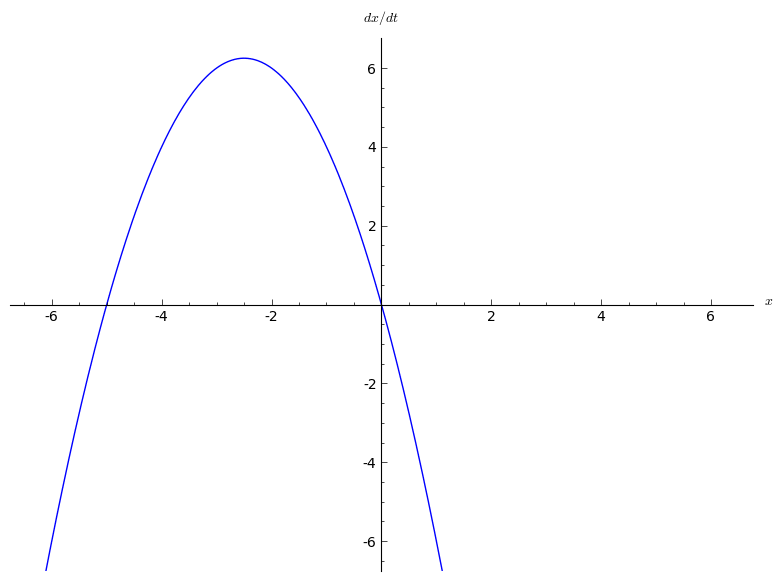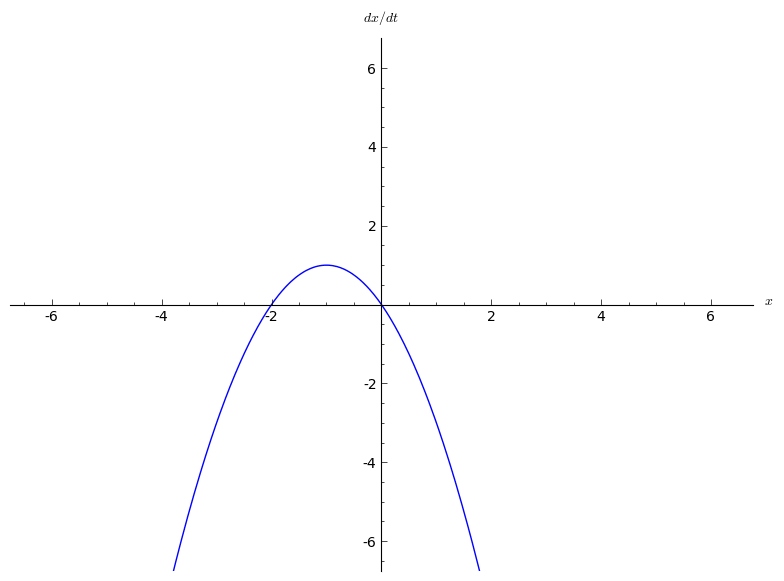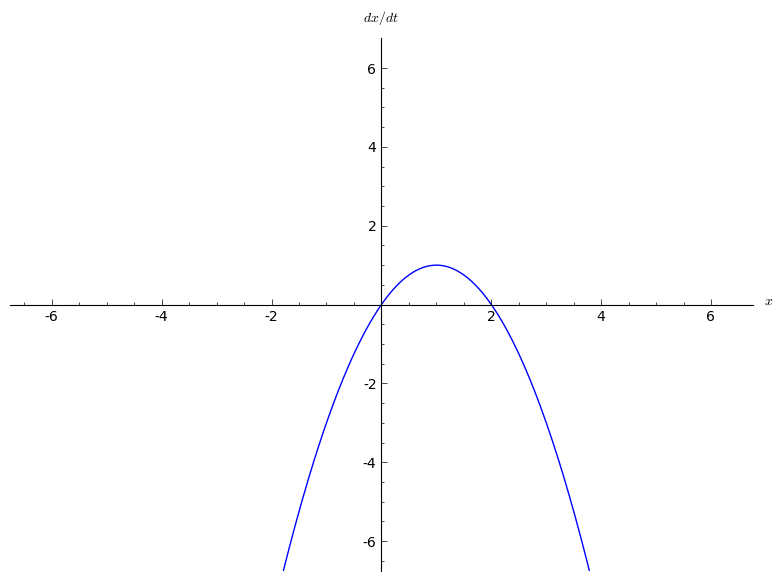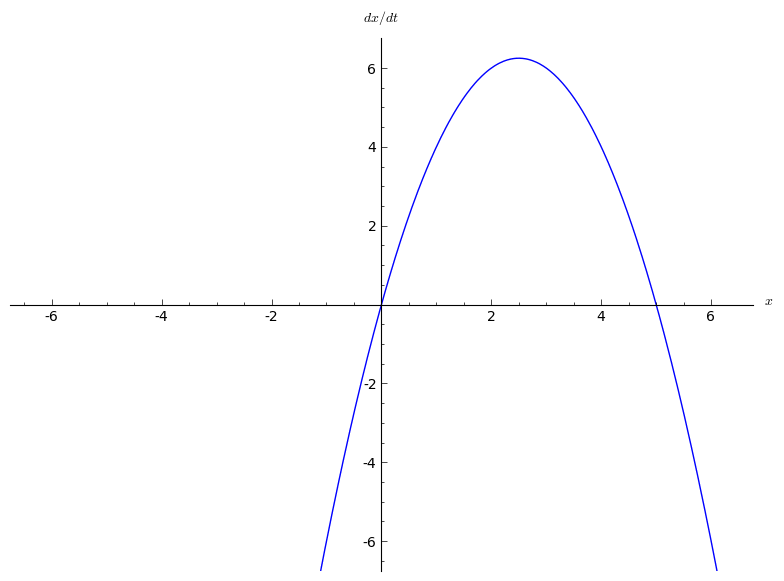
Transcritical Bifurcation
In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero. A transcritical bifurcation is one in which a fixed point exists for all values of a parameter and is never destroyed. However, such a fixed point interchanges its stability with another fixed point as the parameter is varied. In other words, both before and after the bifurcation, there is one unstable and one stable fixed point. However, their stability is exchanged when they collide. So the unstable fixed point becomes stable and vice versa. The normal form of a transcritical bifurcation is :\frac = rx - x^2. This equation is similar to the logistic equation A logistic function or logistic curve is a common S-shaped curve (sigmoid curve) with equation f(x) = \frac, where For values of x in the domain of real numbers from -\infty to +\inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic
Stochastic (, ) refers to the property of being well described by a random probability distribution. Although stochasticity and randomness are distinct in that the former refers to a modeling approach and the latter refers to phenomena themselves, these two terms are often used synonymously. Furthermore, in probability theory, the formal concept of a ''stochastic process'' is also referred to as a ''random process''. Stochasticity is used in many different fields, including the natural sciences such as biology, chemistry, ecology, neuroscience, and physics, as well as technology and engineering fields such as image processing, signal processing, information theory, computer science, cryptography, and telecommunications. It is also used in finance, due to seemingly random changes in financial markets as well as in medicine, linguistics, music, media, colour theory, botany, manufacturing, and geomorphology. Etymology The word ''stochastic'' in English was originally used as a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Point
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematics, mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by Ordinary differential equation, ordinary, Delay differential equation, delay or Partial differential equation, partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them . Bif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-point iter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
