|
Burmester Theory
In kinematics, Burmester theory comprises geometric techniques for synthesis of linkages. It was introduced in the late 19th century by Ludwig Burmester (1840–1927). His approach was to compute the geometric constraints of the linkage directly from the inventor's desired movement for a floating link. From this point of view a four-bar linkage is a floating link that has two points constrained to lie on two circles. Burmester began with a set of locations, often called ''poses'', for the floating link, which are viewed as snapshots of the constrained movement of this floating link in the device that is to be designed. The design of a crank for the linkage now becomes finding a point in the moving floating link that when viewed in each of these specified positions has a trajectory that lies on a circle. The dimension of the crank is the distance from the point in the floating link, called the circling point, to the center of the circle it travels on, called the center point. Two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematics
Kinematics is a subfield of physics, developed in classical mechanics, that describes the Motion (physics), motion of points, Physical object, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics (physics), kinetics, not kinematics. For further details, see analytical dynamics. Kinematics is used in astrophysics to describe the motion of celestial bodies and collections of such bodies. In mechanical engin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linkage (mechanical)
A mechanical linkage is an assembly of systems connected to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for example, and are called joints. A linkage modeled as a network of rigid links and ideal joints is called a kinematic chain. Linkages may be constructed from open chains, closed chains, or a combination of open and closed chains. Each link in a chain is connected by a joint to one or more other links. Thus, a kinematic chain can be modeled as a graph in which the links are paths and the joints are vertices, which is called a linkage graph. The movement of an ideal joint is generally associated with a subgroup of the group of Euclidean displacements. The number of parameters in the subgroup is called the degrees of freedom (DOF) of the joint. Mechanical linkages are usually designed to tra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludwig Burmester
Ludwig Ernst Hans Burmester (5 May 1840 – 20 April 1927) was a German kinematician and geometer. His doctoral thesis (from German: ''About the elements of a theory of isophotes'') concerned lines on a surface defined by light direction. After a period as a teacher in Łódź he became professor of synthetic geometry at Dresden where his growing interest in kinematics culminated in his (''Textbook of Kinematics, First Volume, Planar Motion'') of 1888, developing the approach to the theory of linkages introduced by Franz Reuleaux, whereby a planar mechanism was understood as a collection of Euclidean planes in relative motion with one degree of freedom. Burmester considered both the theory of planar kinematics and practically all actual mechanisms known in his time. In doing so, Burmester developed Burmester theory which applies projective geometry to the loci of points on planes moving in straight lines and in circles, where any motion may be understood in relation to four Bur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Four-bar Linkage
In the study of mechanisms, a four-bar linkage, also called a four-bar, is the simplest closed- chain movable linkage. It consists of four bodies, called ''bars'' or ''links'', connected in a loop by four joints. Generally, the joints are configured so the links move in parallel planes, and the assembly is called a ''planar four-bar linkage''. Spherical and spatial four-bar linkages also exist and are used in practice. Planar four-bar linkage Planar four-bar linkages are constructed from four links connected in a loop by four one- degree-of-freedom joints. A joint may be either a revolute joint – also known as a pin joint or hinged joint – denoted by R, or a prismatic joint – also known as a sliding pair – denoted by P. A link that are fixed in place relative to the viewer is called a ''ground link.'' A link connecting to the ground by a revolute joint that can perform a complete revolution is called a '' crank link.'' A link connecting to the ground by a revolute join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crank (mechanism)
A crank is an arm attached at a right angle to a rotating shaft by which circular motion is imparted to or received from the shaft. When combined with a connecting rod, it can be used to convert circular motion into reciprocating motion, or vice versa. The arm may be a bent portion of the shaft, or a separate arm or disk attached to it. Attached to the end of the crank by a pivot is a rod, usually called a connecting rod (conrod). The term often refers to a human-powered crank which is used to manually turn an axle, as in a bicycle crankset or a brace and bit drill. In this case a person's arm or leg serves as the connecting rod, applying reciprocating force to the crank. There is usually a bar perpendicular to the other end of the arm, often with a freely rotatable handle or pedal attached. Examples Familiar examples include: Hand-powered cranks * Spinning Wheel * Mechanical pencil sharpener * Fishing reel and other reels for cables, wires, ropes, etc. *Starting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete trajectory is defined by position and momentum, simultaneously. The mass might be a projectile or a satellite. For example, it can be an orbit — the path of a planet, asteroid, or comet as it travels around a central mass. In control theory, a trajectory is a time-ordered set of states of a dynamical system (see e.g. Poincaré map). In discrete mathematics, a trajectory is a sequence (f^k(x))_ of values calculated by the iterated application of a mapping f to an element x of its source. Physics of trajectories A familiar example of a trajectory is the path of a projectile, such as a thrown ball or rock. In a significantly simplified model, the object moves only under the influence of a uniform gravitational force field. This can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instant Centre Of Rotation
The instant center of rotation (also, instantaneous velocity center, instantaneous center, or instant center) is the point fixed to a body undergoing planar movement that has zero velocity at a particular instant of time. At this instant, the velocity vectors of the other points in the body generate a circular field around this point which is identical to what is generated by a pure rotation. Planar movement of a body is often described using a plane figure moving in a two-dimensional plane. The instant center is the point in the moving plane around which all other points are rotating at a specific instant of time. The continuous movement of a plane has an instant center for every value of the time parameter. This generates a curve called the moving centrode. The points in the fixed plane corresponding to these instant centers form the fixed centrode. The generalization of this concept to 3-dimensional space is that of a twist around a screw. The screw has an axis which is a l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation : applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an equation. Here is a non-zero linear combination of the third-degree monomials : These are ten in number; therefore the cubic curves form a projective space of dimension 9, over any given field . Each point imposes a single linear condition on , if we ask that pass through . Therefore, we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position; compare to two points determining a line and how five points determine a conic. If two cubics pass through a given set of nine points, then in fact a pencil of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem. A cubic curve may have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
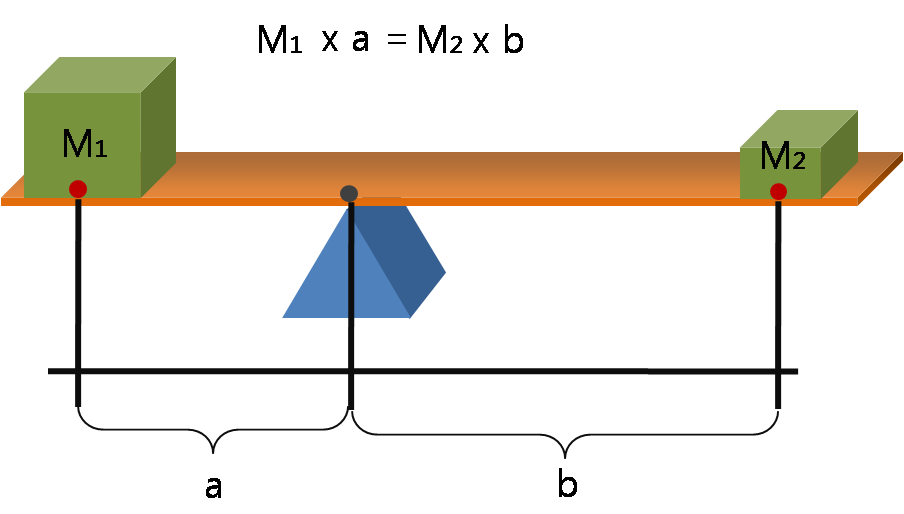
Levers
A lever is a simple machine consisting of a beam or rigid rod pivoted at a fixed hinge, or ''fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load and effort, the lever is divided into three types. Also, leverage is mechanical advantage gained in a system. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage. The ratio of the output force to the input force is the mechanical advantage of the lever. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English around 1300 from Old French, in which the word was ''levier''. This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to the Latin ''levare'', itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hinged
A hinge is a mechanical bearing that connects two solid objects, typically allowing only a limited angle of rotation between them. Two objects connected by an ideal hinge rotate relative to each other about a fixed axis of rotation: all other translations or rotations being prevented, and thus a hinge has one degree of freedom. Hinges may be made of flexible material or of moving components. In biology, many joints function as hinges, like the elbow joint. History Ancient remains of stone, marble, wood, and bronze hinges have been found. Some date back to at least Ancient Egypt. In Ancient Rome, hinges were called cardō and gave name to the goddess Cardea and the main street Cardo. This name cardō lives on figuratively today as "the chief thing (on which something turns or depends)" in words such as ''cardinal''. According to the OED, the English word hinge is related to ''hang''. Door hinges ; Barrel hinge: A barrel hinge consists of a sectional barrel (the knuckle) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)



.gif)