|
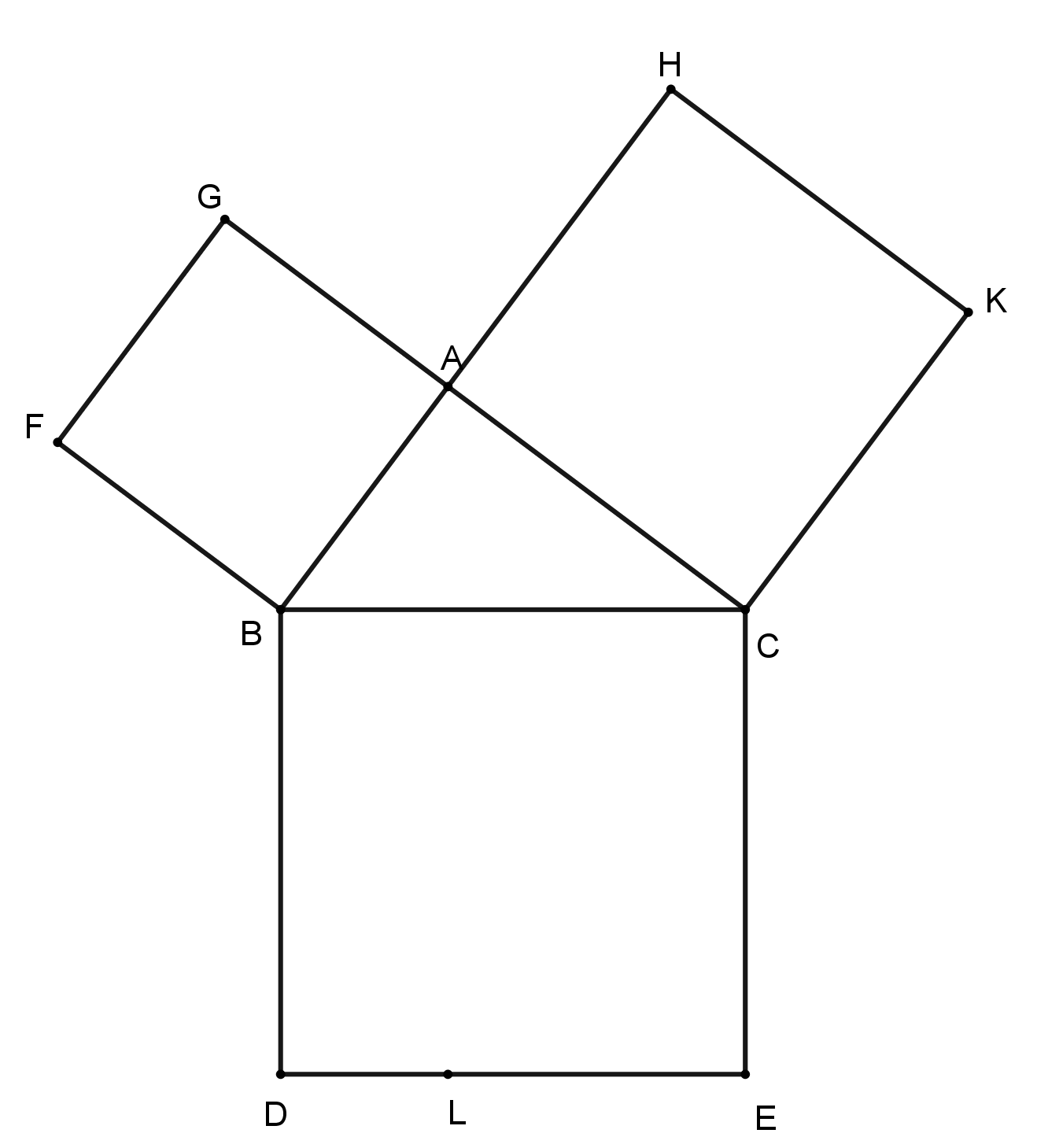
Bride's Chair
In geometry, a Bride's Chair is an illustration of the Pythagorean theorem. The figure appears in Proposition 47 of Book I of Euclid's Elements. It is also known by several other names, such as the Franciscan's cowl, peacock's tail, windmill, Pythagorean pants, Figure of the Bride, theorem of the married women, and chase of the little married women. According to Swiss-American historian of mathematics Florian Cajori, the ultimate etymology of the term "Bride's Chair" lies in a Greek homonym: "Some Arabic writers [...] call the Pythagorean theorem 'figure of the bride'." The Greek word has two relevant definitions: 'bride', and 'winged insect'. The figure of a right triangle with the three squares has reminded various writers of an insect, so the 'insect' sense of the Greek word came to be applied to right triangles with three squares, and to the Pythagorean theorem. Arabic speakers writing in Greek would often mistakenly assume the other sense of the word was intended, and would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brides Chair 02
A bride is a woman who is about to be married or who is newlywed. When marrying, the bride's future spouse, (if male) is usually referred to as the ''bridegroom'' or just ''groom''. In Western culture, a bride may be attended by a maid, bridesman and one or more bridesmaids. Etymology The word comes from the Old English 'bryd', a word shared with other Germanic languages. Its further origin is unknown. Attire In Europe and North America, the typical attire for a bride is a formal dress, and a veil. Usually, in the "white wedding" model, the bride's dress is bought specifically for the wedding, and is not in a style that could be worn for any subsequent events. Previously, until at least the middle of the 19th century, the bride generally wore her best dress, whatever color it was, or if the bride was well-off, she ordered a new dress in her favorite color and expected to wear it again. For first marriages in Western countries, a white wedding dress is usually worn, a tradi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclid's Elements
The ''Elements'' ( grc, Στοιχεῖα ''Stoikheîa'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postulates, propositions ( theorems and constructions), and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. ''Elements'' is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century. Euclid's ''Elements'' has been referred to as the most successful and influential textbook ever written. It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Florian Cajori
Florian Cajori (February 28, 1859 – August 14 or 15, 1930) was a Swiss-American historian of mathematics. Biography Florian Cajori was born in Zillis, Switzerland, as the son of Georg Cajori and Catherine Camenisch. He attended schools first in Zillis and later in Chur. In 1875, Florian Cajori emigrated to the United States at the age of sixteen, and attended the State Normal school in Whitewater, Wisconsin. After graduating in 1878, he taught in a country school, and then later began studying mathematics at University of Wisconsin–Madison. In 1883, Cajori received both his bachelor's and master's degrees from the University of Wisconsin–Madison, briefly attended Johns Hopkins University for 8 months in between degrees. He taught for a few years at Tulane University, before being appointed as professor of applied mathematics there in 1887. He was then driven north by tuberculosis. He founded the Colorado College Scientific Society and taught at Colorado College wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homonym
In linguistics, homonyms are words which are homographs (words that share the same spelling, regardless of pronunciation), or homophones (equivocal words, that share the same pronunciation, regardless of spelling), or both. Using this definition, the words ''row'' (propel with oars), ''row'' (a linear arrangement) and ''row'' (an argument) are homonyms because they are homographs (though only the first two are homophones): so are the words ''see'' (vision) and ''sea'' (body of water), because they are homophones (though not homographs). A more restrictive and technical definition requires that homonyms be simultaneously homographs ''and'' homophoneshomonym ''Random House Unabridged Dictionary'' at dictionary.com – that is to say they have identical spelling ''and'' pronunciation, but with different meanings. Examples are the pair ''stalk'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Schopenhauer
Arthur Schopenhauer ( , ; 22 February 1788 – 21 September 1860) was a German philosopher. He is best known for his 1818 work '' The World as Will and Representation'' (expanded in 1844), which characterizes the phenomenal world as the product of a blind noumenal will. Building on the transcendental idealism of Immanuel Kant (1724–1804), Schopenhauer developed an atheistic metaphysical and ethical system that rejected the contemporaneous ideas of German idealism. He was among the first thinkers in Western philosophy to share and affirm significant tenets of Indian philosophy, such as asceticism, denial of the self, and the notion of the world-as-appearance. His work has been described as an exemplary manifestation of philosophical pessimism. Though his work failed to garner substantial attention during his lifetime, Schopenhauer had a posthumous impact across various disciplines, including philosophy, literature, and science. His writing on aesthetics, morality ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Illustration To Euclid's Proof Of The Pythagorean Theorem2
An illustration is a decoration, interpretation or visual explanation of a text, concept or process, designed for integration in print and digital published media, such as posters, flyers, magazines, books, teaching materials, animations, video games and films. An illustration is typically created by an illustrator. Digital illustrations are often used to make websites and apps more user-friendly, such as the use of emojis to accompany digital type. llustration also means providing an example; either in writing or in picture form. The origin of the word "illustration" is late Middle English (in the sense ‘illumination; spiritual or intellectual enlightenment’): via Old French from Latin ''illustratio''(n-), from the verb ''illustrare''. Illustration styles Contemporary illustration uses a wide range of styles and techniques, including drawing, painting, printmaking, collage, montage, digital design, multimedia, 3D modelling. Depending on the purpose, illustration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (geometry)
In geometry, a line is an infinitely long object with no width, depth, or curvature. Thus, lines are one-dimensional objects, though they may exist in two, three, or higher dimension spaces. The word ''line'' may also refer to a line segment in everyday life, which has two points to denote its ends. Lines can be referred by two points that lay on it (e.g., \overleftrightarrow) or by a single letter (e.g., \ell). Euclid described a line as "breadthless length" which "lies evenly with respect to the points on itself"; he introduced several postulates as basic unprovable properties from which he constructed all of geometry, which is now called Euclidean geometry to avoid confusion with other geometries which have been introduced since the end of the 19th century (such as non-Euclidean, projective and affine geometry). In modern mathematics, given the multitude of geometries, the concept of a line is closely tied to the way the geometry is described. For instance, in analy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hsuan Thu
Xuan tu or Hsuan thu () is a diagram given in the ancient Chinese astronomical and mathematical text ''Zhoubi Suanjing'' indicating a proof of the Pythagorean theorem. ''Zhoubi Suanjing'' is one of the oldest Chinese texts on mathematics. The exact date of composition of the book has not been determined. Some estimates of the date range as far back as 1100 BCE, while others estimate the date as late as 200 CE. However, from astronomical evidence available in the book it would appear that much of the material in the book is from the time of Confucius Confucius ( ; zh, s=, p=Kǒng Fūzǐ, "Master Kǒng"; or commonly zh, s=, p=Kǒngzǐ, labels=no; – ) was a Chinese philosopher and politician of the Spring and Autumn period who is traditionally considered the paragon of Chinese sages. C ..., that is, the 6th century BCE. Hsuan thu represents one of the earliest known proofs of the Pythagorean theorem and also one of the simplest. The text in ''Zhoubi Suanjing'' accompanying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |